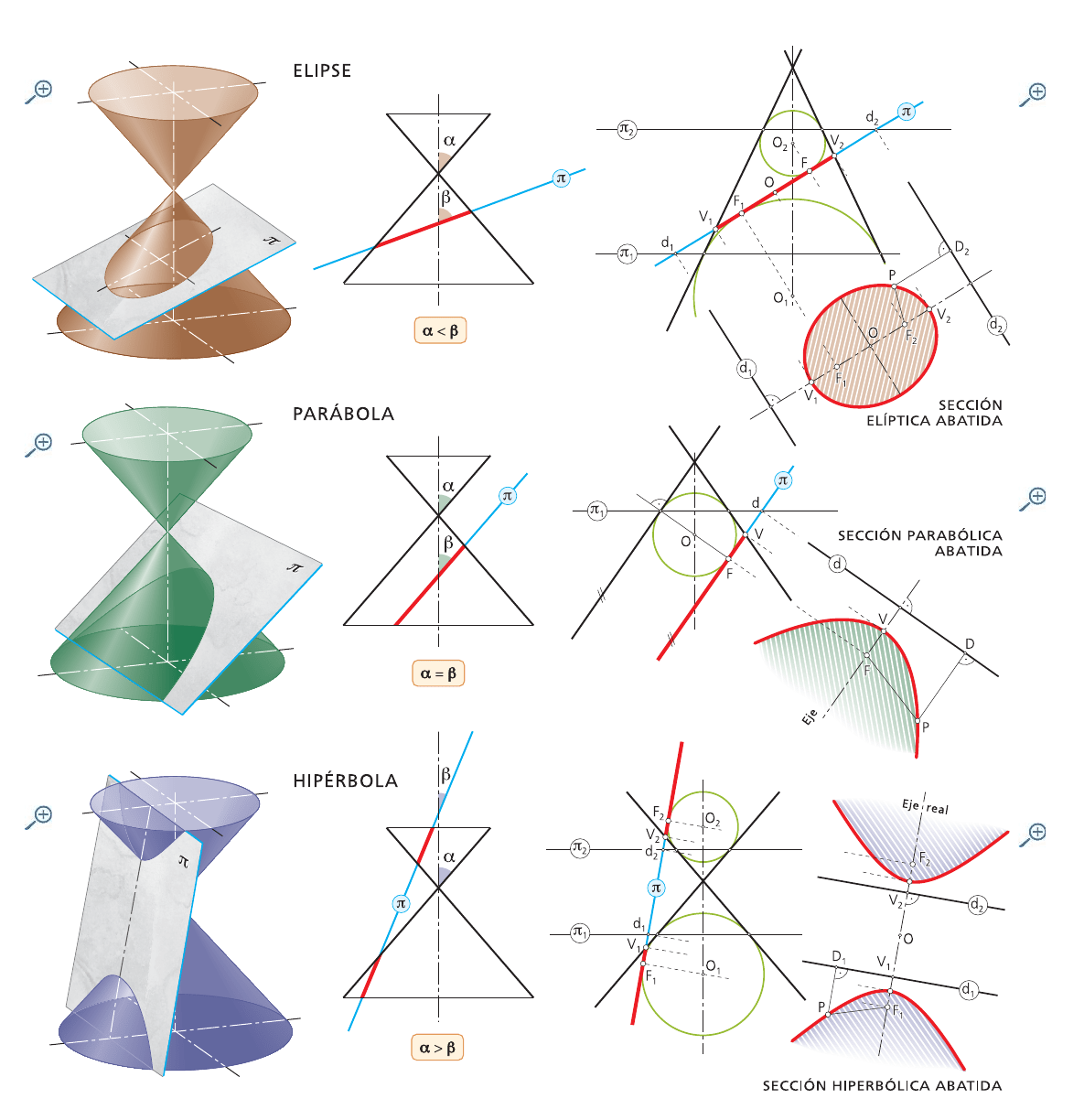
Tabla de contenidos

1. Curvas cónicas. Propiedades y métodos de construcción. La elipse.

TEOREMA DE DANDELÍN APLICADO A LA ELIPSE

• 1.1. Construcción de la elipse dados los ejes por el método de puntos.
• 1.2. Construcción de una elipse conocidos los ejes por afinidad con la circunferencia.
• 1.3. Trazado de elipse por intersección de rectas o haces proyectivos.
• 1.4. Trazado de una elipse dada por dos diámetros conjugados. Método 1.
• 1.5. Trazado de una elipse dada por dos diámetros conjugados. Método 2.
• 1.6. Trazado de los ejes reales de la elipse dada la curva.
• 1.7. Trazado de los ejes de una elipse a partir de dos diámetros conjugados.

2. Curvas cónicas. Propiedades y métodos de construcción. La hipérbola.

TEOREMA DE DANDELÍN APLICADO A LA HIPÉRBOLA

• 2.1. Construcción de la hipérbola dados los focos y los vértices. Método por puntos.
• 2.2. Construcción de la hipérbola dados un foco, el centro y un punto de la curva.
• 2.3. Trazado de una hipérbola conocidos un foco, el vértice opuesto a ese foco y un punto de la curva. Método de haces proyectivos.
• 2.4. Construir una hipérbola dados sus vértices y asíntotas. Método 1 (A partir de los focos y por puntos).
• 2.5. Construcción de la hipérbola a partir de los vértices y las asíntotas. Método 2 (Por paralelas a las asíntotas).
• 2.6. Construir una hipérbola dado un foco, un vértice y un punto de la curva.
• 2.7. Construir una hipérbola equilátera dado un punto de la curva y sus asíntotas.
• 2.8. Construir una hipérbola conociendo un foco, el centro y un punto de la curva.
• 2.9. Construir una hipérbola conociendo el eje real, el centro y una tangente.
• 2.10. Construir una hipérbola conocido el eje real, el centro y dos tangentes.
• 2.11. Construir una hipérbola dados un foco y tres tangentes.
• 2.12. Construir una hipérbola conociendo la longitud del eje real, un foco, una tangente y su punto de contacto.
• 2.13. Construir una hipérbola conociendo los focos y una tangente.
• 2.14. Construir una hipérbola conocido el radio de la circunferencia focal un foco y una asíntota.
• 2.15. Construir una hipérbola dados un foco, la directriz correspondiente y la excentricidad. Método directo.

3. Curvas cónicas. Propiedades y métodos de construcción. La parábola.

TEOREMA DE DANDELÍN APLICADO A LA PARÁBOLA

• 3.1. Construcción de la parábola por puntos de intersección de circunferencias concéntricas al foco y paralelas a la directriz.
• 3.2. Construcción de la parábola por semicircunferencias.
• 3.3. Construcción de la parábola conocido el eje, el vértice y un punto de la curva. Método 1.
• 3.4. Construcción de la parábola conocido el eje, el vértice y un punto de la curva. Método 2.
• 3.5. Construcción de la parábola conocida la directriz y dos puntos de la curva.
• 3.6. Construcción de la parábola conocido el foco y dos puntos de la curva.
• 3.7. Construcción de la parábola conocida la tangente en el vértice y dos tangentes a la curva.
• 3.8. Construcción de la parábola conocida la directriz, un punto de la curva y una recta tangente a ésta.
• 3.9. Construcción de la parábola conocida la directriz y dos tangentes a la curva.
• 3.10. Construcción de la parábola conocidas dos rectas tangentes a ésta y sus puntos de tangencia.
• 3.11. Construcción de la parábola conocido el foco, el eje de la curva y una recta tangente a ésta.
• 3.12. Construcción de la parábola conocido el foco, un punto de la curva y una recta tangente a ésta.
• 3.13. Construcción de la parábola conocido el foco y dos tangentes a la curva.
• 3.14. Enlazar dos rectas entre dos puntos marcados en ambas.

4. Tangentes, normales y recta secante a las curvas cónicas. La elipse.

• 4.1. CONCEPTOS SOBRE LA ELIPSE Y LAS TANGENCIAS.
• 4.2. RECTAS TANGENTE Y NORMAL A ELIPSE EN UN PUNTO P DE LA CURVA (CF).
• 4.3. RECTA TANGENTE A UNA ELIPSE EN UN PUNTO P DE LA CURVA (CP).
• 4.4. RECTAS TANGENTE Y NORMAL A ELIPSE EN UN PUNTO P DE LA CURVA (RV).
• 4.5. RECTAS TANGENTES A UNA ELIPSE DESDE UN PUNTO P EXTERIOR A LA CURVA (CF).
• 4.6. RECTAS TANGENTES A UNA ELIPSE DESDE UN PUNTO P EXTERIOR A LA CURVA (CP).
• 4.7. RECTAS TANGENTES A UNA ELIPSE PARALELAS A UNA RECTA O DIRECCIÓN CONOCIDA (CF).
• 4.8. RECTAS TANGENTES A UNA ELIPSE, PARALELAS A UNA RECTA O DIRECCIÓN CONOCIDA (CP).
• 4.9. RECTA SECANTE A UNA ELIPSE.

5. Tangentes, normales y recta secante a las curvas cónicas. La hipérbola.

• 5.1. RECTA TANGENTE A UNA HIPÉRBOLA EN UN PUNTO DE LA CURVA (CF).
• 5.2. RECTA TANGENTE A UNA HIPÉRBOLA EN UN PUNTO DE LA CURVA (CP).
• 5.3. RECTAS TANGENTES A UNA HIPÉRBOLA DESDE UN PUNTO P EXTERIOR A LA CURVA (CF).
• 5.4. RECTAS TANGENTES A UNA HIPÉRBOLA DESDE UN PUNTO P EXTERIOR A LA CURVA (CP).
• 5.5. RECTAS TANGENTES A UNA HIPÉRBOLA PARALELAS A UNA RECTA O DIRECCIÓN CONOCIDA (CF).
• 5.6. RECTAS TANGENTES A UNA HIPÉRBOLA PARALELAS A UNA RECTA O DIRECCIÓN CONOCIDA (CP).
• 5.7. RECTA SECANTE A UNA HIPÉRBOLA.

6. Tangentes, normales y recta secante a las curvas cónicas. La parábola.

• 6.1. RECTA TANGENTE A UNA PARÁBOLA EN UN PUNTO DE LA CURVA (CF).
• 6.2. RECTA TANGENTE A UNA PARÁBOLA EN UN PUNTO DE LA CURVA (CP).
• 6.3. RECTAS TANGENTES A UNA PARÁBOLA DESDE UN PUNTO P EXTERIOR A LA CURVA (CF).
• 6.4. RECTAS TANGENTES A UNA PARÁBOLA DESDE UN PUNTO P EXTERIOR A LA CURVA (CP).
• 6.5. RECTA TANGENTE A UNA PARÁBOLA PARALELA A UNA RECTA O DIRECCIÓN CONOCIDA (CF).
• 6.6. RECTA TANGENTE A UNA PARÁBOLA PARALELA A UNA RECTA O DIRECCIÓN CONOCIDA (CP).
• 6.7. RECTA SECANTE A UNA PARÁBOLA.