Fórmula de Euler para poliedros
Leonhard Euler fue un célebre matemático y físico nacido en Basilea (Suiza) un 15 de abril de 1707. Considerado entre los cinco mejores de la historia, su formidable trabajo derivó en aportaciones fundamentales a campos como la teoría de números, series infinitas, logaritmos, variable compleja, álgebra, geometría, combinatoria o la teoría de grafos. También publicó infinidad de estudios sobre hidrodinámica, mecánica, astronomía, óptica, ingeniería naval, … al tiempo que reformó y estableció nuevas formas de notación matemática aún vigentes en la actualidad.
Con tan solo 23 años, fue nombrado catedrático de Física, y tres años después, de Matemáticas. Euler fue un luchador innato, ya que antes de cumplir los treinta, comenzó a perder la vista de manera progresiva, hasta que se quedó casi ciego al final de su vida. Sin embargo, esto no le impidió tener una mente privilegiada para la investigación. Enormemente productivo, escribió libros de altísima calidad científica y de un tamaño considerable. Dentro de su legado podemos encontrar una gran variedad de aportaciones a las matemáticas, tales como fórmulas, polinomios, constantes o las líneas de Euler. Las integrales eulerianas, de gran actualidad en investigación y la introducción del símbolo e como base del logaritmo neperiano, son otros dos de sus logros. En 1736, fue capaz de resolver el llamado «problema de los puentes de Königsberg», un clásico de la teoría de grafos.
Su mente excepcional dejó una obra colosal, desarrollada en las academias científicas punteras del siglo XVIII, la de San Petersburgo y la de Berlín. Cuando Euler llegó a la Academia de Berlín invitado por Federico el Grande de Prusia, en 1741, ya hacía diez años que se había quedado tuerto. Fueron los problemas con su visión los que hacen de Euler un caso único entre los de su ramo: fue ciego de un ojo durante más de 36 años y de ambos durante los siguientes 22 años. El citado monarca Federico el Grande lo apodó el cíclope matemático. Sin embargo, esto no fue obstáculo para que Euler realizara publicaciones de élite, según estimaciones de sus biógrafos, a un ritmo de unas 800 páginas por año. Su capacidad para memorizar y calcular números fue insólita.
Euler falleció un 18 de septiembre de 1783 a la edad de 76 años en la ciudad rusa de San Petersburgo (por entonces perteneciente al Imperio Ruso) tras sufrir un accidente cerebrovascular. En su honor, la imagen de Euler ha aparecido en una serie de los billetes de diez francos suizos, en sellos postales de Suiza y de Alemania e incluso hay un asteroide que lleva su nombre.
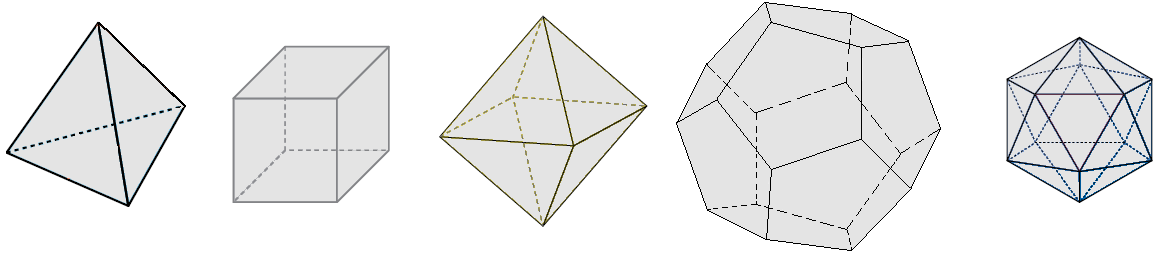
Una de sus contribuciones más espectaculares fue la famosa Fórmula de Euler para poliedros. El resultado es el siguiente: » En todo poliedro convexo con un número C de caras, un número A de aristas y un número V de vértices se cumple que: C + V − A = 2 «.
Poliedro convexo es aquel en el que dados dos puntos cualesquiera que se encuentran dentro del poliedro, el segmento que los une se encuentra también dentro del mismo.
La cantidad de figuras que cumplen la definición de poliedro convexo es tan enormemente grande que parece increíble que todos cumplan la misma fórmula. Este hecho hace que se califique a la fórmula de Euler como una maravilla matemática.