Lineal frente a no lineal
En los primeros cursos de secundaria, cuando a un alumno se le plantea la cuestión sobre cómo averiguar si dos magnitudes son directamente proporcionales, suelen ser habituales respuestas de este estilo:
«Si al aumentar una, también aumenta la otra, entonces son directamente proporcionales»
La justificación es incorrecta. Pensemos por ejemplo en la siguiente situación: en los primeros años de vida, a medida que aumenta el tiempo, también aumenta la estatura de una persona. ¿Significa eso que tiempo de vida y estatura de una persona son magnitudes directamente proporcionales? Recordemos qué es lo correcto: si al multiplicar un valor cualquiera de la magnitud X por un número, el correspondiente valor de la magnitud Y queda multiplicado por ese mismo número, entonces X e Y son directamente proporcionales.
| X | a | 2a | 3a | 4a | 5a | … |
| Y | b | 2b | 3b | 4b | 5b | … |
Según esto, si el tiempo de vida y la estatura de una persona fueran directamente proporcionales, un niño que a los 4 años alcance 1 m de estatura, conforme pase el tiempo debería alcanzar … ¡ 2 m a los 8 años ! … y … ¡ 3 m a los 12 años !
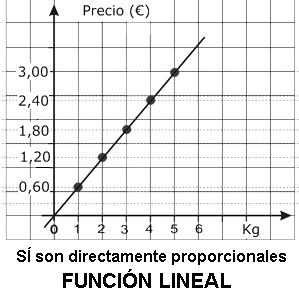
La representación gráfica asociada a una función en la que las variables son directamente proporcionales, es siempre una inconfundible línea recta. De ahí que a este tipo de funciones se les llame lineales. Por ejemplo, la función que relaciona la cantidad comprada de un producto en kg con el coste en euros, es lineal ya que ambas variables son directamente proporcionales.
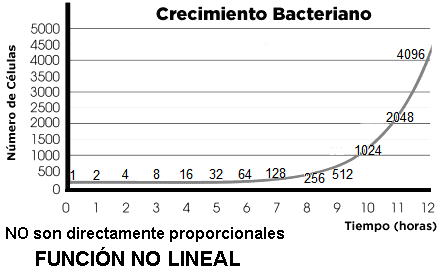
En cambio, durante la reproducción de una bacteria por bipartición, la función que relaciona el tiempo transcurrido con el número de bacterias no es lineal, ya que las variables no son directamente proporcionales, aunque cumpla aquello de que «a más tiempo, más bacterias».
a) Encuentra otra pareja de magnitudes que cumplan el argumento: «Al aumentar una, también aumenta la otra» pero que no sean directamente proporcionales.
b) Escribe la expresión analítica de la función que relaciona matemáticamente las variables Peso (kg) y Precio (€) en la primera gráfica.
c) Escribe la expresión analítica de la función que relaciona matemáticamente las variables Tiempo (horas) y Número de células en la segunda gráfica.