La fórmula de Báskara
¿Desde cuándo las ecuaciones del tipo ax2+bx+c = 0 se resuelven con la famosa fórmula que actualmente se enseña en las escuelas? ¿A quién debemos dicha fórmula?
Actualmente hay evidencias de que en Babilonia hacia el año 1600 a.C. ya se conocía un método para resolver ecuaciones de segundo grado. El trabajo de los babilonios tiene un notable valor, teniendo en cuenta que no disponían aún de la moderna notación algebraica.
Más tarde, matemáticos griegos y árabes consiguieron resolver ecuaciones de segundo grado valiéndose de representaciones geométricas, como se refleja en el libro II de los Elementos de Euclides. En la antigua Grecia destacó especialmente Diofanto de Alejandría (200 – 284), del que se tienen muy pocos datos biográficos.
También es escasa la información biográfica que se conserva del matemático persa y de lengua árabe Al-Khwarizmi (780 – 850). La palabra álgebra, con la que hoy se conoce a una de las ramas de las matemáticas, aparece en el título de su obra más importante. En dicha obra resuelve seis tipos de ecuaciones de segundo grado con una incógnita. A lo largo de los seis capítulos aparecen catorce ecuaciones, junto con las estrategias que se deben aplicar en cada caso para resolverlas.
Por cierto, el empleo de la letra x para representar a una incógnita se debe al matemático persa Omar Khayyam (1048 – 1131). En sus escritos, para referirse a un dato desconocido, utiliza el término árabe shay, que significa «la cosa». Esta palabra fue traducida al castellano antiguo como xay en las obras científicas de la época, término que fue reemplazado progresivamente por su inicial, la letra x, convirtiéndose en símbolo universal de la incógnita.
La fórmula que permite determinar las soluciones de la ecuación no se obtuvo hasta el siglo XII. Se la debemos al matemático indio Bháskara Acharia (1114 – 1185), conocido en español como Báskara. Su demostración puede resumirse así:
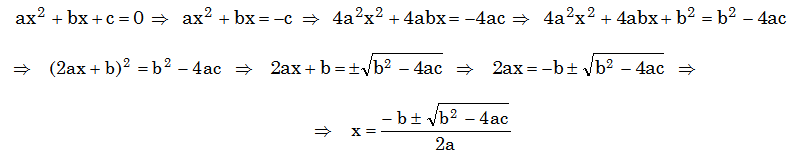
También existen fórmulas para resolver ecuaciones de tercer y cuarto grado, pero son más largas y bastante más complicadas de deducir. Para ecuaciones de quinto grado o más ni existen fórmulas ni existirán. Este resultado fue demostrado en 1824 por el matemático noruego Niels Enrik Abel (1802 – 1829).