El número áureo

«El Diablo de los Números» es un libro para adolescentes escrito en 1997 por el poeta y ensayista alemán Hans Magnus Enzensberger. Sus protagonistas son un niño llamado Robert y el «diablo de los números», que enseña a Robert, con un vocabulario un tanto peculiar, esas matemáticas que odia porque no las consigue entender en el colegio.

Su tratamiento de términos y conceptos matemáticos han hecho de «El Diablo de los Números» un libro recomendable para comprender nociones básicas de las matemáticas de forma amena.

La siguiente lectura es un extracto adaptado de uno de sus capítulos dedicado al número áureo:

« − Toma, te he traído una cosa.

Esta vez no era una simple calculadora de bolsillo. La cosa era gris plata, con una pequeña pantalla que se podía abrir.

− ¡Un ordenador! −exclamó Robert.

− Sí −dijo el anciano−. Una especie de portátil. Si quieres podemos empezar. ¿Por qué no tecleas unos cuantos números de Fibonacci?

Robert tecleó, y en la pantalla apareció la serie: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 …

− Ahora prueba a dividirlos −dijo el viejo maestro−. Siempre por parejas sucesivas. El mayor dividido entre el menor.

− Bien −respondió Robert. Tecleó y tecleó, curioso por saber lo que leería en la pantalla:

1: 1 = 1                  2 : 1 = 2                  3 : 2 = 1,5                  5 : 3 = 1,666…                  8 : 5 = 1,6       

13 : 8 = 1,625                                    21 : 13 = 1,615384615…              34 : 21 = 1,619047619… 

55 : 34 = 1,61764705882…             89 : 55 = 1,618181818…             144 : 89 = 1,61797752808…  

− ¡Es una locura! −dijo Robert−. Otra vez esos números que nunca cesan. El 18 que se muerde la cola. Y algunos de los otros tienen un aspecto completamente irracional.

− Sí, pero aún hay otra cosa −le hizo notar el anciano. Robert reflexionó y dijo:

− Todos esos números varían arriba y abajo. El segundo es mayor que el primero, el tercero menor que el segundo, el cuarto otra vez un poquito mayor, y así sucesivamente. Siempre arriba y abajo. Pero, cuanto más dura esto, menos se alteran.

− Exactamente. Cuando coges números de Fibonacci cada vez más grandes, los cocientes se acercan, oscilando, cada vez más hacia el número 1,618… Pero no creas que éste es el final de la historia, porque lo que sale es un número irracional que nunca se termina. Te aproximas a él cada vez más, pero por más que calcules, nunca lo alcanzarás del todo.

− Está bien −dijo Robert−. Los números de Fibonacci son así. Pero, ¿por qué oscilan así en torno a ese número en particular?

− Eso −afirmó el anciano− no tiene nada de particular. Es lo que hacen todos.

− ¿Qué quieres decir con todos?

− No tienen por qué ser los números de Fibonacci. Dime los dos primeros que se te ocurran.

− Diecisiete y once −dijo Robert.

− Bien. Ahora por favor súmalos. Y después haz lo mismo con los dos últimos números que vayas obteniendo.

− Puedo hacerlo de cabeza: 28, ……y el siguiente es 17 + 28, o sea, 45.

− Magnífico. Te enseñaré en la pantalla cómo sigue: 11, 17, 28, 45, 73, 118, 191, 309, 500 …

− Comprendido −dijo Robert−. ¿Y ahora qué?

− Haremos lo mismo que hemos hecho con los números de Fibonacci. Dividir. Prueba tranquilamente a hacerlo.

En la pantalla aparecieron las cifras que Robert tecleaba, y lo que resultó fue esto:

17: 11 =  1,545454…                                             28 : 17 =  1,6470588235294…       

45 : 28 =  1,607142857142857142…                 73 : 45 = 1,62222…     

118 : 73 =  1,61643835616438…                       191 : 118 =   1,61864406779661…

309 : 191 = 1,6178010471204…                         500 : 309 = 1,6181229773…

− Exactamente el misma número absurdo 1,618…−exclamó Robert−. No lo entiendo. ¿Es que está dentro de todos los números? ¿Funciona esto de verdad siempre? ¿Empezando por dos números cualquiera? ¿Sin importar cuáles elija?

− Sin duda −dijo el viejo maestro−. »

Aclaración

El número 1,61803398… protagonista del texto que has leído, es un número irracional conocido con el nombre de Número Áureo  o  Número de Oro.

También es conocido como razón áurea ya que, por definición, es la razón entre dos medidas distintas que cumplen la siguiente propiedad:

«La mayor es a la menor como la suma de ambas es a la mayor»

En otras palabras, si se representan estas medidas con las letras  a  y  b, siendo a > b, la razón áurea es el número  «a dividido entre b», donde  a  y  b  cumplen la proporción

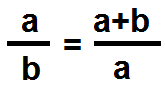 que se lee así:  «el segmento  a  es al segmento  b  como el segmento  a+b  es al segmento  a»

Con el siguiente procedimiento algebraico, se obtiene el valor exacto del Número Áureo: