El truco de Gauss
 «Malditas matemáticas. Alicia en el País de los Números» es un libro para adolescentes escrito en 2000 por el guionista de televisión y matemático italo-español Carlo Frabetti. La protagonista es una niña llamada Alicia, a la que se le aparece por sorpresa el matemático Lewis Carroll (autor de Alicia en el País de las Maravillas), para guiarla hasta el «País de los Números«, donde descubrirá los secretos que guardan esas matemáticas que tanto le aburren.
«Malditas matemáticas. Alicia en el País de los Números» es un libro para adolescentes escrito en 2000 por el guionista de televisión y matemático italo-español Carlo Frabetti. La protagonista es una niña llamada Alicia, a la que se le aparece por sorpresa el matemático Lewis Carroll (autor de Alicia en el País de las Maravillas), para guiarla hasta el «País de los Números«, donde descubrirá los secretos que guardan esas matemáticas que tanto le aburren.
«Malditas matemáticas» es interesante y divertido, de lectura sencilla, que ayuda a comprender nociones básicas de las matemáticas en compañía de los personajes creados por Lewis Carroll.
La siguiente lectura es un extracto adaptado de uno de sus capítulos dedicado a la suma de los términos de una progresión aritmética:
« — ¿Conoces otros trucos para contar deprisa y sin esfuerzo?
— Desde luego. Te voy a contar uno muy bueno que descubrió un niño de tu edad. Se llamaba Carl Friedrich Gauss, y llegó a ser uno de los matemáticos más grandes de todos los tiempos. Un día un profesor mandó a toda la clase como castigo, sumar todos los números del 1 al 100… El caso es que el pequeño Gauss efectuó la suma en apenas unos segundos.
— ¿Cómo pudo hacerlo?
— Pues muy sencillo. Se dio cuenta de que podía emparejar así los cien primeros números:
1 + 100 = 101 2 + 99 = 101 3 + 98 = 101 …. 48 + 53 = 101 49 + 52 = 101 50 + 51 = 101
— De este modo, se obtiene cincuenta veces 101, por lo que la suma total es 50 x 101 = 5 050.
— Muy astuto, el pequeño Gauss.
— Sin proponérselo, había descubierto la fórmula que expresa la suma de los términos de una progresión aritmética.
— Ya estás hablando otra vez como un profe —se quejó Alicia.
— Tranquila, que enseguida te lo explico. Una progresión aritmética es, sencillamente, una serie de números en la que cada uno es igual al anterior más una cantidad fija, que se llama diferencia. La progresión aritmética más sencilla es, precisamente, la sucesión de los números naturales: 1, 2, 3, 4, 5…, porque cada número es igual al anterior más 1. Por otro lado, la sucesión de los números impares: 1, 3, 5, 7, 9…
— Es una progresión aritmética de diferencia 2; y la de los pares también —concluyó Alicia.
— Exacto. Como muy bien has dicho, la sucesión 2, 4, 6, 8, 10… también es una progresión aritmética. Vamos a calcular la suma de sus diez primeros términos.
— ¿Usando el truco del pequeño Gauss?
— Sí, pero vamos a hacerlo de una forma ligeramente distinta para verlo más claro. Primero escribo esos diez primeros términos en su orden normal y luego, debajo, en orden inverso…
| 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 |
| 20 | 18 | 16 | 14 | 12 | 10 | 8 | 6 | 4 | 2 |
— ¿Para qué los escribes dos veces?
— Ahora sumamos las dos series, y vemos que diez veces 22 (que es 20+2, o sea, el primer término más el último) es el doble de la suma de los diez términos, ya que los hemos contado todos dos veces.
| 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 |
| +20 | +18 | +16 | +14 | +12 | +10 | +8 | +6 | +4 | +2 |
| 22 | 22 | 22 | 22 | 22 | 22 | 22 | 22 | 22 | 22 |
Por lo tanto, la suma que buscamos será (22 por 10) dividido entre 2, que es igual a 110.
— Y esto se puede hacer con todas las progresiones aritméticas —comentó Alicia.
— Claro. Si llamamos p al primer término, u al último, n al número de términos y S a la suma total, la fórmula general válida para todos los casos es

En el caso de los cien primeros números naturales, p = 1, u = 100 y n = 100. Por lo tanto,
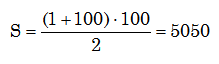
como ya sabíamos. »
