Lectura U.D. 05 – Ecuaciones de Lotka-Volterra: modelo presa-depredador
Resulta intuitivo pensar que las poblaciones de un animal depredador y su presa están relacionadas de algún modo en el que si una aumenta, la otra lo hace también. Utilizaremos como ejemplo en este artículo un ecosistema aislado y formado por leones y cebras que viven en armonía, es decir, los leones comiéndose a las cebras. Imaginemos que por cualquier circunstancia, por ejemplo, por disponer de mayor cantidad de alimento, aumenta la población de cebras; los leones dispondrán de más alimento y su población aumentará, pero ¿qué ocurrirá a partir de este momento? Si la población de leones llega a ser demasiado grande para el número de cebras en nuestra sabana, podrían acabar con todas, provocando su propia extinción por inanición. Pero incluso si el festín no es tan grande como para comerse todas las cebras, pero sí para dejar una población muy mermada, probablemente los leones tendrán que pasar hambre una buena temporada y algunos de ellos morirán hasta que las cebras tengan tiempo suficiente para reproducirse y volver a ser pasto de los leones. ¿Cuántas cebras morirán en el atracón? ¿Cuánto tiempo pasarán los leones hambre? ¿Cuántos morirán?
Este comportamiento, predador y presa conviviendo en un medio cerrado, fue estudiado por dos matemáticos que encontraron un sencillo sistema de ecuaciones que explica cómo evolucionan esas poblaciones: las ecuaciones de Lotka-Volterra. Sirven para explicar muchísimos otros ejemplos del tipo predador-presa como zorros-liebres, orugas- pinos,tiburones-calamares, siempre que las condiciones sean más o menos de aislamiento,
es decir sin la interferencia de otros predadores o migraciones.
Hipótesis
Las ecuaciones de Lotka-Volterra son un modelo biomatemático que pretende responder a estas cuestiones prediciendo la dinámica de las poblaciones de presa y depredador bajo una serie de hipótesis:
- El ecosistema está aislado: no hay migración, no hay otras especies presentes, no hay plagas…
- La población de presas en ausencia de depredadores crece de manera exponencial: la velocidad de reproducción es proporcional al número de individuos. Las presas sólo mueren cuando son cazadas por el depredador.
- La población de depredadores en ausencia de presas decrece de manera exponencial.
- La población de depredadores afecta a la de presas haciéndola decrecer de forma proporcional al número de presas y depredadores (esto es como decir de forma proporcional al número de posibles encuentros entre presa y depredador).
- La población de presas afecta a la de depredadores también de manera proporcional al número de encuentros, pero con distinta constante de proporcionalidad (dependerá de cuanto sacien su hambre los depredadores al encontrar una presa).
Resolución de las ecuaciones: La naturaleza es sabia
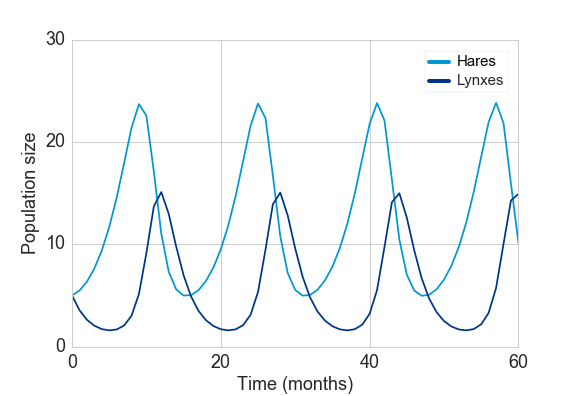
Obtenemos un modelo cíclico que se repite en el tiempo:
– Cuando el número de presas aumenta porque hay menos depredadores, con unos meses de retardo empieza a crecer el número de depredadores pues pueden comer, hasta que llega un momento que las presas empiezan a decrecer.
– Cuando se cruzan las dos gráficas la primera vez las presas ya están decreciendo intensamente y a continuación lo hacen también los depredadores: no tienen comida.
Hay un momento que las presas se recuperan pues hay pocos depredadores, incluso aumentan muy rápido lo que hace que con cierto retardo empiecen a crecer los depredadores también y se repite el ciclo.
Lo más sorprendente es que su aplicación se sale del campode la naturaleza y entra de lleno en el comportamiento humano: situaciones de guerra entre dos países; epidemias; productos económicos; policías y ladrones; etc.
Fuentes: Álex Saez