Lectura U.D. 10 – Clotoide, la curva que vela por tu seguridad
Clotoide, la curva que vela por tu seguridad en carreteras y ferrocarriles
Los primeros trazados de carreteras y vías férreas encadenaban tramos rectos con arcos de circunferencia. Pero, cuando coches y trenes alcanzaron velocidades más altas, se producía una incómoda y peligrosa sacudida al entrar en la curva. Los ingenieros comenzaron a buscar una solución, y la encontraron en las matemáticas y la física. ¿Quieres una explicación sencilla de por qué se usa la clotoide como curva de transición?
Imagina que tienes que diseñar una autovía o una vía férrea de alta velocidad. Seguro que intentarás que haya todas las rectas posibles, pero también tendrás que hacer alguna curva. Y como la más sencilla de todas es la circunferencia, lo más fácil sería ir empalmando tramos rectos con arcos de circunferencia. Algo parecido a una cinta transportadora.
Parece que así fueron los primeros trazados y, como los primeros coches y trenes no iban a mucha velocidad, todo iba como la seda. Pero la cosa cambió cuando los vehículos fueron capaces de alcanzar velocidades mayores. Al entrar en la curva, en las uniones entre tramos, se notaba una súbita sacudida. Mal asunto.
Así que los ingenieros comenzaron a estudiar qué pasaba y cómo se podía solucionar. La respuesta es fácil de entender y sólo necesitarás dos ingredientes.
El primero viene de la geometría y es el radio de curvatura, un concepto bastante intuitivo. Para una circunferencia, el radio de curvatura es simplemente el radio de la circunferencia. Para una recta puedes pensar que ésta es una circunferencia muy grande, de radio infinito. Así el radio de curvatura de una recta será infinito. ¿Fácil, verdad?
[…]
El segundo ingrediente viene de la física y es la fuerza centrífuga. A menor radio y mayor velocidad más grande es esta fuerza que nos quiere “explusar” de la curva
En los puntos de unión de rectas con arcos, el radio de curvatura (r) pasaba de ser infinito (si lo prefieres, un número muy grande) a ser un número más o menos pequeño (el radio (R) de la circunferencia). Es cecir tenemos que girar el volante para adecuar el giro a la curva de forma instantánea, y por eso se producía un aumento brusco de la fuerza centrífuga y la citada sacudida
La solución a esta incómoda y peligrosa situación fue introducir una curva de transición entre la recta y la circunferencia. Además sería genial que, en esa transición, el radio de curvatura (r) fuera disminuyendo suavemente desde el infinito (o número muy grande) de la recta hasta el radio (R) de la circunferencia. De esta forma tenemos cierto margen para ir adecuando el giro de volante a la curva de forma progresiva lo que redunda en que la fuerza centrífuga también cambiara de manera suave en vez de brusca.
[…]
Justo esta propiedad es la que define a la curva clotoide, que ya conocían matemáticos y físicos. Se trata de una espiral cuya ecuación es precisamente
ρ·s=C2 , siendo
ρ el radio de la curva
s la longitud del arco de curva
C la constante de espiral
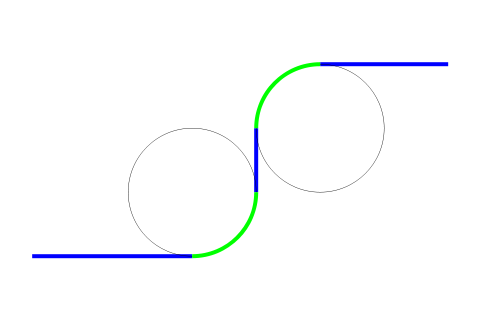
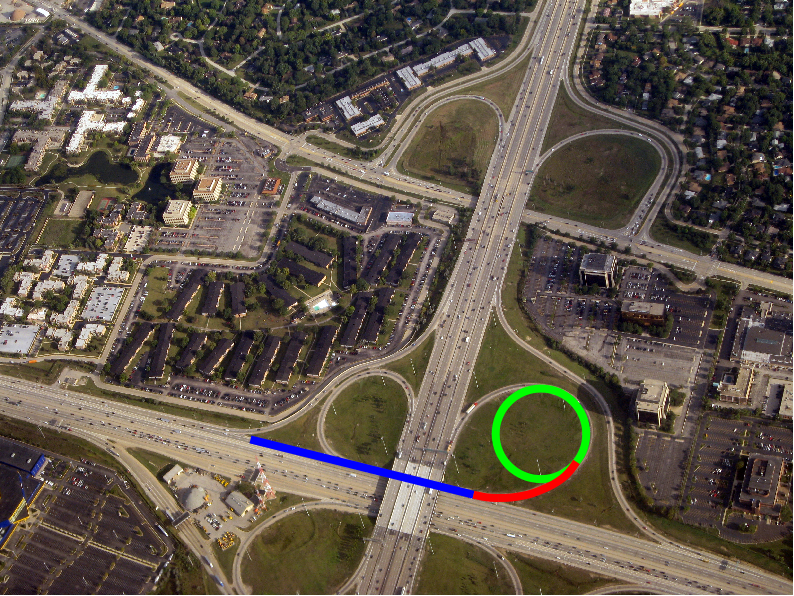
Por eso en tus carreteras y ferrocarriles las curvas suelen encadenar tramos de recta – clotoide – circunferencia – clotoide – recta. De ese modo la fuerza centrífuga va cambiando gradualmente y puedes girar el volante de forma progresiva, en vez de tener que hacerlo bruscamente.
La próxima vez que tomes una curva, no olvides que las matemáticas y la física estarán allí para ayudarte
Texto original de David Orden, publicado en https://cifrasyteclas.com/clotoide-la-curva-que-vela-por-tu-seguridad-en-carreteras-y-ferrocarriles/