Puedes utilizar este formulario para practicar tus conocimientos en formulación.
[WpProQuiz 5]
Practica la formulación (1º Bach)
[WpProQuiz 5]
[WpProQuiz 5]
Campo gravitatorio terrestre
¿Cuándo podemos considerar un comportamiento uniforme del campo gravitatorio terrestre ?
Sabemos que las líneas del campo gravitatorio son radiales y que el valor de la intensidad del campo gravitatorio va disminuyendo a medida que nos alejamos de la masa que genera el campo, por tanto la respuesta a la pregunta es nunca.
Pero, podemos aproximarnos bastante tomando un pequeño volumen (en comparación con el radio terrestre) en las proximidades de la superficie terrestre. Unos cálculos bastantes sencillos nos llevan a un volumen que corresponde a un paralelepípedo rectangular de unos 110 km de largo por 110 km de ancho y unos 30 km de altura (Se ha considerado que el valor de la intensidad del campo gravitatorio es inferior al 1% y se considera plano si el ángulo es inferior a 1º) . En este volumen, podemos considerar el comportamiento del campo gravitatorio como uniforme, y esto implica que en todos los puntos de este volumen la intensidad del campo gravitatorio es la misma, y en consecuencia las líneas de campo se pueden considerar paralelas.
En la figura se hace una representación de la intensidad del campo gravitatorio y de las superficies equipotenciales para «este campo gravitatorio terrestre».
Potencial gravitatorio
Además de caracterizar el campo gravitatorio por la intensidad del campo gravitatorio (fuerza por unidad de masa), que es una magnitud vectorial, se puede asignar a cada punto del campo una magnitud escalar, el potencial gravitatorio ,U, que se define como la energía potencial gravitatoria por unidad de masa colocada en ese punto.
Si tenemos en cuenta el valor de la energía potencial gravitatoria en el punto A:
(I)
entre dos puntos A y B, la expresión queda:
Definido de esta forma, el valor del potencial gravitatorio en el infinito es cero.
U(A)- U(B) recibe el nombre de diferencia de potencial entre eso dos puntos, y representa el trabajo por unidad de masa que realiza el campo para trasladar la unidad de masa desde el punto A hasta el B.
Por su definición, el potencial gravitatorio es una magnitud escalar, cuyas dimensiones son energía/masa, y en el Sistema Internacional se mide en J/kg. De acuerdo con la expresión (I), el potencial gravitatorio tiene el mismo valor en todos los puntos que estén a la misma distancia de la masa que origina el campo. En el espacio que rodea a la masa que genera el campo, las superficies equipotenciales son esféricas (en el plano son circunferencias ) concéntricas y de valores creciente para radios cada vez mayores. Dada la forma de las superficies equipotenciales, resulta evidente que el vector intensidad del campo gravitatorio es perpendicular en todos los puntos a la superficie equipotencial. El sentido de la intensidad del campo gravitatorio es el de los potenciales decrecientes.
Practica la formulación.
Puedes utilizar este formulario para practicar tus conocimientos en formulación.
[WpProQuiz 2]
Problema-2 Cinemática
Un gran peñasco descansa sobre un barranco, 400 metros por encima de un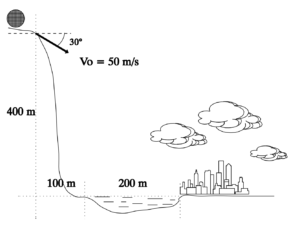 
pueblo, en tal posición que si rodase, saldría despedido con una rapidez de 50 m/s. Existe una laguna de 200 m de diámetro con su borde a 100 metros del borde del barranco, como aparece en la figura. Las casas del pueblo están junto a la laguna. Un alumno de física afirma que el peñasco caería dentro de la laguna. ¿Está en lo cierto? Dato: aceleración de la gravedad 9,8 ms-2
Interacción electromagnética: introducción y algunas experiencias.
Primer punto de los contenidos del Bloque-III de Física de 2º de Bachillerato: Interacción electromagnética.
Los primeros fenómenos magnéticos de los que se tienen noticias están relacionados con el mineral de hierro encontrado cerca de la antigua ciudad griega de Magnesia. Se había observado que los fragmentos de este mineral, que recibe el nombre de magnetita, atraían pequeños trozos de hierro.
Los chinos, en el año 121 de nuestra era, sabían que una varilla de hierro puesta cerca de un imán natural adquiría las mismas propiedades que éste y que, si se colgaba un imán de un hilo, se orientaba en la dirección norte sur.
El primer estudio sistemático de los fenómenos eléctricos y magnéticos fue realizado en la segunda mitad del siglo XVI, por el médico inglés William Gilbert. Gilbert diferenció los dos tipos de fenómenos y fue el primer científico, que consideró a la Tierra como un gran imán.
Los imanes atraen el hierro, siendo más pronunciado el efecto en determinadas zonas del imán llamadas polos.
En un imán se distinguen dos polos magnéticos, que designamos arbitrariamente como norte y sur, y que presentan la propiedad de repelerse si son de la misma polaridad y de atraerse si son de polaridad distinta.
Este hecho, unido a que la fuerza entre los polos es inversamente proporcional al cuadrado de la distancia que los separa, llevó a pensar que los fenómenos magnéticos eran análogos a los eléctricos y estaban originados por una propiedad de la materia llamada polo magnético.
Una dificultad que se aprecia en esta teoría surge al comprobar que los polos magnéticos no se encuentran nunca separados como sucede con la carga eléctrica. En el estudio del magnetismo, esta dificultad se puede salvar si describimos las acciones magnéticas utilizando el concepto físico de campo. Un imán crea, en los puntos de su alrededor, un campo magnético que se pone de manifiesto al colocar en ellos otro imán o un cuerpo de material magnético.
Una forma de hacer “visible” este campo se obtiene cuando colocamos sobre un imán una hoja de papel y esparcimos limaduras de hierro sobre ella. En estas condiciones observamos que las limaduras se distribuyen sobre esta superficie de forma que nos proporcionan una idea de la geometría de las líneas del campo magnético.
Las líneas del campo magnético son líneas cerradas. Por convenio se admite que las líneas de campo salen del polo norte y entran por el polo sur del imán.
Hasta finales de 1819 no se demostró ninguna relación entre los fenómenos eléctricos y magnéticos. La primera experiencia que puso de manifiesto la interrelación entre estos dos tipos de fenómenos fue debida al científico danés Hans Christian Oersted (1777-1851).
Oersted situó una brújula en las proximidades de un hilo conductor por el que hizo circular una corriente eléctrica continua. Observó que, cuando por el hilo pasa corriente, la aguja se orienta perpendicularmente al hilo. Por el contrario, cuando cesa el paso de la corriente, la aguja vuelve a su posición inicial. Si se invierte el sentido de la corriente, la aguja varía el sentido Norte – Sur.
El trabajo de Oersted demostró que el movimiento de las cargas eléctricas produce efectos magnéticos.
Experimentalmente se observa otra serie de fenómenos que refuerza la afirmación de que las cargas eléctricas en movimiento producen los mismos efectos que los imanes.
- Al situar dos conductores paralelos por los que circulan corrientes de intensidades grandes, aparecen fuerzas entre ambos, que son de atracción, si las corrientes llevan el mismo sentido y, de repulsión, si las corrientes llevan sentido contrario. Cuando cesa el paso de la corriente, las fuerzas dejan de actuar. La primera observación de este hecho fue realizada por Ampère, en el mismo año que realizó Oersted su experimento.
- También entre dos conductores circulares (espiras) paralelos, recorridos por sendas corrientes continuas, se producen fuerzas de atracción, si el sentido de la corriente que recorre a cada una de ellas es el mismo, y de repulsión, si estos sentidos son contrarios.
- Entre una espira por la que circula corriente continua y un imán permanente se generan también atracciones y repulsiones.
Podemos concluir: una carga eléctrica produce un campo eléctrico y, si la carga está en movimiento , produce además un campo magnético. La interrelación entre el campo eléctrico y el campo magnético da lugar al electromagnetismo.
Al igual que hicimos con las fuerzas gravitatorias y las fuerzas eléctricas, las fuerzas magnéticas también las describiremos usando el concepto de campo. Empezaremos este tema estudiando cómo las cargas eléctricas y las corrientes responden a los campos magnéticos; terminaremos estudiando cómo las cargas en movimiento producen campos magnéticos.
Redes de difracción
Se describe el funcionamiento de una red de difracción cuando la luz incide sobre ella.
Una herramienta muy útil para medir la longitud de onda de la luz es la red de difracción.
Consideremos varias rendijas paralelas de igual ancho y espaciadas regularmente. Si el número de rendijas es muy elevado tenemos una red de difracción.
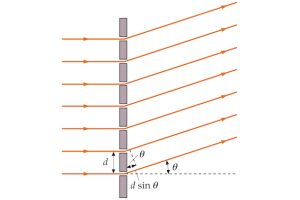
Si hacemos pasar luz a través de una red de difracción se observa un diagrama que consiste en una serie de franjas brillantes correspondientes a los máximos principales del diagrama de interferencia que están dadas por la ecuación:
siendo d la distancia entre las rendijas y n es lo que se denomina número de orden, y según el valor de n, los máximos principales se denominan primero, segundo,… orden de difracción.
Cuando sobre la red de difracción incide una luz de diversas longitudes de onda, éstas producen máximos de difracción a ángulos diferentes, excepto para el orden cero. El conjunto de máximos de un orden dado para todas las longitudes de onda constituyen un espectro. A mayor longitud de onda mayor desviación.
Física. Volumen II: Campos y Ondas; Marcelo Alonso.
Imagen: Física. Paul tipler. Ed. Reverté
Sistemas dinámicos. Teoría del Caos.
Descripción de los sistemas dinámicos.
Un sistema dinámico es un sistema que evoluciona con el tiempo. Los sistemas dinámicos se pueden clasificar en estables, inestables y caóticos.
ESTABLES
Estos sistemas se caracterizan por la existencia de leyes que gobiernan el sistema y las ecuaciones que lo rigen suelen ser lineales. Pequeños cambios en las condiciones iniciales no provocan cambios perceptibles en la situación final del sistema. Un ejemplo de un sistema estable puede ser el péndulo simple.
INESTABLES
Estos sistemas tienen una gran dependencia de las condiciones iniciales, en las que pequeñas variaciones en las condiciones iniciales provocan grandes cambios en la situación final. No hay leyes que las gobiernen. Un ejemplo de un sistema inestable puede ser un atasco de tráfico.
CAÓTICOS
Estos sistemas, aún teniendo leyes que los gobiernan, son muy sensibles a pequeñas variaciones iniciales. Aunque dan la sensación de desordenados no lo son, ya que las propiedades del sistema están fijadas por leyes. Debido a la sensibilidad extrema a las condiciones iniciales hace que su conducta sea impredecible en un tiempo relativamente largo. Ejemplo de un sistema caótico es el estudio del clima o el comportamiento de un péndulo doble.
[youtube https://www.youtube.com/watch?v=d3uOKlIEIoU]
Energía potencial gravitatoria
Llegaremos a una expresión para calcular la energía potencial gravitatoria.
Para determinar la función energía potencial (Ep) del sistema formado por una partícula de masa m y la Tierra, calcularemos el trabajo que realiza el campo (la fuerza gravitatoria) al desplazar un cuerpo de masa m por una trayectoria arbitraria desde una posición A, a una distancia rA del cuerpo de masa M responsable del campo, hasta una posición final B que dista rB de M (ver figura).
Debemos tener en cuenta que tanto la dirección como el módulo de la fuerza gravitatoria varían de un punto a otro de la trayectoria. El trabajo total será la suma de todos los trabajos elementales que se realizan en desplazamientos tan pequeños como podamos considerar .Cuando el número de estos sumandos tiende al infinito, el cálculo de esa suma infinita de sumandos nos lleva al concepto de integral y el trabajo que realiza la fuerza (campo) es:
$latex W = \int \limits_{r_A}^{r_B} \vec F \cdot d \vec r $
La fuerza gravitatoria es conservativa y en consecuencia, el trabajo realizado es independiente de la trayectoria seguida; podemos escoger una trayectoria “más cómoda” para calcular el valor de la integral anterior. La trayectoria que elegiremos será A-C-B.
El trabajo que realiza el campo desde A hasta B es:
$latex {W_{A \rightarrow B }} = {W_{A \rightarrow C }}+ {W_{C \rightarrow B }} $
Sabemos que el trabajo realizado desde C a B es cero, ya que la fuerza y el desplazamiento son perpendiculares.
$latex {W_{A \rightarrow B }} = {W_{A \rightarrow C }}=\int \limits_{r_A}^{r_B} -G \frac {M \cdot m}{r^2} \vec u \cdot d \vec r $
En el tramo A-C, el vector unitario $latex \vec u $ y el vector $latex d \vec r $ forman un ángulo de 0º , por lo que su producto escalar es igual al producto de sus módulos, es decir dr:
$latex {W_{A \rightarrow B }} = {W_{A \rightarrow C }}=\int \limits_{r_A}^{r_B} -G \frac {M \cdot m}{r^2} d r $
Resolviendo la integral:
$latex {W_{A \rightarrow B }} = \int \limits_{r_A}^{r_B} -G \frac {M \cdot m}{r^2} d r =\left. G \frac {M \cdot m}r \right |_{r_A}^{r_B}=G \frac {Mm}{r_B}-G \frac {Mm}{r_A} $
Teniendo en cuenta:
$latex W_{A \rightarrow B} = Ep(A)-Ep(B) $ y $latex {W_{A \rightarrow B }} = G \frac {Mm}{r_B}-G \frac {Mm}{r_A} $
podemos decir que:
$latex Ep(A)-Ep(B)= -G \frac {Mm}{r_A}+G \frac {Mm}{r_B} $
Definida la energía potencial de esta forma solo tiene sentido hablar de la diferencia de energía potencial gravitatoria entre dos puntos ya que es imposible conocer el valor de la energía potencial gravitatoria absoluta; parece claro, que debemos elegir un origen de energía potencial gravitatoria. Dado que la acción gravitatoria de M sobre m es nula si el cuerpo de masa m se encuentra infinitamente alejado del cuerpo M, podemos elegir el origen de energía potencial en el infinito (Ep=0), y por tanto :
$latex Ep_{A}-Ep(\infty)= -G \frac {Mm}{r_A} + 0 \implies Ep(A) = – \frac {GMm}{r_A} \ \ (origen \ Ep=0\ \ en \ el \ \infty) $
El localizar el origen de energía potencial gravitatoria en el infinito implica que la energía potencial gravitatoria es siempre negativa, y por ello aumenta su valor a medida que lo hace la distancia entre sus masas.
Concepto de campo
Concepto de campo. Escalares y vectoriales
Decimos que en una zona del espacio tenemos definido un campo vectorial , $latex \vec V $ cuando para cada punto P de esa zona , la magnitud $latex \vec V $ toma un único valor que depende exclusivamente de las coordenadas del punto P (función de posición).
Si $latex \vec V $ es una fuerza hablaremos de un campo de fuerzas.
Si la magnitud es escalar (temperatura, presión,…) tendremos un campo escalar.
Los campos que no dependen del tiempo se denominan estacionarios o estáticos.
Un campo escalar se representa mediante las superficies de nivel, que son el lugar geométrico para el cual la magnitud escalar tiene un mismo valor.
Un campo vectorial se representa gráficamente por líneas de campo, que son líneas tangentes en cada punto al vector campo definidos en ellos. En el caso de un campo de fuerzas hablaremos de líneas de fuerza.
Las propiedades de las líneas de campo son:
-
-
- Su sentido de recorrido y el del vector que representa el campo coinciden en cada punto.
- Pueden ser cerradas (campos magnéticos) o abiertas (campo gravitatorio).
- Las líneas de campo no se pueden cortar.
- Parten de manantiales y convergen en los sumideros.
- Si el campo es uniforme (el mismo valor de la magnitud en todos sus puntos del campo), las líneas de campo son paralelas.
- El número de líneas de campo es indicativo de la intensidad del campo: a mayor número de líneas de campo mayor intensidad del campo.
-