
El punto Q pertenece al plano; El punto P, no; La distancia entre P y el plano es distinta de la distancia ente P y Q
Dos elementos dimensionales pueden relacionarse entre sí en un espacio dimensional mayor, por ejemplo dos puntos en una recta, en un plano o en el espacio. Las posibles relaciones entre los elementos se dan en términos de pertenencia, distancia y ángulo.
La relación más sencilla entre dos elementos iguales es la coincidencia (dos puntos pueden ser coincidentes, o dos rectas, o dos planos). Entre dos elementos diferentes puede darse también la pertenencia del menor al mayor (un punto puede pertenecer a una recta, pero no ser coincidente con ella).
Entre dos puntos no coincidentes se establece una relación de distancia, determinada por un segmento cuyos extremos son cada uno de los puntos.

Entre dos rectas paralelas no coincidentes se establece también una relación de distancia, determinada por un segmento perpendicular a ambos cuyos extremos pertenecen cada uno a una de las paralelas.

Lo mismo ocurre entre dos planos paralelos no coincidentes: su segmento distancia es perpendicular a ambos y cada uno de sus extremos pertenece a uno de los planos.

Entre un punto y una recta, o entre un punto y un plano, la distancia se mide perpendicularmente a la dirección (o direcciones) de la recta o del plano.

Entre dos elementos dotados de dirección (rectas o planos, los puntos no tienen dirección), puede además establecerse una relación angular, determinada por la diferencia de las direcciones de cada elemento.
Entre dos rectas coplanarias, el ángulo entre ambas equivale al sector circular determinado por ambas y de centro el punto común a las rectas.

Entre dos planos, el ángulo se mide perpendicularmente a ambos, y por tanto también perpendicular a su recta intersección.
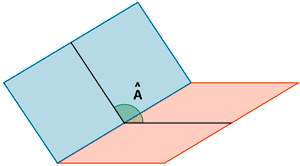
Y lo mismo entre recta y plano.
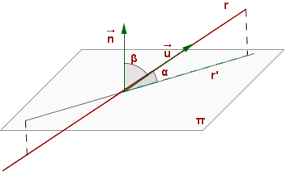
En los dos últimos casos ayuda considerar el ángulo como un sector circular perteneciente a un plano perpendicular al plano (o a los planos) y limitado por las intersecciones de este con los elementos cuyo ángulo se pretende medir.
Todo lo anterior se explica de manera gráfica en los apartados que siguen a este en esta misma web.
Comentarios recientes