En diédrico, los problemas de distancias tienen dos componentes: hallar el segmento distancia y calcular su verdadera magnitud.
El segmento distancia siempre es perpendicular al elemento o elementos que tengan dirección, y tienen como extremos puntos que pertenenen a ambos. Por ejemplo:
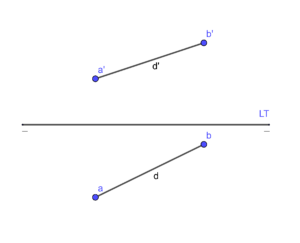
- La distancia entre dos puntos A y B es la longitud del segmento AB.

- La distancia entre un punto A y una recta r es un segmento AB perpendicular a r cuyos extremos son A y la intersección con r de la perpendicular.

- La distancia entre un punto A y un plano P es un segmento AB perpendicular a P cuyos extremos son A y la intersección con r de la perpendicular.

- La distancia entre dos rectas paralelas r y s es un segmento AB determinado por las intersecciones de r y s con un plano perpendicular a ambas.

- La distancia entre dos planos paralelos P y Q es un segmento AB determinado por las intersecciones de P y Q con una recta perpendicular a ambos.

- La distancia entre una recta r y un plano P que le sea paralelo es la de cualquier punto de r al plano.
- La mínima distancia entre dos rectas que se cruzan sin cortarse es un segmento perpendicular a ambas que las corta en sus extremos. Este problema suele resolverse mediante cambios de plano, por tratarse de un procedimiento más sencillo.




Comentarios recientes