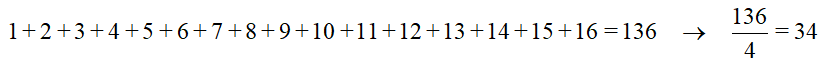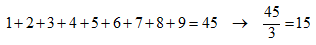En la Fachada de la Pasión de la Sagrada Familia de Barcelona, en la parte izquierda, aparece un cuadrado mágico de orden cuatro.
En este cuadrado mágico se repiten los números 10 y 14 y faltan los números 12 y 16, con lo que la constante mágica es ahora 33.
En la ciudad india de Khajuraho, en la fachada del templo Parsvanatha, hay una inscripción del año 954 d.C., con un cuadrado mágico conocido como Chautisa Yantra.
Es un cuadrado mágico construido con los dieciséis primeros números naturales, de constante mágica 34.
La suma de las cuatro filas es igual a 34.
La suma de las cuatro columnas es igual a 34.
La suma de las dos diagonales es igual a 34.
Es un cuadrado mágico pandiagonal, la suma de los números situados en las diagonales secundarias también es 34.
La suma de los cuatro números situados en las esquinas es igual a 34.
La suma de los números situados en cualquier cuadrado de 2×2 también es 34.
La suma de los números situados en las esquinas de los cuadrados de 3×3 es igual a 34.
Otros grupos de números que también suman 34.
Si se permutan cíclicamente la filas o las columnas del cuadrado mágico inicial, se obtiene otro cuadrado mágico con las mismas características.
Alberto Durero (1471-1528) es un artista renacentista alemán. Uno de sus grabados más famosos es «Melancolía I» que se encuentra en la Galería Nacional de arte de Karlsruhe (Alemania). En este grabado, realizado en 1514, hay algunos elementos matemáticos y, en la parte superior derecha, aparece un cuadrado mágico de orden cuatro.
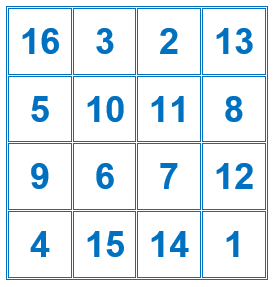
Es un cuadrado mágico construido con los dieciséis primeros números naturales, de constante mágica 34.
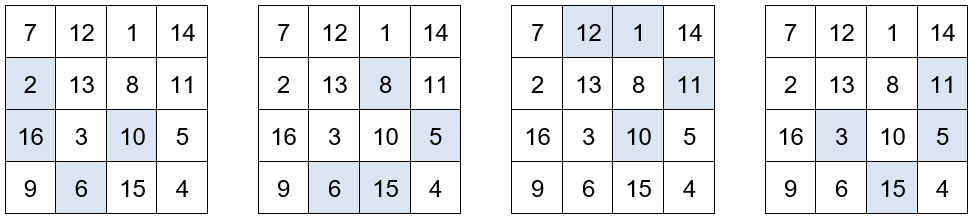
La suma de las cuatro filas es igual a 34.
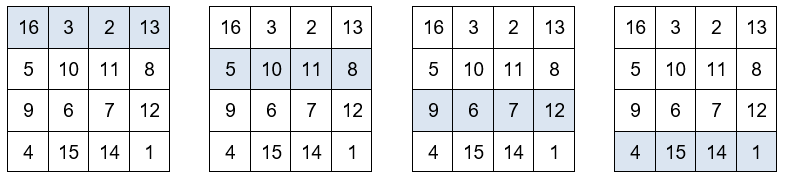
La suma de las cuatro columnas es igual a 34.
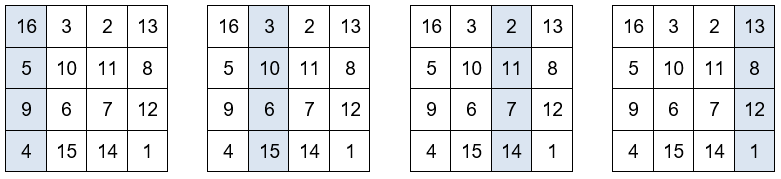
La suma de las dos diagonales es igual a 34.
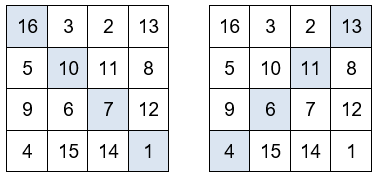
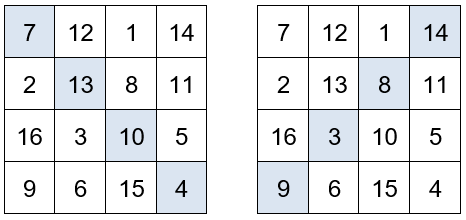
La suma de los cuatro números situados en las esquinas es igual a 34. También la suma de los números situados en los cuatro cuadrados centrales.
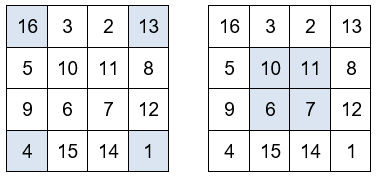
Si dividimos el cuadrado por la mitad de horizontal y verticalmente, se obtiene cuatro cuadrados con cuatro números cada uno. La suma de los números situados en cada uno de los cuadrados es igual a 34.
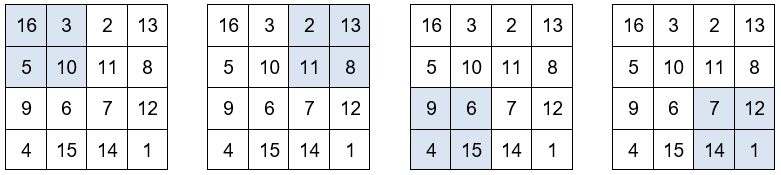
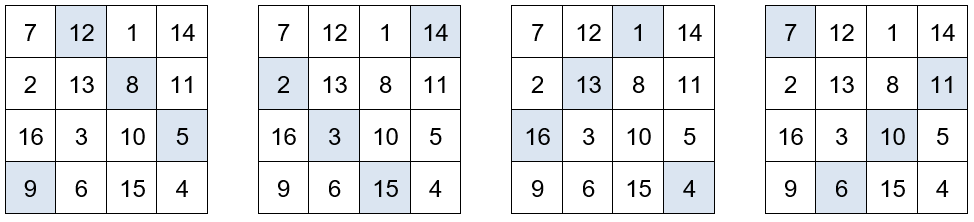
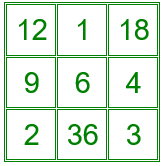
La suma los dos números centrales de la primera fila con los dos números centrales de la última es igual a 34. También la suma los dos números centrales de la primera columna con los dos números centrales de la última.
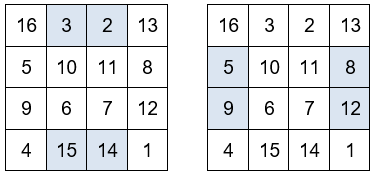
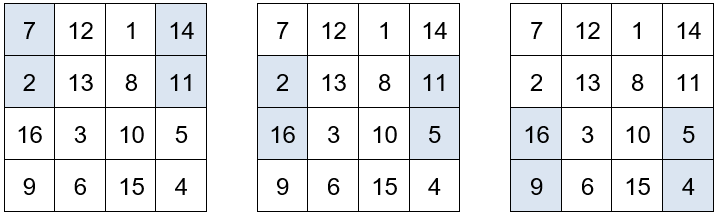
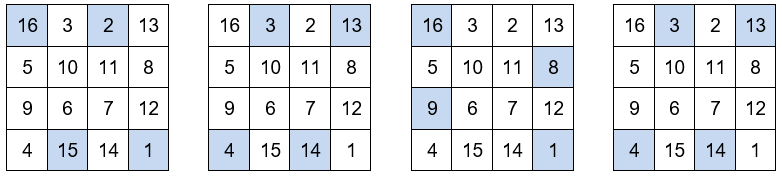
La suma de los números situados en las esquinas de los cuadrados de 3×3 es igual a 34.
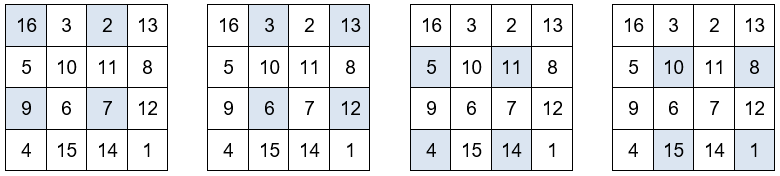
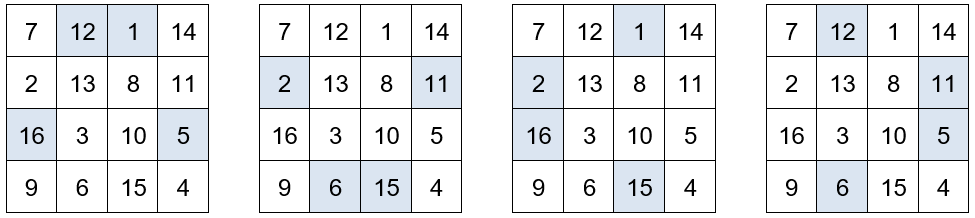
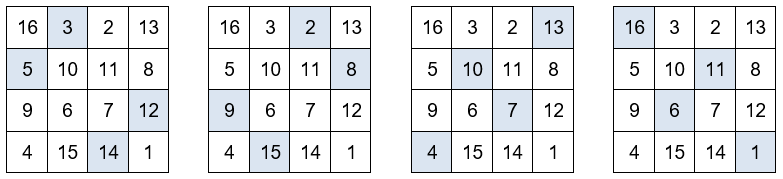
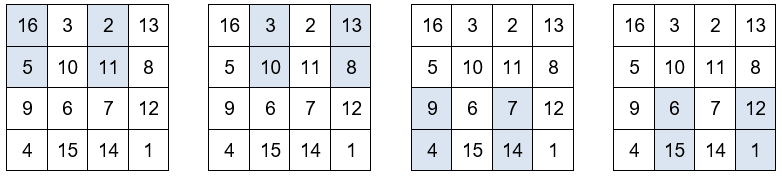
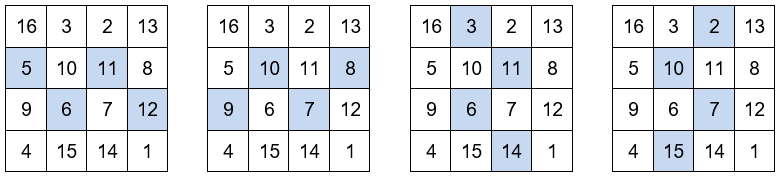
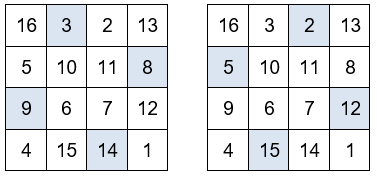
Otros grupos de números que también suman 34.
Y por último, en los dos cuadrados centrales de la última fila aparece el año de su realización, 1514. El primer número de la última fila, 4, corresponde al lugar que ocupa en el abecedario la inicial de su apellido, D. Y el último número de la última fila, 1, corresponde al lugar que ocupa en el abecedario la inicial de su nombre, A.
La constante mágica de un cuadrado de orden 4 se puede calcular sumando todos los números utilizados y dividiendo la suma por 4. Por ejemplo, la constante mágica de un cuadrado de orden 4 con los dieciséis primeros números naturales es:
La suma de las cuatro filas, las cuatro columnas y las dos diagonales principales es 34.
La constante mágica se puede calcular multiplicando todos los números utilizados y calculando la raíz de índice n del producto obtenido.
A partir del cuadrado mágico de orden 3, se pueden construir un cuadrado mágico multiplicativo con potencias de la misma base y exponente los números que aparecen en el cuadrado.
Se puede construir un cuadrado mágico multiplicativo de orden 3 con los divisores de 36.
Div(36) = { 1 , 2 , 3 , 4 , 6 , 9 , 12 , 18 , 36 }
El producto de las tres filas, las tres columnas y las dos diagonales principales es 216
La constante mágica se puede calcular sumando todos los números utilizados y dividir la suma por el orden del cuadrado mágico. Por ejemplo, la constante mágica de un cuadrado de orden 3 con los nueve primeros números naturales es:
La suma de las tres filas, las tres columnas y las dos diagonales principales es 15
