Enfriamiento de líquidos: Selección del equipo y tiempos de enfriamiento

por · Publicada · Actualizado

Tanques de enfriamiento

¡Hola a todos una semana más! El artículo de esta semana trata de arrojar un poco de luz sobre el tema de los tiempos de enfriamiento de líquidos almacenados en depósitos para diferentes procesos industriales. Hace unas semanas estudiamos cómo estimar la potencia frigorífica para enfriar líquidos, e hicimos la observación de que es muy importante verificar el tiempo de enfriamiento, ya que la potencia instalada no garantiza la velocidad de enfriamiento si otros factores no se cumplen simultáneamente. ¡Vamos a entrar en materia!

ÍNDICE

1. LA POTENCIA FRIGORÍFICA NO GARANTIZA LA VELOCIDAD DE ENFRIAMIENTO

Imaginemos la siguiente situación, hemos calculado la potencia frigorífica para enfriar el tanque de anchovetas del artículo anterior. Recordemos que se trataba de enfriar en 1 hora un tanque de 1000 L de agua desde 28 ºC iniciales hasta 7 ºC. La potencia calculada era de 24,42 kW, que se obtenía de dividir el calor total a extraer en el tanque entre el tiempo requerido. Parece sencillo, seleccionamos un equipo frigorífico que nos proporcione esta potencia, lo instalamos junto a un serpentín de enfriamiento sumergido en el tanque, y ya está resuelto, agua fría en 1 hora.

Montamos la instalación, ponemos en marcha el equipo y… el cliente nos dice que el agua no se enfría en 1 hora, que tarda casi 2 horas… Estos ingenieros… ¡Si es que ni para hacer números valéis! Nos vamos a nuestra oficina, repasamos nuestros cálculos y decimos… pero bueno, si está todo bien, ¿qué está pasando aquí? ¿Cómo puede haber tanta diferencia entre la realidad y los cálculos?

La respuesta es que hemos estado dando por hecho que nuestro equipo de 24,42 kW, va a estar proporcionando su potencia máxima durante todo el tiempo de enfriamiento, y eso es falso. A medida que el líquido se va enfriando, nuestro equipo deja de dar esos 24,42 kW, ya que el salto térmico entre el agua y el refrigerante va disminuyendo… Upsss, y ¿ahora qué hago?

Vamos a empezar a analizar por partes este problema, el cual no es sencillo. Forma parte del área de la termodinámica llamada transferencia de calor en régimen transitorio, es decir, el medio que estamos enfriando no mantiene su temperatura más o menos constante, sino que va disminuyendo. Estos fenómenos son los que ocurren cuando enfriamos por primera vez una cámara frigorífica (el aire puede pasar de 25 a 0 ºC por ejemplo) o, como en este caso, cuando enfriamos un depósito de líquido en un tiempo determinado.

 

2. SISTEMA 1: ENFRIAMIENTO DE UN LÍQUIDO CON DOS TANQUES Y UN INTERCAMBIADOR DE CALOR EXTERNO

Este es el método más simple que se le puede ocurrir al ingeniero. Tenemos un tanque a 28 ºC, tenemos otro tanque vacío, instalamos un grupo de bombeo y un intercambiador de calor entre ambos que enfríe de una sola pasada el  agua desde 28 ºC a 7 ºC, y movemos un caudal de 1000 L/h de un tanque a otro. En una hora tenemos nuestro líquido a 7 ºC en el nuevo depósito.

Este sistema nos permite tener un control total de las variables del proceso y el cálculo del sistema es muy sencillo, como veremos a continuación. El único problema es que necesitamos 2 tanques y un grupo de bombeo… El cliente seguramente nos invite a volver por donde hemos venido. Aun así, por su carácter didáctico, vamos a analizarlo, ¡que eso si es gratis!

En la Figura 1 se muestra el esquema a emplear. Para ajustar las temperaturas y los caudales de diseño, nos podemos servir por ejemplo del software de cálculo del fabricante de intercambiadores de calor SWEP o el de Danfoss (Hexact). Vamos a estudiar dos casos, en el primero utilizaremos como refrigerante agua + propilenglicol al 20%, y en el segundo caso, expansión directa con R-134a. Cabe destacar que la expansión directa está prohibida en algunos casos por la Normativa de enfriamiento de fluidos alimentarios, permitiéndose en todos los casos el enfriamiento con propilenglicol, por no ser tóxico. Seleccionaremos intercambiadores de calor de acero inoxidable a contracorriente, por ser más efectivo. Lo habitual es utilizar intercambiadores de cobre o acero para enfriar fluidos industriales no corrosivos, y el acero inoxidable para líquidos alimentarios. Si el líquido es una salmuera o agua de mar, es recomendable emplear titanio, por su alta resistencia a la corrosión.

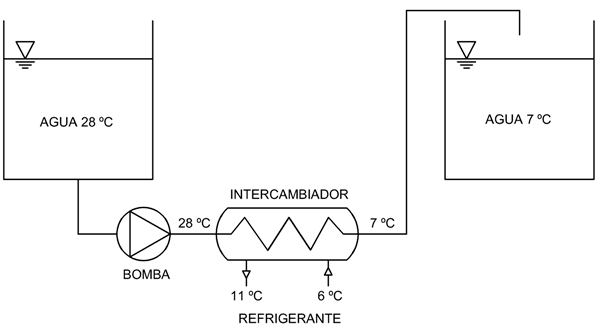
Figura 1. Esquema de enfriamiento mediante dos tanques y un intercambiador de calor externo.

Tras ajustar nuestras condiciones con el software obtenemos los siguientes resultados (más detalles en las Figuras 2 y 3):

ENFRIAMIENTO CON PROPILENGLICOL

\dot{Q}, Potencia térmica intercambiada = 24,42 kW

T_{ae}, Temperatura del agua a la entrada = 28 ºC

T_{as}, Temperatura del agua a la salida =7 ºC

T_{re}, Temperatura del refrigerante a la entrada = 6 ºC

T_{rs}, Temperatura del refrigerante a la salida = 11 ºC

\dot{m}_{a}, Caudal de agua (1000 L en 1 hora) = 0,278 kg/s

\dot{m}_{r}, Caudal de refrigerante = 1,24 kg/s

S, Superficie de intercambio = 1,30 m2

K, Coeficiente global de transmisión de calor = 3320 W/ m2 ºC

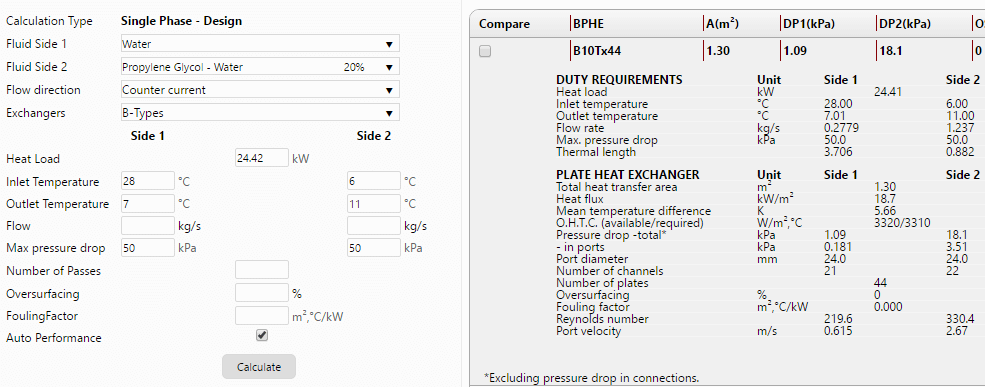
Figura 2. Datos de cálculo de intercambiador SWEP propilenglicol – agua.

ENFRIAMIENTO CON R-134a

\dot{Q}, Potencia térmica intercambiada = 24,42 kW

T_{ae}, Temperatura del agua a la entrada = 28 ºC

T_{as}, Temperatura del agua a la salida = 7 ºC

T_{r}, Temperatura de evaporación del refrigerante = 6 ºC (con 5 K de recalentamiento, Tª condensación 45 ºC y subenfriamiento 5 K)

\dot{m}_{a}, Caudal de agua (1000 L en 1 hora) = 0,278 kg/s

\dot{m}_{r}, Caudal de refrigerante = 0,163 kg/s

S, Superficie de intercambio = 3,74 m2

K, Coeficiente global de transmisión de calor = 1304 W/m2 ºC

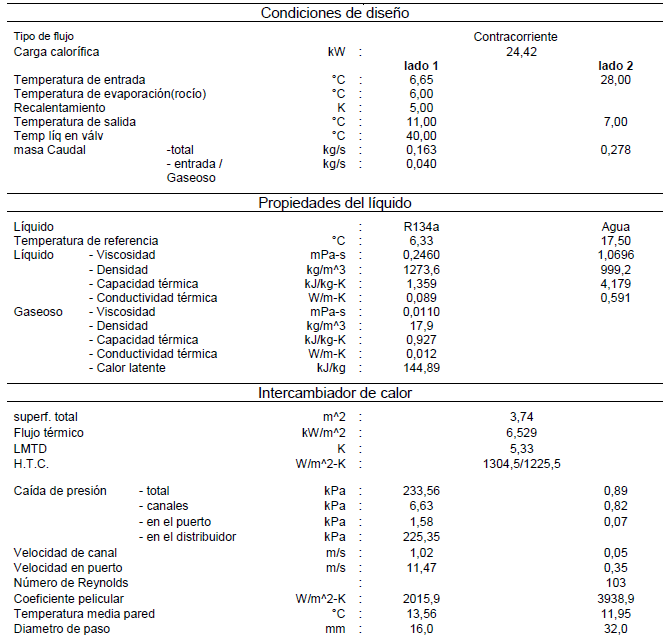
Figura 3

Figura 3. Datos de cálculo de intercambiador Danfoss R-134a – agua.

Por supuesto, sería más interesante la expansión directa, ya que obtenemos un mejor rendimiento energético de la instalación, al evitar el salto térmico necesario para enfriar el glicol hasta 6 ºC. No obstante, como hemos comentado, sería necesario consultar la Normativa si el fluido a enfriar es de carácter alimentario.

3. SISTEMA 2: ENFRIAMIENTO DE UN LÍQUIDO CON SERPENTÍN SUMERGIDO EN TANQUE

Este sistema es aparentemente el más económico en cuanto a instalación, ya que solo requiere de un serpentín sumergido en el tanque (Figura 4). No obstante, tenemos el inconveniente de que el espacio para el serpentín dentro del depósito es limitado, y a esto se suma el bajo coeficiente de transmisión de calor de este sistema, lo que es un inconveniente importante. Vamos a analizar este método para el problema que nos ocupa.

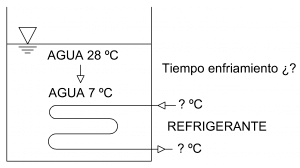
Figura 4

Figura 4. Esquema de enfriamiento mediante serpentín sumergido en tanque.

En el Sistema 1 con dos tanques que vimos anteriormente, el cálculo es muy sencillo, pero si sumergimos un serpentín frío dentro de un tanque, ¿cómo sabemos cuánto tiempo tarda el agua en enfriarse? La potencia de partida es 24,42 kW, pero con esa potencia ¿podré enfriar el tanque en 1 hora? Vamos a verlo.

El tiempo de enfriamiento de un volumen de líquido almacenado se puede obtener de manera aproximada mediante la Ley de enfriamiento de Newton:

(1)\begin{equation*} t=-\frac{\rho \cdot c \cdot V}{K \cdot S} \cdot \ln \left(\frac{T_{af}-T_{re} }{ T_{a0}-T_{r e}}\right)$ \end{equation*}

Siendo:

t, el tiempo de enfriamiento, en segundos

\rho, la densidad del agua = 1000 kg/m3

c, el calor específico del agua = 4186 J/kg ºC

V, el volumen de agua = 1 m3

K, el coeficiente global de transmisión de calor del serpentín = 100 W/m2K (sin agitador en tanque), 200 W/m2K (con agitador en tanque). Estos valores son conservadores, pueden conseguirse valores mayores generalmente.

S, la superficie de intercambio del serpentín = 8 m2 (calculados considerando que podemos meter en el tanque hasta 200 m de serpentín de acero inox de ½”).

T_{a0}, la temperatura inicial del agua = 28 ºC

T_{af}, la temperatura final del agua = 7 ºC

T_{re}, la temperatura de entrada del refrigerante = ¿? Esta es la gran incógnita

Vemos que tenemos una ecuación en la que desconocemos la temperatura del refrigerante que tendremos que emplear. Fijando el resto de variables, para cada temperatura de refrigerante tendremos un tiempo de enfriamiento distinto. Concretamente, si fijamos el tiempo en 1 hora y consideramos que no hay agitador en tanque, la temperatura del refrigerante a emplear debe ser de unos -14 ºC, es decir, 20 ºC menos de la que necesitábamos en el Sistema 1 con recirculador e intercambiador de calor. Esto es debido al bajo coeficiente K del serpentín. Si usamos agitador en el tanque, la temperatura del refrigerante a emplear es de aproximadamente 0 ºC, bastante mejor, lo que hace imprescindible usar un agitador. Por ello, continuaremos el ejemplo considerando que hay agitador (K = 200 W/m2K).

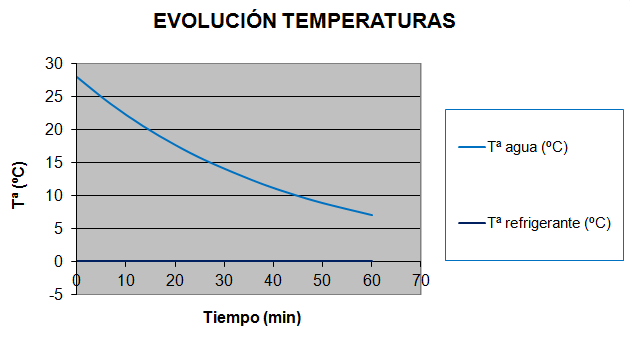
Figura 5

Figura 5. Evolución de temperatura del agua y del refrigerante durante el proceso de enfriamiento.

En la Figura 5 podemos ver la gráfica de evolución de la temperatura del tanque en función del tiempo. Vemos que inicialmente el salto térmico entre el agua y el refrigerante es 28 K, y este salto va reduciéndose hasta 7 K al final del proceso de enfriamiento. Podemos saber la potencia frigorífica que debe proporcionar el serpentín en cada fase del proceso mediante la siguiente fórmula:

(2)\begin{equation*} \dot{Q}=K \cdot S \cdot (T_a-T_{re})$ \end{equation*}

Siendo:

\dot{Q}, la potencia frigorífica, W

K, el coeficiente global de transmisión de calor del serpentín = 200 W/m2K

T_a, la temperatura del agua, en ºC

T_{re}, la temperatura de entrada del refrigerante, en ºC

Del cálculo resulta que la potencia del serpentín al comienzo del proceso debe ser de 44,80 kW, mientras que al final, debe ser de 11,20 kW, siendo la potencia media igual a 24,42 kW, justamente la que habíamos calculado inicialmente. Esto puede observarse gráficamente en la Figura 6. Por ello, si el equipo frigorífico no es capaz de suministrar 44,80 kW al principio del enfriamiento, no podremos enfriar el agua en 1 hora. Si rehacemos los cálculos considerando que instalamos un equipo de 24,42 kW, podemos ver que tardaríamos cerca de 1 hora y 50 minutos en enfriar el tanque.

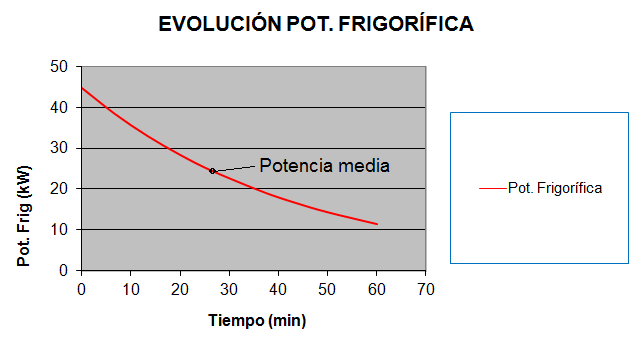
Figura 6

Figura 6. Evolución de la potencia frigorífica durante el proceso de enfriamiento.

La conclusión es que no basta con hacer un cálculo de la potencia media. Si queremos enfriar un fluido mediante serpentín sumergido en un tiempo concreto, hay que conocer la potencia máxima que necesitaremos. Como se ha podido ver, el Sistema 2 solo requiere un depósito y un serpentín, pero necesita de un equipo frigorífico de casi el doble de potencia para conseguir la misma velocidad de enfriamiento, además de una temperatura de refrigerante más baja. Por otra parte, el Sistema 1 implica instalar dos tanques y un grupo intercambiador externo, pero la potencia frigorífica es mucho menor y con una temperatura de refrigerante más alta. Habrá que analizar en cada caso concreto los costes de implantación y de explotación de cada sistema.

4. SISTEMA 3: ENFRIAMIENTO DE UN LÍQUIDO CON UN TANQUE Y UN INTERCAMBIADOR DE CALOR EXTERNO

Este método consiste en recircular el agua haciéndola pasar por un intercambiador externo y devolviéndola al tanque tras ser enfriada. Es quizás el problema más complejo de analizar de los vistos hasta ahora, ya que la temperatura del agua del tanque va disminuyendo progresivamente, y por tanto, la temperatura del agua que entra en el intercambiador de calor es variable, así como la temperatura de salida. Esto hace que, al igual que en el Sistema 2, el salto térmico entre el agua y el refrigerante sea variable (Figura 7).

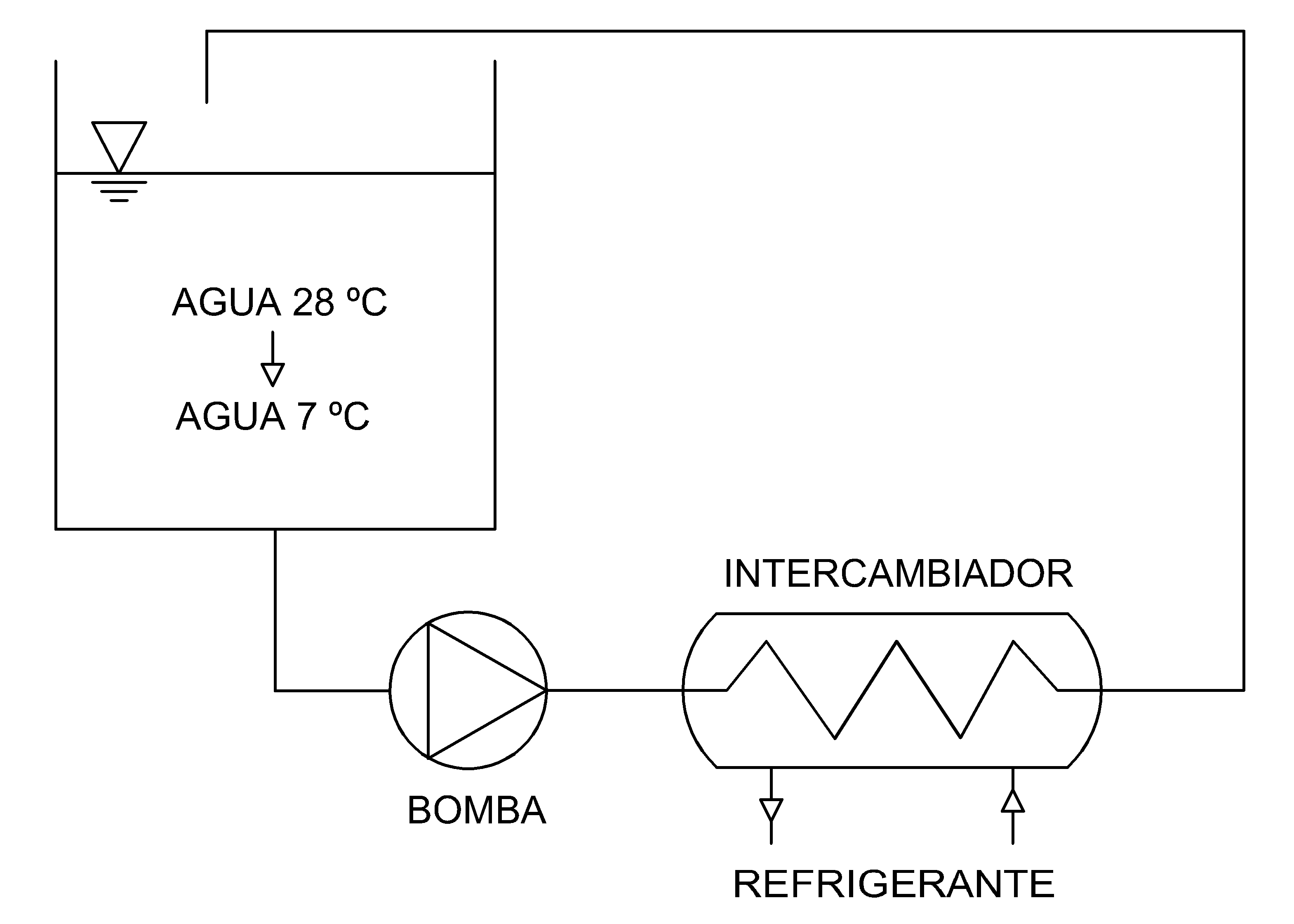Figura 7Figura 7. Esquema de enfriamiento mediante un tanque y un intercambiador de calor externo.

Las ecuaciones matemáticas que gobiernan este proceso son bastante complejas, y si alguien está interesado, puedo dedicar una entrada a este tema. No obstante, el resultado del análisis matemático permite obtener una fórmula bastante similar a la Ley de enfriamiento de Newton que vimos anteriormente, siendo la única diferencia en este caso que el coeficiente de transmisión de calor, K, va a ser sustituido por otro coeficiente, Γ, que depende de los caudales másicos de refrigerante y agua, además del propio coeficiente de transmisión del intercambiador, K (Ecuación 1).

(1) \begin{equation*} t=-\frac{\rho \cdot c \cdot V}{\Gamma \cdot S} \cdot \ln \left(\frac{T_{af}-T_{re} }{ T_{a0}-T_{r e}}\right)$ \end{equation*}

Siendo:

t, el tiempo de enfriamiento, en segundos

\rho, la densidad del agua = 1000 kg/m3

c, el calor específico del agua = 4186 J/kg ºC

V, el volumen de agua = 1 m<sup>3

\Gamma=\frac{K}{1+\frac{K\cdot S}{2} \cdot\left(\frac{1}{\dot{m}_{a}}+\frac{1}{\dot{m}_{r}}\right)}, coeficiente corregido donde:

K, es el coeficiente global de transmisión de calor del intercambiador = 3320 W/m2K (consideraremos que empleamos como refrigerante propilenglicol +  agua, en condiciones similares al Sistema 1 visto anteriormente. Os invito a probar con refrigerante R-134a para obtener otra variante).

Tenemos una serie de variables, desconocidas en principio, con las que podemos jugar en el software de cálculo del intercambiador para obtener el punto más favorable en equilibrio con la Ecuación 1 para el tiempo. Estas variables son:

\dot{m}_{a}, el caudal de agua (1000L en 1 hora) = ¿?

\dot{m}_{r}, el caudal de refrigerante = ¿?

S, la superficie de intercambio = ¿?

T_{re}, la temperatura de entrada del refrigerante = ¿?

Para comenzar a aproximarnos a la solución óptima, tomaremos un valor de Tre = 6 ºC, ya que es el más alto posible para poder enfriar a contracorriente agua hasta 7 ºC, y que ya empleamos en el Sistema 1. Tras tomar ese valor, usamos la Ecuación 1 y el software de simulación de SWEP, y comprobamos que el salto térmico entre el refrigerante y el agua es insuficiente, ya que, a diferencia del Sistema 1, en este caso el agua que va entrando al intercambiador está cada vez más fría, y esto hace que el tiempo de enfriamiento se alargue más de lo previsto. La única manera de poder usar refrigerante a 6 ºC sería aumentando enormemente los caudales de los fluidos en el intercambiador, así como la superficie del mismo, provocando un sobrecoste de bombeo e instalación. Por otra parte, podríamos dejar los caudales y la superficie de intercambio al mínimo, y bajar mucho la temperatura del refrigerante, pero eso supondría un gasto energético excesivo.

Nuestro objetivo final es conseguir enfriar el tanque en 1 hora. Tras varias iteraciones aproximativas, jugando con los caudales de refrigerante y agua, así como con la superficie del intercambiador y la temperatura del refrigerante, se puede llegar a una solución de equilibrio en cuanto a volumen de la instalación y gasto energético de la misma:

\dot{Q}, Potencia térmica intercambiada = 35,11 kW

T_{a0}, Temperatura inicial del tanque = 28 ºC

T_{af}, Temperatura final del tanque =7 ºC

T_{re}, Temperatura del refrigerante a la entrada = 2 ºC

\dot{m}_{a}, Caudal de agua = 0,4 kg/s

\dot{m}_{r}, Caudal de refrigerante = 1,77 kg/s

S, Superficie de intercambio = 1,96 m2

Conocidos estos resultados, es el momento de comparar los tres sistemas de enfriamiento analizados y ver las ventajas e inconvenientes de cada uno de ellos.

5. ESTUDIO COMPARATIVO DE LOS DIFERENTES SISTEMAS DE ENFRIAMIENTO DE LÍQUIDO

En la Tabla 1 se muestra de manera simplificada una comparativa de los tres sistemas. Para los tres casos se ha considerado que se emplea como refrigerante agua + propilenglicol al 20 %.Podemos ver que el Sistema 1 es el que tiene un mejor rendimiento energético desde el punto de vista frigorífico, y esto contribuye a menores gastos de explotación, aunque requiere de grupo de bombeo para agua y glicol. Por otra parte, se precisa de una costosa inversión inicial debido a que se emplean dos tanques de almacenamiento.

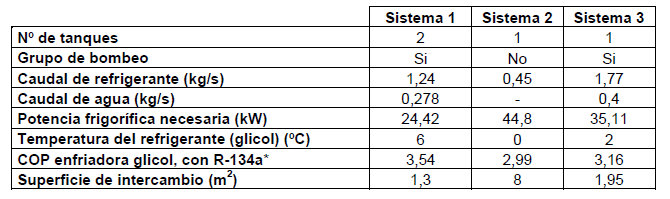
Tabla 1

Tabla 1. Comparativa de los tres sistemas de enfriamiento de líquidos (*Equipo de R-134a trabajando con Temperatura condensación 45 ºC, Recalentamiento y Subenfriamiento de 5 K).

El Sistema 2 es sin duda el más económico en cuanto a instalación inicial, sin necesidad de grupo de bombeo de agua, pero requiere un equipo frigorífico trabajando con un COP más bajo. Además, el coste debido a la superficie de intercambio es muy elevado en comparación con los demás sistemas. Esto es consecuencia del bajo coeficiente de transmisión, K, del serpentín sumergido. En cualquier caso, es un sistema muy empleado cuando el fluido a enfriar es de tipo alimentario (marmitas de caldo), y las labores de limpieza hacen difícil emplear intercambiadores de calor externos al depósito.

Por último, vemos que el Sistema 3, con recirculación del líquido a través de un intercambiador externo, es el más equilibrado en cuanto al coste de instalación y el consumo energético de los equipos, situándose en valores intermedios entre los dos sistemas anteriores. Este método de enfriamiento es muy empleado para enfriar rápidamente fluidos de proceso industrial, sobre todo si dicho fluido no presenta muchas impurezas que puedan obstruir el intercambiador de calor.

 

Fuente: CoolProyect

Etiquetas:

@amrandado

​about.me/amrandado

También te podría gustar...

Deja una respuesta

Descripción general de privacidad

Este sitio web utiliza cookies para que podamos brindarle la mejor experiencia de usuario posible. La información de las cookies se almacena en su navegador y realiza funciones como reconocerlo cuando regresa a nuestro sitio web y ayudar a nuestro equipo a comprender qué secciones del sitio web le resultan más interesantes y útiles.