| Sección |
Teoría |
Actividades |
Soluciones |
| 4.2 Interpretación geométrica de la derivada |
La derivada de una función en un punto coincide con la pendiente de la
recta tangente esa función en ese punto.
De donde se deduce que:
- Si f'(a) > 0 , la función es creciente en x = a.
- Si f'(a) < 0 , la función es decreciente en x = a.
- Si hay un máximo o mínimo relativo en x = a, entonces f'(a) = 0.
|
|
|
| 4.3 Reglas de derivación |
REGLAS DE DERIVACIÓN:
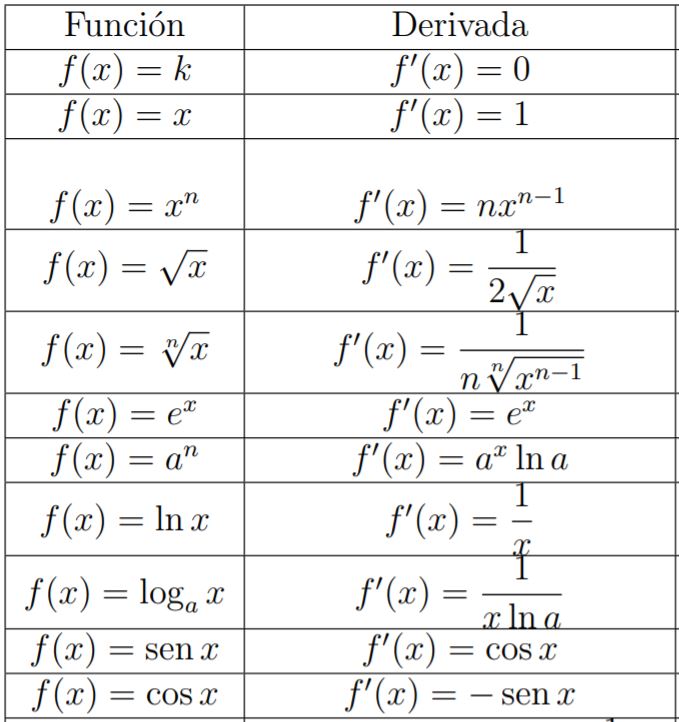
DERIVADA DE LAS OPERACIONES CON FUNCIONES:
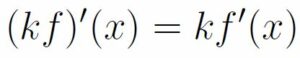
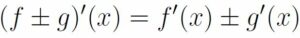
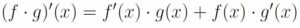
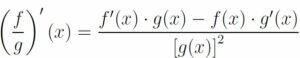
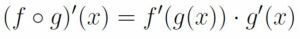
La regla de la cadena se aplica a la composición de funciones (cuando una función está dentro de otra) y lo que viene a decir es que primero se deriva la función que lo engloba todo (la que está más hacia fuera), dejando dentro de esta derivada lo que había dentro de la función, y luego se multiplica por la deriva de la función que estaba en el interior.

|
Ejercicios 1 y 2 de los apuntes |
 |
Ejercicio 1 |
 |
Ejercicio 2 |
|
| 4.4 Ecuación de la recta tangente |
Como ya hemos dicho, la derivada de una función en un punto coincide con la pendiente de la recta tangente a la función en dicho punto. Con lo cual, la ecuación de la recta tangente viene dada por:
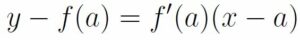
 
|
Ejercicio 3 de los apuntes |
 |
Ejercicio 3 |
|
| 4.5 Derivabilidad |
Para que una función sea derivable en un punto debe cumplirse las siguientes condiciones:
- Que f sea continua en x = a.
- Que las derivadas laterales coincidan.
Los puntos en los que estudiaremos la derivabilidad serán los mismos que en los que estudiábamos la continuidad, es decir, los puntos de cambio de trozo y los que anulen al denominador.
  
|
Ejercicios 4 y 5 de los apuntes |
 |
Ejercicio 4 |
 |
Ejercicio 5 |
|
| 4.6.1 Estudio de la monotonía (crecimiento y decrecimiento) |
Para estudiar la monotonía de una función seguiremos los siguientes pasos:
- Derivamos la función.
- Resolvemos la ecuación f'(x) = 0.
- Estudiamos los signos de f’. Si f'(a) > 0 , la función es creciente en x = a; y si f'(a) < 0 , la función es decreciente en x = a.
|
|
|
| 4.6.2 Estudio de los extremos (máximos y mínimos) |
Para estudiar los extremos basta con observar la monotonía.


|
Ejercicios 6 y 7 de los apuntes |
 |
Ejercicio 6 a, d, f |
 |
Ejercicio 7 |
|
| 4.6.3 Estudio de la curvatura (cóncava y convexa) |
Para estudiar la monotonía de una función seguiremos los siguientes pasos:
- Derivamos la función.
- Resolvemos la ecuación f»(x) = 0.
- Estudiamos los signos de f». Si f»(a) > 0, la función es convexa en x = a; y si f»(a) < 0, la función es cóncava en x = a.
|
Ejercicio 8 de los apuntes |
 |
Ejercicio 8 |
|
| 4.7 Observaciones
|
Recordemos que:
- Si f'(a) > 0 , la función es creciente en el punto x = a.
- Si f'(a) < 0 , la función es decreciente en el punto x = a.
- Si hay un máximo o mínimo relativo en x = a, entonces f'(a) = 0.
- La derivada de una función en un punto coincide con la pendiente de la ecuación de la recta tangente a la función en ese punto, m = f'(a).
- Si f’ ‘(a) > 0 , la función es convexa en x = a.
- Si f’ ‘(a) < 0 , la función es cóncava en x = a.
- Si hay un punto de inflexión en x=a, entonces f’ ‘(a) = 0.
|
Ejercicios 9 y 10 de los apuntes |
 |
Ejercicio 9 |
 |
Ejercicio 10 |
|
| RECOPILATORIO DE LA UNIDAD |
|
Esquema-resumen
 |
Ejercicios de derivadas :
|
Ejercicios 15a, 20 de la relación de ejercicios |
 |
Ejercicio 20 (relación) |
|
|
Ejercicios de recta tangente:
|
Ejercicio 2a, 6b, 8c, 11b, 21c de la relación de ejercicios |
 |
Ejercicio 11b (relación) |
|
|
Ejercicios de derivabilidad:
|
Ejercicios 4a, 9, 11a, 14a de la relación de ejercicios |
 |
Ejercicio 4a (relación) |
 |
Ejercicio 9 (relación) |
|
| |
Ejercicios de monotonía y extremos:
|
Ejercicios 1, 3, 4b, 5, 7, 8ab, 10, 12bc, 15b, 16, 17a, 19ab, 21a de la relación de ejercicios |
 |
Ejercicio 1 (relación) |
 |
Ejercicio 3 (relación) |
 |
Ejercicio 4b (relación) |
|
| |
Ejercicios de curvatura:
|
Ejercicios 13, 21b de la relación de ejercicios |
 |
Ejercicio 13b (relación) |
|
| |
Ejercicios de parámetros:
|
Ejercicios 2a, 6a de la relación de ejercicios |
 |
Ejercicio 22a (relación) |
|
| |
Ejercicios con todo mezclado:
|
|
 |
Ejercicio 2 (relación) |
 |
Ejercicio 6 (relación) |
|