| Sección |
Teoría |
Actividades |
Soluciones |
| 1.2. Operaciones con matrices |
Suma y resta:
- Deben tener la misma dimensión.
- Se suman o restan los elementos que ocupan la misma posición.
Producto:
- El número de filas de la segunda matriz debe coincidir con el número de columnas de la primera.
- El resultado tiene tantas filas como la primera matriz y tantas columnas como la segunda.
- Se «multiplica» cada fila de la primera por cada columna de la segunda.
Potencia:
- Calcular una potencia de una matriz NO es elevar a esa potencia cada elemento de la matriz.
- Se debe multiplicar la matriz por sí misma tantas veces como indique el exponente.
Traspuesta:
Se cambian los elementos de las filas por los de las columnas.
   
|
Ejercicios 2, 3, 4, 5, 6 de los apuntes |
 |
Ejercicio 2 |
 |
Ejercicio 3 (parámetros) |
 |
Ejercicio 4 (potencia) |
 |
Ejercicio 5 (parámetros) |
 |
Ejercicio 6 (potencia) |
|
| 2. Determinantes |
De orden 2:
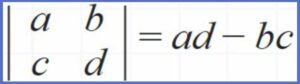
De orden 3:

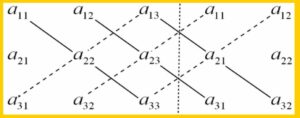
 
|
Ejercicios 7 y 8 de los apuntes |
 |
Ejercicio 7 |
 |
Ejercicio 8 |
|
| 3. Matriz inversa
3.1 Cálculo de la matriz inversa por la adjunta traspuesta |

 
|
Ejercicios 15, 16 y 17 (a, b y c) de los apuntes |
 |
Ejercicio 15 |
 |
Ejercicio 16 |
 |
Ejercicio 17 a, b y c |
|
| 4. Ecuaciones y sistemas matriciales
(Ecuaciones) |
- Despejamos la matriz incógnita (teniendo en cuenta que no existe la división de matrices).
- Realizamos las operaciones correspondientes.
 
|
Ejercicios 20, 21, 22 y 24 de los apuntes |
 |
Ejercicio 20 |
 |
Ejercicio 21 |
 |
Ejercicio 22 |
 |
Ejercicio 24 |
|
| 4. Ecuaciones y sistemas matriciales
(Sistemas) |
Un sistema de ecuaciones matriciales es un sistema en el que las incógnitas son matrices.
Para resolver sistemas lineales de ecuaciones matriciales se procede de la misma forma que para resolver sistemas de ecuaciones lineales, es decir, por los métodos de reducción, sustitución o igualación.
 
|
Ejercicios 18 y 19 de los apuntes |
 |
Ejercicio 18 |
 |
Ejercicio 19 |
|
| 5. Problemas con matrices |
|
Ejercicio 25 de los apuntes |
 |
Ejercicio 25 |
|
| 6.2 Método de Gauss para la resolución de sistemas |
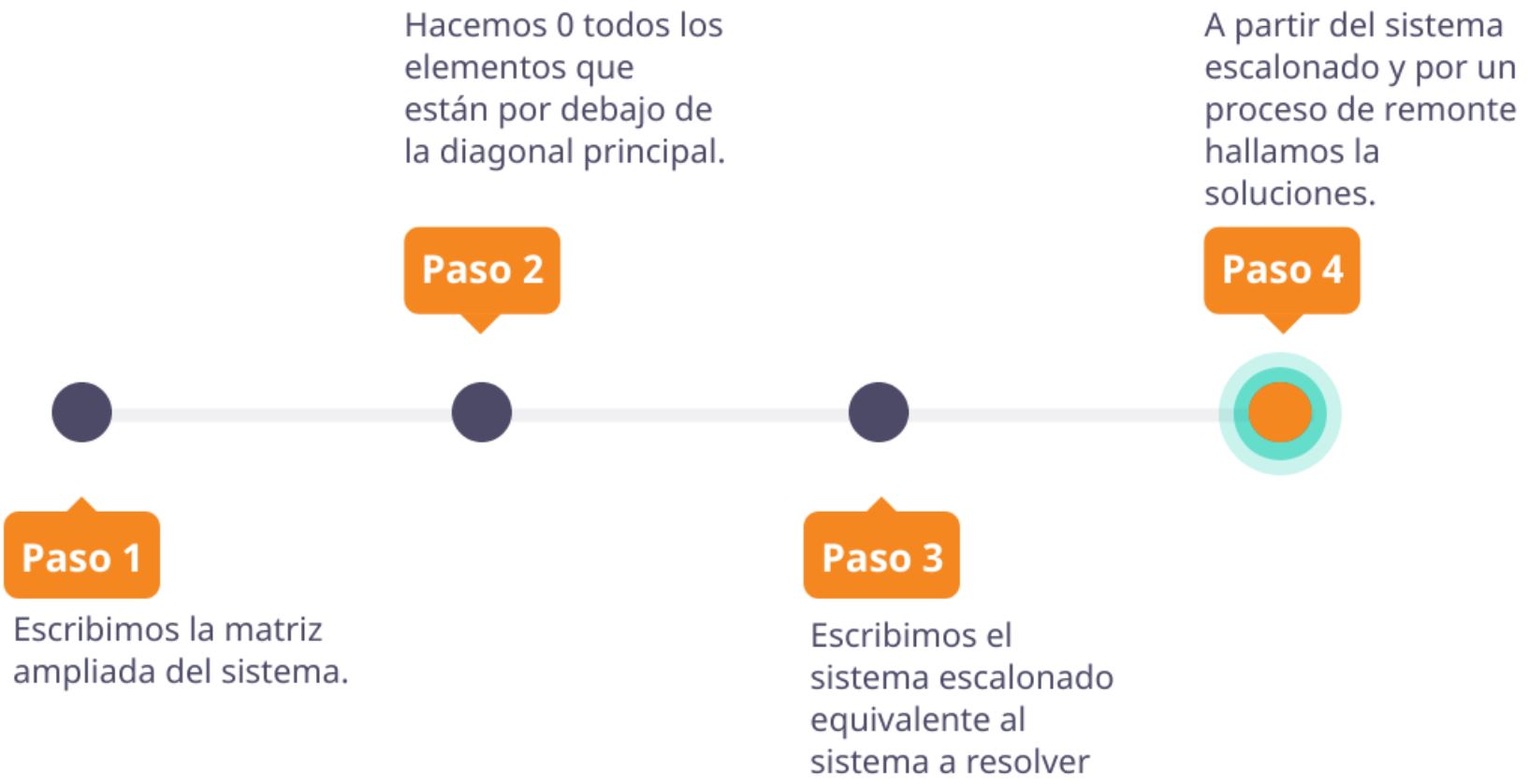
Para llevar a cabo el paso 2 podemos realizar las siguientes transformaciones: intercambio de dos filas, multiplicación o división de una fila por un número, realizar una combinación lineal de dos filas.

|
Ejercicio 26 de los apuntes |
 |
Ejercicio 26 |
|
| RECOPILATORIO DE LA UNIDAD |
Esquema-resumen
 |
Ejercicios de cálculo y comprobación de igualdades:
|
Ejercicios 8a, 10a, 11a, 20a y 24 a de la relación 1 de ejercicios |
 |
Ejercicio 8a (relación 1) |
 |
Ejercicio 10a (relación 1) |
|
|
Ejercicios de potencias de matrices:
|
Ejercicio 2a de la relación 1 de ejercicios |
 |
Ejercicio 2a (relación 1) |
|
|
Ejercicios de cálculo de parámetros:
|
Ejercicios 4a, 9b, 14a, 18, 19a, 21 y 23a de la relación 1 de ejercicios |
 |
Ejercicio 18 (relación 1) |
 |
Ejercicio 21 (relación 1) |
|
| |
Ejercicios de dimensiones de matrices (para la realización de operaciones):
|
Ejercicios 3b, 6b y c, 7a y 9a de la relación 1 de ejercicios |
 |
Ejercicio 3b (relación 1) |
 |
Ejercicio 6 b y c (relación 1) |
|
| |
Ejercicios de inversa:
|
Ejercicios 23b y 25a de la relación 1 de ejercicios |
 |
Ejercicio 23b (relación 1) |
 |
Ejercicio 25a (relación 1) |
|
| |
Ejercicios de ecuaciones matriciales:
|
Ejercicios 1b, 2b, 3a, 4b, 6a, 7b, 8b, 10b, 11b, 12, 14b, 15a, 19b, 20b, 24b y 25b de la relación 1 de ejercicios |
 |
Ejercicio 1b (relación 1) |
 |
Ejercicio 2b (relación 1) |
 |
Ejercicio 3a (relación 1) |
|
| |
Ejercicios de sistemas de ecuaciones matriciales:
|
Ejercicio 1a de la relación 1 de ejercicios |
 |
Ejercicio 1a (relación 1) |
|
| |
Problemas con matrices:
|
Ejercicio 5 de la relación 1 de ejercicios |
 |
Ejercicio 5 (relación 1) |
|