Operaciones Combinadas

¡Hola de nuevo!

Hoy os traigo un pequeño tutorial sobre las operaciones combinadas.

Antes de empezar debemos recordar que las operaciones combinadas eran una serie de cantidades numéricas en las que nos podíamos encontrar varias operaciones mezcladas. Si recordáis podían tener varios formatos, incluso algunas tenían paréntesis, lo cual nos extrañaba mucho al principio. Ejemplos de operaciones combinadas son los siguientes:

• 8 + 5 X 7 -1
• 9 + ( 7 X 5)
• 4 + (10 – 5) X 8

Para resolver este tipo de operaciones debemos seguir una serie de pasos. El primero de ellos es saber la jerarquía (importancia) u orden a la hora de ejecutarlos. Este orden de ejecución es muy importante porque no hacerlo correctamente nos llevaría a resultados erróneos.

El orden de jerarquía u orden en que debemos realizarlas es el siguiente:

• 1º Siempre realizar las operaciones que están dentro de los paréntesis (). Es la más importante de todas.
• 2º Si no hay paréntesis, o ya los hemos resuelto, debemos seguir con las multiplicaciones y/o divisiones.
• 3º Una vez terminado lo anterior, seguiremos con las sumas y/o restas.

Como siempre, todo esto que os acabo de explicar se ve mejor con un ejemplo. Vayamos a ello:

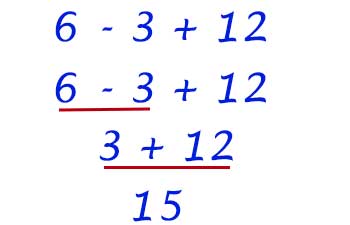
Primer paso: Buscamos un paréntesis y vemos que no hay, así que pasamos al siguiente paso.

Segundo paso: Buscamos si hay alguna multiplicación o una división. Vemos que tampoco las hay. Pasamos al siguiente paso.

Tercer paso: Vemos que está compuesta de una resta y una suma. Por lo que para resolverla, empezamos a realizar la operación de izquierda a derecha. Realizamos primero la resta que está en primera posición «6-3» igual a 3 y continuamos con la siguiente operación que es una suma, por lo que realizamos «3 + 12» igual a 15. Así hemos resuelto esta operación combinada.

En este ejemplo, se complica un poco el tema, no mucho, no vayamos a exagerar. Pero es evidente que hay dos operaciones que tienen diferente «jerarquía», o lo que es lo mismo, importancia.

Primer paso: No hay paréntesis, entonces nos saltamos este paso y seguimos con el siguiente:

Segundo paso: busco una multiplicación o una división. Veo que tenemos una multiplicación en esta combinada » 5 X 10″. Como sé que la multiplicación es más importante que la suma, la realizo en primer lugar, y da como resultado: 50.

Tercer paso: Sigo buscando multiplicaciones y divisiones, y veo que no me quedan más. Por lo que busco ahora sumas y/o restas, me encuentro una suma, así que realizo la suma correspondiente «6 + 50» igual a 56.

Este sería uno de los ejemplos donde entra en juego los paréntesis. Vamos a hacerlo paso a paso.

Primer paso: Tenemos en cuenta la jerarquía, y realizamos en primer lugar las operaciones que se encuentran dentro del paréntesis ( 9 – 4 ), lo que me da como resultado 5.

Segundo paso: Realizamos ahora la multiplicación, «8 X 5», igual a 40.

Tercer paso: ¡Sorpresa! Ya hemos terminado, porque no quedan más operaciones que realizar.

Si os dais cuenta, el paréntesis rompe la jerarquía de las operaciones. A pesar que la resta tiene menor importancia que la multiplicación, en las combinadas al ir encerradas entre paréntesis, rompe la jerarquía y la coloca por encima de la multiplicación. Es como una advertencia: ¡Cuidado! ¡Haz primero lo que te pongo entre paréntesis aunque las demás tengan mayor importancia!

Para finalizar os voy a colocar algunos ejemplos operaciones combinadas resueltos:

• 7 + 5 X 2 – 3 = 7 + 10 – 3 = 17 – 3 = 14
• 9 X (5 -2) + 8 = 9 X 3 + 8 = 27 + 8 = 35
• (5 + 2) + 4 + (2 – 1) =  7 + 4 + (2 – 1) = 7 + 4 + 1 = 11 + 1 = 12

Nos vemos en clase,

José Manuel.