☑%🍕Proporcionalidad y porcentajes 2º ESO
PROPORCIONALIDAD Y PORCENTAJES SECUNDARIA
En esta página hacemos un repaso con ejercicios interactivos de proporcionalidad para secundaria, aunque mucho conceptos sean de primaria.
INDICE
INDICE0. ¿De qué nos acordamos?
📖 Cómo crear fracciones equivalentes
☑Ejercicios on line de Fracciones Equivalentes
1. Razón y Proporción
☑Ejercicios on line de Magnitudes
2. Proporcionalidad Directa
📖 Ejercicios resueltos de tablas de proporcionalidad directa
🎥Tablas de proporcionalidad directa e inversa.🎥
☑Problemas de proporcionalidad directa
2.1. Método de reducción a la unidad
☑Problemas de proporcionalidad directa con reducción a la unidad
2.2. Método de regla de tres
🎥Problema de proporcionalidad directa.🎥
☑Problemas de proporcionalidad directa con regla de tres
3. Proporcionalidad Inversa
☑ Ejercicios de proporcionalidad inversa
3.1. Método de regla de tres inversa
🎥Problema de proporcionalidad inversa.🎥
☑Ejercicios de proporcionalidad inversa con regla de tres
🎥3.2. Repaso a la proporcionalidad. Video Troncho y Poncho.🎥
4. Porcentajes
📖 Calcular el porcentaje de un número.
☑Ejercicios de porcentaje de un número.
📖 Calcular el porcentaje de dos números.
☑Ejercicios calcular el porcentaje de una fracción.
4.1. Problemas de porcentajes.
📖 3 Tipos de problemas de porcentajes.
☑Ejercicios de problemas de porcentajes.
4.2. Problemas de aumentos y disminuciones porcentuales.
☑Ejercicios de problemas de resueltos de rebajas.
🎥4.3. Repaso de porcentajes. Videos.🎥
5. Regla de interés simple
📖 Calcular el intrés simple.
☑Ejercicios de cálculo de interés simple.
Objetivos
- Identificar las realciones entre magnitudes directa e inveramente proporcionales.
- Utilizar convenientemente las relaciones de proporcionalidad: factor de conversión, regla de tres, …
- Resolver problemas relacionados con la proporcionalidad.
- Usar porcentajes para resolver problemas en la vida cotidiana.
- Conocer recursos de internet para reforzar y ampliar conocimientos.
0. ¿De qué nos acordamos?
Para empezar
Para empezarAntes de empezar esta unidad debemos recordar unas cosillas:
◊ Cómo crear fracciones equivalentes.
◊ Cómo calcular la fracción de una cantidad.
Cómo crear fracciones equivalentes
Empezando de una fracción 
creamos otra multiplicando o dividiendo numerador y denominador por el mismo número.Veamos unos ejemplos:
Ejercicio resuelto 1
Dado 
De esta forma hemos obtenido 15/35 fracción equivalente a 3/7. Este método de conseguir fracciones equivalentes se llama amplificación de fracciones.
Ejercicio resuelto 2
Dado 
De esta forma hemos obtenido 6/5 fracción equivalente a 30/25. Este método de conseguir fracciones equivalentes se llama simplificación de fracciones.
Otra forma de tener una fracción equivalente es encontrar el número que falta 
.Para eso, usaremos la definición de fracción equivalente que dice 
Veamos un ejemplo:
Ejercicio resuelto 3
Vamos a buscar el número que falta 
, es decir, vamos a buscar la letra x.
Multiplicamos en cruz como en la definición y tenemos 5·30 = 25·x entonces 150 = 25·x.
Ahora qué número multiplicado por 25 da 150, dividimos para encontrarlo 150 entre 25, 150:25 = 6.
Resultado x = 6.
1.Razón y proporción
Para empezar
Definiciones
◊Magnitud según el diccionario de la lengua, propiedad física que puede ser medida, por ejemplo, la temperatura, el peso, la longitud, etc.
Está claro, si no se puede medir no es magnitud. Esto viene bien para razonar las actividades de después.
◊Razón según el diccionario de la lengua y después de elegir, cociente de dos números o, en general, de dos cantidades comparables entre sí.
Es decir, dadas dos magnitudes relacionadas a y b, la razón es .
Esta palabra tiene muchos significados incluso en matemáticas pero nos referimos a Razón de Proporcionalidad sin nada más.
◊Proporción según el diccionario de la lengua, igualdad de dos razones, es decir, y 
son iguales 
.
◊Proporcionalidad proporción de unas partes o magnitudes relacionadas entre sí.
Ejercicios on line de Magnitudes
Contesta pensando si son magnitudes los siguientes casos y así comprobar lo aprendido.
2. Proporcionalidad Directa.
Para empezar
Dos magnitudes son directamente proporcionales cuando la división entre las cantidades relacionadas da siempre el mismo número, eso quiere decir, que la relación es constante.
Ejercicios de tablas de proporcionalidad directa
Video de tablas de proporcionalidad
Ejercicio resuelto 1
Si cada kilo de manzanas vale 40 céntimos, averigua la relación que existe entre el peso de manzanas y el precio.
Para ello, formamos una tabla de dos filas: en una de ellas representamos las cantidades de una magnitud,y en la otra, las cantidades de la otra magnitud.
Todas las divisiones entre el precio de las manzanas y su peso dan el mismo resultado:
Entonces, las magnitudes son directamente proporcionales, y la constante de proporcionalidad es k = 40
Ejercicio resuelto 2
Considera un coche que no circula a velocidad constante, es decir, va frenando y acelerando según el tráfico, de forma que se obtengan los siguientes datos.
Realizamos todas las divisiones entre las dos magnitudes:
Podemos observar que estas divisiones no dan el mismo resultado.
Por tanto, las magnitudes de las horas transcurridas y los kilómetros recorridos no son directamente proporcionales.
Ejercicio de completar la tabla
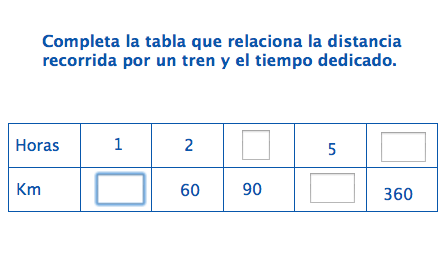
Completa la tabla relacionando magnitudes directamente proporcionales.
Ejercicio de completar la tabla
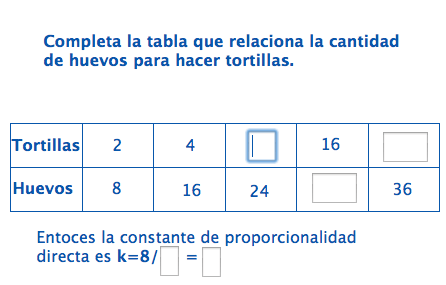
Completa la tabla relacionando magnitudes directamente proporcionales y encuentra la constante de proporcionalidad.
Identifica las afirmaciones verdaderas
Pincha si las afirmaciones son magnitudes directamente proporcionales.
2.1. Método de reducción a la unidad
Para empezar
En muchos problemas de la vida real se encuentran relaciones de dos magnitudes directamente proporcionales.
El método más sencillo es reducción a la unidad.
Pasos que hay que hacer:
1. Comprobar que las dos magnitudes son directamente proporcionales.
2. Encontrar el número que hay que reducir dividiendo por su valor en las dos magnitudes.
3. Multiplicar por el número correcto las dos magnitudes, para conseguir la solución.
Ejercicio resuelto
Dos kilos de naranjas cuestan 1,50 €. ¿Cuánto costarán 5 kg? ¿Y 12 kg?
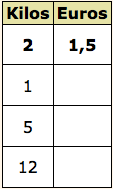
Pasos:
1. Comprobación. Está claro, el precio de las naranjas viene fijado por la cantidad de naranjas que compre. Cuantos más kilos de naranjas compre mayor precio tendrá.
Entonces las dos magnitudes son directamente proporcionales.
2. Para encontrar el precio de 5 kilos de naranjas antes deberemos calcular el precio de 1 kilo.
Para eso dividiremos, en este caso, por 2 el número de kilos de naranjas con precio conocido.
3. Multiplicamos por 5 para saber el precio de 5 kilos y por 12 para saber el precio de 12 kilos, y así conseguir la solución.
SOLUCIÓN: 5 Kilos de naranjas cuestan 3,75 euros y 12 kilos cuestan 9 euros.
Ejercicio Interactivo
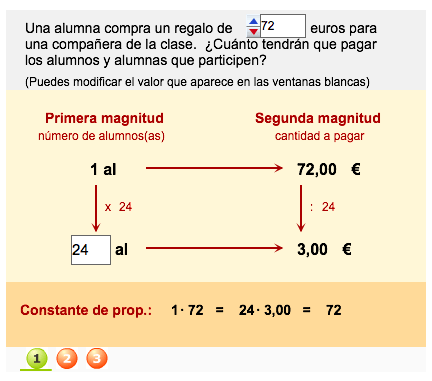
Completa la tabla relacionando magnitudes de proporcionalidad directa por el método de reducción a la unidad.
Ejercicio on line
Completa la tabla por el método de reducción a la unidad.
Ejercicio on line
Completa la tabla por el método de reducción a la unidad.
2.2. Método de regla de tres
Para empezar
Hemos visto en el punto anterior una forma de resolver problemas de la vida real de proporcionalidad directa.
Ahora veremos otro más rápido y sencillo, es Método de regla de tres.
Pasos que hay que hacer:
1. Expresar el problema en forma de fracciones igualadas.
2. Multiplicar en cruz.
3. Despejar la incognita x para hallar su valor.
Ejercicio resuelto
Doscientos gramos de mortadela cuestan 1,75 €. ¿Cuánto costará 700 gr?
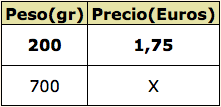
Pasos:
Paso 1. Expresar en forma de fracción.
Cada columna una fracción.
Paso 2. Multiplicar en cruz.
Paso 3. Despejamos la X para encontrar su valor.
Redondeando nos queda 6,13 euros
SOLUCIÓN: 700 gramos de mortadela cuesta 6,13 euros.
Ejercicio de refuerzo
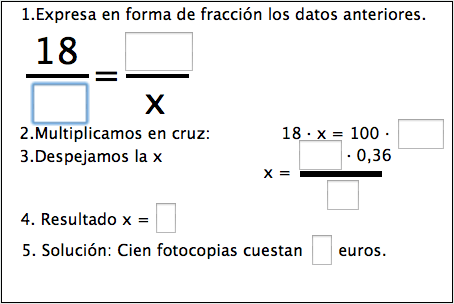
Resuelve por el método de regla de tres.
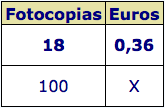
El precio de 18 fotocopias es de 0,36 €. ¿Cuánto costará hacer 100 fotocopias?
(completa el ejercicio on line)
Ejercicios de repaso de proporcionalidad directa
Proprocionalidad Directa. Método de regla de tres.
1. Practica la mecánica de la regla de tres y la resolución de problemas [HTML].
2. Practica la resolución de problemas de proporcionalidad directa [FLASH].
3. Practica resolviendo problemas de la regla de tres directamente proporcionales [HTML].
3. Magnitudes inversamente proporcionales
Para empezar
Dos magnitudes son inversamente proporcionales,cuando al crecer una la otra disminuye en la misma proporción, o al decrecer la primera la segunda aumenta en la misma proporción.
Esto hace que la multiplicación de las dos magnitudes nos de siempre el mismo valor. La constante de proporcionalidad inversa.
Ejercicio resuelto
Si un coche se mueve a 10 km/h de velocidad y tarda 120 minutos en llegar al siguiente pueblo, averigua la relación que existe entre velocidad y tiempo.
Para ello, formamos una tabla de dos filas: en una de ellas representamos las cantidades de una magnitud, y en la otra, las cantidades de la otra magnitud.
Todas las multiplicaciones entre velocidad y tiempo dan el mismo resultado:
Entonces, las magnitudes son inversamente proporcionales, y la constante de proporcionalidad inversa k = 1200 .
Ejercicio resuelto
Veamos un ejemplo de como funciona las magnitudes inversamente proporcionales, como al cambiar el número de una magnitud, la otra cambia, pero siempre la constante de proporcionalidad inversa permanece fija.
Ejercicio de repaso
Relena los huecos correctamente.
3.1. Método de regla de tres inversa
Para empezar
Hemos visto antes la regla de tres pero en situaciones de proporcionalidad directa, muy bien pues vamos a ver lo mismo pero en proporcionalidad inversa.Ahora aprenderemos la forma más sencilla, método de regla de tres inversa.
Pasos que hay que hacer:
0. Plantear el problema.
1. Expresar el problema en forma de fracciones igualadas.
Pero cambiando el orden de la magnitud de la incognita x.
2. Multiplicar en cruz.
3. Despejar la incognita x para hallar su valor.
VIDEO DE PROPORCIONALIDAD INVERSA
Ejercicio resuelto
Sabiendo que dispongo de una determinada cantidad de dinero y que con ella puedo comprar 4 camisetas a 9 € cada una. ¿Cuántas camisetas podría comprar si me costaran 12 € cada una?
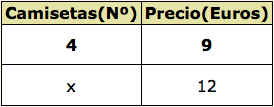
1. Expresar en forma de fracción. Cada columna una fracción.
Y cambiamos la x por 4.
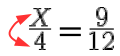
2. Multiplicar en cruz.
3. Despejamos la X para encontrar su valor.
Nos queda 3 camisetas
SOLUCIÓN: Si me costaban 12 euros cada camiseta podía comprar 3 camisetas.
Ejercicio de proporcionalidad inversa
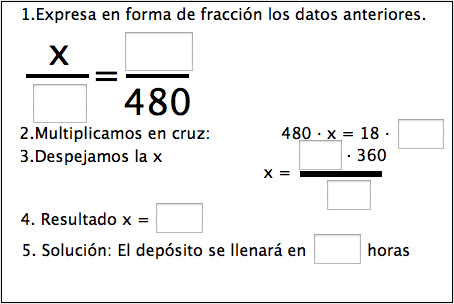
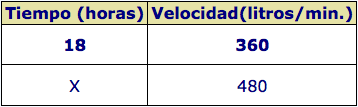
Un depósito de agua se llena en 18 horas con un grifo del que salen 360 litros de agua cada minuto.
¿Cuánto tardaría en llenarse el depósito si salieran 480 litros por minuto?
Ejercicio de refuerzo
Una fortaleza sitiada tiene víveres para 500 hombres durante tres meses.
¿Cuánto tiempo podrán resistir con ración normal de comida si se incorporan 150 hombres?
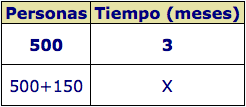
Solución: 650 personas tienen comida para ? meses.
PIENSA LA RESPUESTA
Ejercicio de repaso
Si ves que este método un poco difícil practica resolviendo 5 problemas de la regla de tres inversa en este enlace.
3.2. Repaso de Proporcionalidad
Video de Troncho y Poncho de proporcionalidad
Visualiza este video y repasaremos de forma diferente los conceptos de magnitud, proporcionalidad directa e inversa.
4. Porcentajes
Para empezar
Un porcentaje o tanto por cien se puede ver como una proporción, como una fracción o como un número decimal.
Ejemplo
El 20% es una proporción de 20 partes de una magnitud entre 100 partes de otra.
El 
(20 partes de 100).
El 20% = 0,20 (resultado de la división de la fracción)
Calcular el porcentaje de una cantidad
Para calcular un tanto por ciento de un número, se multiplica la cantidad por el tanto y se divide entre 100, es decir,
El porcentaje a% de n => 
Ejercicio resuelto
Calculamos el 40% de 50.
40% de 50 =>
Calcular el porcentaje de dos números
En ocasiones nos interesa saber el porcentaje, por ejemplo,
en una clase de 20 alumnos saber el porcentaje de los que van de excursión sabiendo que son 12.
Entonces para calcular el porcentaje realizamos la división
(los que van de excursión entre toda la clase)
12 : 20 = 0,60
Nos da 0,60 pero como sabes que un número decimal es un porcentaje entonces sabemos que
0,60 = 60%
Solución: El 60% de la clase va de excursión.
Ejercicios de Cálculo de porcentajes de una fracción
Practica el cálculo de porcentajes partiendo de fracciones
4.1. Problemas de porcentajes.
Para empezar
En muchas situaciones de la vida utilizamos el porcentaje.
Aparecen tres elementos: una parte del total, el total, y el tanto por ciento.
Hay tres tipos de problemas importantes:
a) Problemas de solucionar un parte del total.
b) Problemas de hallar el total.
c) Problemas de calcular el tanto por cien.
Problemas de calcular una parte del total
Ejercicio resuelto
En un equipo de baloncesto son 15 fichas pero están ocupadas el 80%.
¿cuántas fichas están ocupadas?
Entonces el 80% de 15 =>
Por tanto están ocupadas 12 fichas del equipo de baloncesto.
Ejercicio resuelto
El 44% alumnos de una clase de 25 participa en un concurso de ajedrez.
¿cuántos alumnos son?
Entonces el 44% de 25 =>
Por tanto 11 son los alumnos participantes.
Problemas de calcular el total
Ejercicio resuelto
En una carrera popular 5 kilómetros es el 80% de la prueba.
¿Cuántos kilómetros tenía toda la carrera?
Entonces 5 es el 80%
en este caso «es» significa dividir
=>
La carrera tiene en total 6,25 Kilómetros.
Ejercicio resuelto
Doce alumnos de una clase que son el 40% les gusta leer libros de aventuras.
¿cuántos alumnos son toda la clase?
Entonces el 12 es el 40%
Por tanto 30 son todos los alumnos de la clase.
Problemas de calcular el tanto por cien
Ejercicio resuelto
En un instituto de 300 alumnos se van de excursión el alumnado de segundo que son 81 alumnos.
¿Qué tanto por cien de alumnado se fue de excursión?
Para poder calcular el porcentaje tenemos que tener en cuenta la relación entre alumnado que va de excursión y todo el alumnado.
Esa relación es un división, de la siguiente forma:
(la parte entre el todo)
Solución el 27% del alumnado va de excursión.
4.2. Problemas de aumentos y disminuciones porcentuales
Para empezar
Una de las aplicaciones más frecuentes de los porcentajes en nuestra vida cotidiana son los descuentos o rebajas.
Partiendo de un precion inicial se produce un descuento de una parte del precio asociado a un tanto por cien.
También es muy común el uso de porcentajes asociado a impuestos, produciendo un incremento del precio de ciertos productos.
Disminuciones porcentuales. Rebajas
Vamos a ver unos ejemplos de descuentos o rebajas porcentuales.
Ejercicio resuelto 1
Unas zapatillas deportivas cuestan 45 euros. Si tienen un descuento de el 18%.
¿Cuánto costarán las zapatillas?
Vamos a resolver este tipo de problemas con la regla de tres.
1. Primero descontamos el porcentaje rebajado para saber el porcentaje que vamos a pagar.
100% – 18% = 82%. Ahora sabemos que vamos a pagar el 82% del producto.
2. Resolvemos como una proporcionalidad directa con regla de tres.
, multiplicamos en cruz y obtenemos 
despejamos la x
Solución: Las zapatillas cuestan 36,90 euros.
Ejercicio resuelto 2
Un cine ha vendido 1400 entradas en la semana del estreno de una pelicula. El gerente estima que en la segunda semana venderá un 20% menos.
¿Cuántas entradas espera vender en la segunda semana?
1. Primero descontamos el porcentaje del descenso de entradas.
100% – 20% = 80%. Sabemos que la entrada va a ser del 80%.
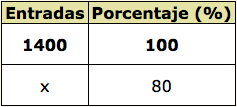
2. Resolvemos como una proporcionalidad directa con regla de tres.
, multiplicamos en cruz y obtenemos 
,
despejamos la x
Solución: En la segunda semana abrá una asistencia de 1120 espectadores.
Disminuciones porcentuales. Antes del precio rebajado.
Vamos a explicar un ejemplo en el que queremos saber el precio de algo después de la rebaja.
Se resolverá de una forma muy similar a la anterior.
Ejercicio resuelto
Una camiseta cuesta 12 euros. Ya rebajada un 30%.
¿Cuánto costaba la camiseta antes de la rebaja?
Vamos a resolver este tipo de problemas con la regla de tres.
1. Primero descontamos el porcentaje.
100% – 30%= 70%. Sabemos que el precio rebajado va a ser del 70%
2. Resolvemos como una proporcionalidad directa con regla de tres.
, multiplicamos en cruz y obtenemos 
,
despejamos la x
Solución: La camiseta costaba 17,14 euros.
Aumentos porcentuales.
Ejercicio resuelto
Un agricultor recogió en la campaña pasada 180 toneladas de tomates, pero este año espera un 25% más.
¿Cuántas toneladas espera cosechar este año?
1. Primero calculamos el porcentaje de aumento.
100% + 25%= 125%. Sabemos que va a ser del 125%.
2. Resolvemos como una proporcionalidad directa con regla de tres.
, multiplicamos en cruz y obtenemos 
,
despejamos la x
Solución: Este año espera cosechar 225 toneladas de tomates.
Aumentos porcentuales. Antes del incremento
Vamos a explicar un ejemplo en el que queremos saber el precio de algo después del incremento.
Se resolverá de una forma muy similar a la anterior.
Ejercicio resuelto
Una caja de 12 cartones de leche cuesta 9,50 euros con el 20% de impuestos incluido.
¿Cuánto costaba la caja de leche antes del incremento?
Vamos a resolver este tipo de problemas con la regla de tres.
1. Primero añadimos el porcentaje.
100% + 20%= 120%. Sabemos que el precio va a ser del 120%
2. Resolvemos como una proporcionalidad directa con regla de tres.
, multiplicamos en cruz y obtenemos 
,
despejamos la x
Solución: La caja de leche costaba 7,91 euros.
Problemas de rebajas y aumentas porporcionales
Realiza una actividad de cada tipo en tu cuaderno y al final comprueba el resultado
4.3. Repaso de porcentajes.
Repaso a los porcentajes
Visualiza este video y repasaremos los porcentajes.
Video Ejercicio de porcetajes
Una de mates: matemáticas en el súpermercado
Presta atención a este video y haz las cuentas para demostrar las diferencias entre las tres ofertas del supermercado.
5. Proporciones de la vida cotidiana. Regla de interés simple
Para empezar
Los problemas de proporcionalidad está muy presentes en nuestra vida cotidiana.
Es por ello, vamos a centrarnos en un tipo de problema de nuestra sociedad, los problemas de regla de interés simple.
Si depositamos un capital C en un banco durante un año, el banco nos dará un interés i, que se obtiene aplicando un porcentaje r%,
llamado rédito.
Si depositamos el capital durante t años, el interés se calculará con la fórmula:
Recordamos:
C: Capital.
r: % de rédito.
t: Tiempo en años.
i: interés o beneficio conseguido.
Si el tiempo se mide en meses entonces la fórmula cambia:
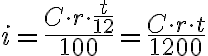
Esto ocurre porque pasamos el tiempo a años ya que el rédito es anual y para pasar a años debemos dividir por 12 el tiempo.
Recordamos:
C: Capital.
r: % de rédit.
t: Tiempo en meses.
i: interés o beneficio conseguido.
Ejercicios resueltos
Ejercicio resuelto 1
Calcular el interés que produce un capital de 1600 euros colocado a un interés simple del 3,5% durante 4 años.
Recordamos:
C = 1600
r = 3,5%
t = 4 años.
i = ?
Ejercicio resuelto 2
Calcular el interés que produce un capital de 5800 euros colocado a un interés simple del 4,5% durante 21 meses.
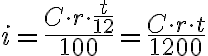
Recordamos:
C = 5800
r = 4,5%
t = 21 meses.
i = ?
Ejercicios on line de Interés Simple
Realiza las actividades guiadas paso a paso y así reforzar el aprendizaje de este tipo de problemas.
Pincha en la imagen.
Actividades aplicadas a la vida cotidiana [AMPLIACION]
Realiza los siguientes ejercicios como se explica en la web.
Enlaces de interés:
