TABLAS DE PROPORCIONALIDAD
INDICE
0.Preguntas Previas:
¿Qué es una tabla de proporcionalidad?
¿Cómo se calcula la tabla de proporcionalidad?
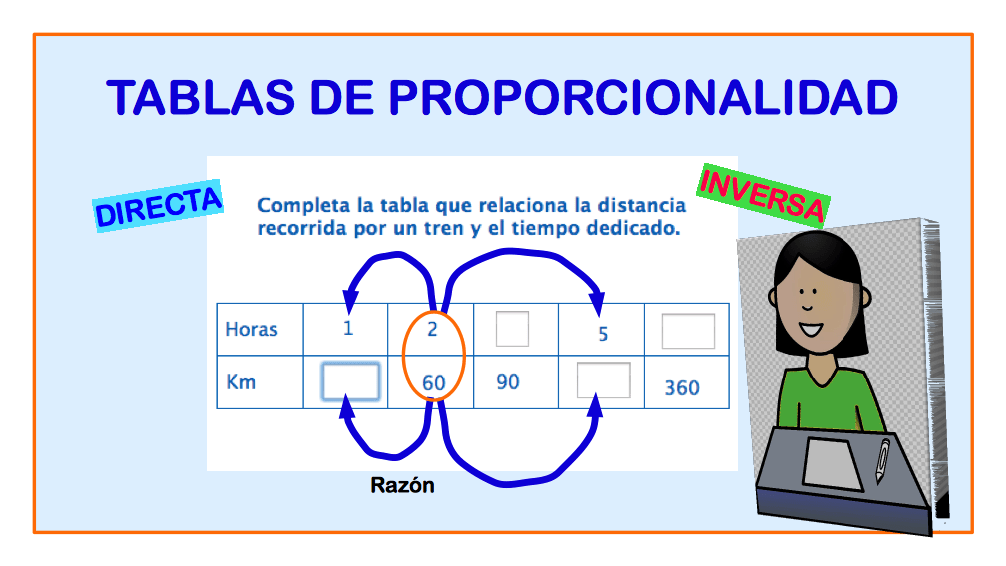
1. Tablas de Porporcionalidad Directa. Completa las siguientes tablas de proporcionalidad
📖 Ejercicio 1.Tablas de Proporcionalidad Directa
📖 Ejercicio 2.Tablas de Proporcionalidad Directa
📖 Ejercicio 3.Tabla de Proporcionalidad Directa
📖 Ejercicio 4.Tabla de Proporcionalidad Directa
☑🖱️ Ejercicio interactivo de Tabla de Proporcionalidad Directa
🎥Video de un Problema de Proporcionalidad Inversa🎥
¿Qué es una tabla de proporcionalidad?
Dada una tabla de valores numéricos que relacionan dos magnitudes: Alto y Ancho de un cuaderno, precio y peso de una fruta, velocidad y tiempo en el movimiento de una bicleta,o número de vacas y tiempo que tardan en consumir su pasto, … nos encontramos que esa relación es directa cuando las dos magnitudes crecen o decrecen ambas a la vez de forma proporcional.
| Peso en Kilogramos de Manzanas | 0,5 | 1 | 2 |
| Precio en monedas | 2$ | 4$ | 8$ |
Podemos ver que cuando crece el peso (el doble) crece el precio también (el doble) y cuando baja (a la mitad) eso pasa a ambas magnitudes a la vez.
Pero en otras ocasiones tenemos una relación inversa de proporcionalidad cuando una magnitud crece el doble y la otra baja la mitad, crece el triple y la otra baja la un tercio.Ejemplo. En una ganadería de vacas el consumo del pienso almacenado sigue esta tabla, en función al número de vacas.
| Número de vacas | 1 | 2 | 3 |
| Tiempo en días | 12 | 6 | 4 |
Como es lógico un recurso limitado como es el alimento de las vacas dura más cuantas menos vacas hay.
Si hay 1 vaca dura el pienso 12 días.
Si hay 2 vacas dura el pienso 6 días.
Si hay 3 vacas dura el pienso 4 días.
puede observarse que cuando aumenta el número de vas disminuye el número de días de forma proporcional inversa.
¿Cómo se calcula la tabla de proporcionalidad?
Si la tabla es directamente proporcional los métodos utilizados son:
- Método de reducción a la unidad donde sabiendo por ejemplo cuanto cuesta 1 kilogramo de fruta, puedo saber cuanto cuesta cualquier cantidad sin problemas.
- Método de regla de tres
Kilogramos Peras 2 X Monedas 1,5$ 6$ Para calcular el valor de X expresamos la tabla como igualdad de fracciones equivalentes, es decir, 2/X= 1,5/6, despejando la X obtenemos X=2×6/1,5 = 12/1,5 = 8. Así podemos calcular cualquier valor de tabla desconocido.
Si la tabla es inversamente o indirectamente proporcional los métodos utilizados son:
- Cálculo de la razón inversa
Si sabemos que al multiplicar a x b = r obtenemos la razón. Esa razón es identica para todo par de magnitudes de la tabla. Con esa información nos será muy sencillo calcular los valores que faltan en la tabla. - Método de regla de tres inversa
Para recorrer una cierta distancia, un ciclistaVelocidad (m/s) 12 30 Tiempo (s) 300 X Para calcular el valor de X expresamos la tabla como igualdad de fracciones equivalentes pero invirtiendo los valores realcionados con la X, es decir, 12/30= X/300, despejando la X obtenemos X=12×300/30 = 120. Así podemos calcular cualquier valor de tabla desconocido.
TABLAS DE PROPORCIONALIDAD DIRECTA
En estas tablas tenemos una relación entre las magnitudes que hace que cuando una suba de valor la otra magnitud también suba. Y cuando una baje su valor la otra también pero no de cualquier forma.
Ejemplo por reducción a la unidad
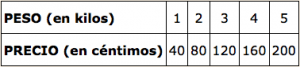Se ve que cuanto más aumenta el número de kilos de manzanas más aumenta su precio en céntimos.
Si el número de kilos aumenta el doble (x2) entonces el precio también aumenta el doble (x2).
Si el número de kilos aumenta el triple (x3) entonces el precio también aumenta el triple (x3).
Completa las siguientes TABLAS DE PROPORCIONALIDAD
✍️Ejercicio de Proporcionalidad Directa 1
Escribe el ejercicio en un papel e intenta encontrar la solución sin mirar. Si tienes dudas mira
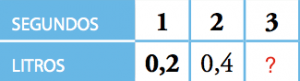
La tabla relaciona el tiempo que está abierto un grifo con la cantidad de agua que echa.
¿cuál es el agua arrojada a los 3 segundos?SOLUCIÓN
Por el Método de Reducción a la Unidad
Si 1 segundo echa 0,2 litros entonces 3 segundos que es el triple de tiempo arroja el triple de agua que es 0,6 liros.
El agua arrojada a los tres segundos es 0,6 litros.Si tienes dudas deja un comentario.
¿cuál es el agua arrojada a los 3 segundos?✍️Ejercicio de Proporcionalidad Directa 2
La tabla relaciona el tiempo en minutos que está abierto un grifo con la cantidad de agua que echa.
Otro grifo echa 3 L de agua en 1 minuto.
¿Cuántos arrojará en 6 minutos?SOLUCIÓN
Por el Método de Reducción a la Unidad
Si en 1 minuto echa 3 litros entonces en 6 minutos que es seis veces más (x6) de tiempo arroja el seis veces más agua siendo 18 litros.
El agua arrojada en seis minutos es 18 litros.Si tienes dudas deja un comentario.
Otro grifo echa 3 L de agua en 1 minuto.
✍️Ejercicio de Proporcionalidad Directa 3
¿Cuántos kilómetros recorrerá en 5 horas?
SOLUCIÓN de 1 hora
Por el Método de Regla de Tres.
En este caso aplicaremos el método de la regla de 3.
Lo escribimos como igualdad de fracciones.
75/x = 3/1 multiplicando en cruz como hemos señalado antes y obtenemos:3 · x = 75 · 1 que es lo mismo que 3·x = 75
¿Qué número multiplicado por 3 nos da 75?
Hacemos la división 75 : 3 = 25
Por tanto, x = 25.
SOLUCIÓN: En un hora el clicista recorrerá 25 kilómetros.
SOLUCIÓN de 5 horas
Por el Método de Reducción a la Unidad
Si sabemos por el apartado anterior que en 1 hora el ciclista ha recorrido 25 km.
Entonces por el método de reducción a la unidad podemos deducir que en 5 horas el ciclista recorrerá 25 · 5 = 125.
SOLUCIÓN: En 5 horas el clicista recorrerá 125 kilómetros.
Lo escribimos como igualdad de fracciones.
✍️Ejercicio de Proporcionalidad Directa 4
En esta tabla se relacionan dos magnitudes A y B directamente proporcional.
Vamos a calcular los valores de C, D, E, y F.SOLUCIÓN de C
Por el Método de Reducción a la Unidad
Como 2 valor la magnitud A corresponde a 6 valor la magnitud B.
Al relacionar 1 de la magnitud A estamos dividiendo la magnitud a entre 2 (:2).
Entonces también dividimos enre 2 la magnitud B y nos da de resultado: 6:2 = 3.
Por tanto, C = 3.SOLUCIÓN de D
Por el Método de Regla de tres.
En este caso aplicaremos la regla de 3.
Si A vale 2, entonces B vale 6, si A vale 3 entonces B vale D.
Lo escribimos como igualdad de fracciones.
2/6 = 3/D multiplicando en cruz como hemos señalado antes obtenemos:2·D=3·6 que es lo mismo que 2·D=18
El número multiplicado por 2 nos da 18 es el 9.
Por tanto, D = 9.
SOLUCIÓN de E
Por el Método de Reducción a la Unidad
Como 2 valor la magnitud A corresponde a 6 valor la magnitud B y también sabemos que 1 valor la magnitud A corresponde a 3 valor la magnitud B.
Entonces podemos multiplicar estos dos valores por 5 (x5) y obtenemos 3×5=15, lo esperado, y 1 x 5 = 5.Por tanto, E = 5.
Si tienes dudas deja un comentario.
SOLUCIÓN de F
Por el Método de Regla de 3.
En este caso aplicaremos la regla de 3.
Si A vale 2, entonces B vale 6, si A vale 10 entonces B vale F.
Lo escribimos como igualdad de fracciones.
2/6 = 10/F multiplicando en cruz como hemos señalado antes obtenemos:2·F=10·6 que es lo mismo que 2·D=60
El número multiplicado por 2 nos da 60 es el 30.
Por tanto, F = 60.
Si tienes dudas deja un comentario.
Vamos a calcular los valores de C, D, E, y F.
