02 TRAZADO DE POLÍGONOS repaso 1bach
03 TRANSFORMACIONES GEOMÉTRICAS DT2
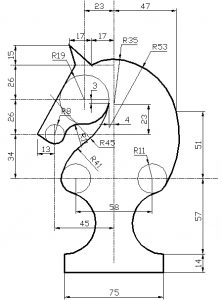
EJERCICIO TANGENCIAS (CABALLO DE AJEDREZ)
Ejercicio resuelto de tangencias paso a paso.
https://www.mongge.com/ejercicios/10689
CURVAS TÉCNICAS
Curvas cíclicas
Trazado de la cicloide.
La cicloide es una curva plana, lugar geométrico de las posiciones de un punto P perteneciente a una circunferencia O que rueda (sin resbalar) sobre una recta dada. La recta recibe el nombre de directriz y la circunferencia de generatriz o ruleta.Dada la circunferencia de centro O y la recta r, para trazar la cicloide dibujaremos la circunferencia tangente en P a la recta y a partir de él rectificaremos sobre r la circunferencia. Dividimos la circunferencia y su rectificación en un mismo número de partes iguales, doce en la ilustración, trazando normales y paralelas a la directriz por las divisiones de la recta y circunferencia respectivamente.En las intersecciones de las perpendiculares a r y la paralela que pasa por O están las posiciones del centro de la circunferencia O, que gira sobre r, cuando los radios de las divisiones de la generatriz coinciden con sus correspondientes divisiones en la directriz, O1, O2, O3… Con centro en O1 y el radio de la circunferencia generatriz en todo caso, trazamos un arco hasta cortar en P1 a la paralela que pasa por 1, con centro en O2 obtenemos P2 en la paralela que pasa por 2 y así sucesivamente. Los puntos así obtenidos se unen a mano alzada o con plantilla de curvas quedando de este modo trazada la curva.
Trazado de la cicloide
Trazado de la epicicloide.
La epicicloide es una curva plana, lugar geométrico de las posiciones de un punto P perteneciente a una circunferencia O’, generatriz, que rueda exteriormente sobre otra O o directriz. Dibujamos las dos circunferencias tangentes entre sí y para su trazado se procede de igual forma que en el ejercicio anterior pero trazando circunferencias concéntricas en lugar de rectas paralelas a la directriz y calculando la rectificación inversa de la longitud de la circunferencia generatriz sobre la circunferencia directriz.
Trazado de la hipocicloide.
La hipocicloide es una curva plana, lugar geométrico de las posiciones de un punto P perteneciente a una circunferencia O’, o generatriz, que gira interiormente sobre otra O, o directriz. Trazamos la circunferencia directriz tangente interior a la generatriz dada y para su trazado procedemos de idéntica forma que en el ejercicio precedente.
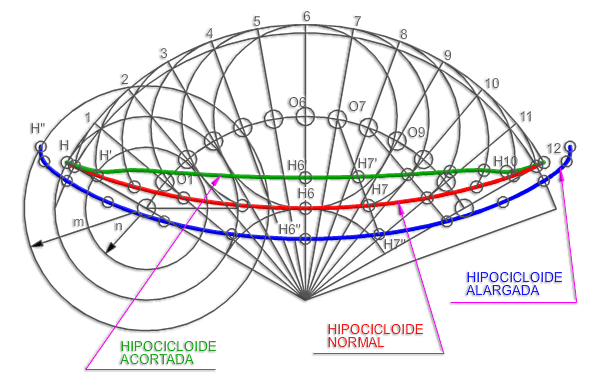
HIPOCICLOIDE RECTILÍNEA.
Cuando el diámetro de la generatriz es igual al radio de la directriz, la hipocicloide resultante es un segmento igual al diámetro de la directriz que contiene al punto de tangencia entre las dos circunferencias.
HIPOCICLOIDE TRIANGULAR.
Se produce esta curva cuando el diámetro de la generatriz mide un tercio del diámetro de la directriz.
HIPOCICLOIDE CUADRANGULAR
Se produce esta curva de cuatro lazos cuando el diámetro de la generatriz mide la cuarta parte del diámetro de la directriz. Se denomina Astroide.
Trazado de la pericicloide.
La Pericicloide es una curva plana, lugar geométrico de las posiciones de un punto P perteneciente a una circunferencia O’ o generatriz que rueda sin resbalar sobre otra fija O de radio menor o directriz, siendo ambas tangentes entre sí. Para su trazado, dibujamos ambas circunferencias tangentes en P y dividimos la directriz en cualquier número de partes iguales, 1, 2, 3.. ocho en el ejemplo y trasladamos las longitudes de estas divisiones sobre la generatriz (rectificación inversa) igual número de veces, 1’, 2’, 3’….
Trazamos una circunferencia de radio O-O’ y prolongamos en sentido contrario los radios correspondientes a las divisiones 1, 2, 3.. hasta cortar en A, B, C a esta circunferencia. Con centro en A y radio A1 trazamos un arco que corta en P1, punto de la curva a otro trazado con centro en O y radio O1’. Con centro en B, radio B2 y centro en O y radio O2’ obtenemos P2 y así sucesivamente. Los puntos se unen a mano alzada.
Lemniscata de Bernoulli
Estamos finalizando las curvas técnicas y quiero presentar dentro de las curvas de transición a la lemniscata de Bernoulli (Jacques Bernoulli fue un matemático suizo del siglo XVII. Sólo presentarla (aunque sea de manera un poco diferente), porque es compleja analíticamente, pero el trazado y de dónde viene podemos verlo.
Si seccionamos un toro… aquí he de aclarar bien el significado, pues la gente lo primero que piensa es en el animal y en realidad ¡tiene un gran contenido geométrico!. Un toro es una superficie de revolución engendrada por una circunferencia que gira alrededor de una recta fija de su plano (eje), que no la corta. De forma “familiar” podríamos verlo como un donut.
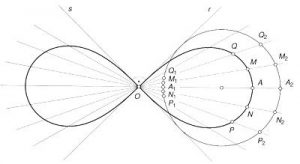
Pues bien, si seccionamos un toro por un plano paralelo a su eje obtendremos óvalos de Cassini, con diferentes formas según el plano esté más cerca o lejos de dicho eje (simplificando mucho la forma de expresarlo). En el dibujo de abajo está la lemniscata de Bernoulli, caso particular de los óvalos de Cassini. Como veis se asemeja al símbolo de infinito: ∞
El trazado es sencillo:
-
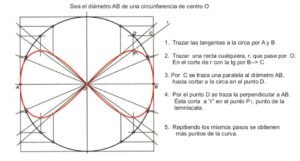
Trazar dos rectas perpendiculares r y s.
-
Trazar una circunferencia tangente a las dos rectas con el radio que queramos
-
Por O (intersección de r y s), trazar rectas secantes a la circunferencia. Cada secante intercepta en una pareja de puntos, como la pareja M 1 y M 2
-
Tomar la longitud de cada cuerda y situar en la recta a partir de O obteniendo puntos exactos de la curva como OM al tomar la cuerda M1-M 2, ON= N1 N2, OP= P1 P 2…
-
Al unir los diferentes puntos M, N, P… la curva queda determinada.
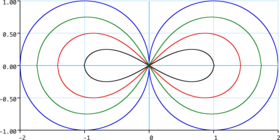
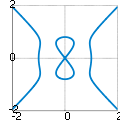
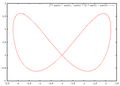
Lemniscata de Gerono
Lemniscata de Gerono: conjunto de soluciones de x4−x2+y2=05
La lemniscata de Gerono o lemniscata de Huygens, es el conjunto de ceros del polinomio cuártico {\displaystyle y^{2}-x^{2}(a^{2}-x^{2})}.67 La curva de Viviani, una curva tridimensional formada por la intersección de una esfera con un cilindro, también tiene una figura de ocho, y toma la forma de la lemniscata de Gerono cuando se proyecta sobre un plano.
Curvas trigonométricas
Son curvas planas y abiertas, representación gráfica de las funciones seno, coseno y tangente.
CONSTRUCCIÓN DE LA SENOIDE O SINUSOIDE. CURVA GRÁFICA DEL SENO.
Dividimos la circunferencia en un número cualquiera de partes iguales y en ese mismo número de partes la rectificación de la circunferencia AB dispuesta en la misma dirección que el radio horizontal. Trazamos perpendiculares al segmento AB por las divisiones obtenidas. Trazamos paralelas al segmento AB por las divisiones de la circunferencia obteniendo puntos de la curva donde se cortan con las normales correspondientes Los puntos así obtenidos se unen ordenadamente a mano alzada o con plantilla de curvas.
Curvas trigonométricas: gráfica del seno, gráfica de la función coseno y gráfica de la función tangente.
CONSTRUCCIÓN DE LA CURVA GRÁFICA DE LA FUNCIÓN COSENO.
En la gráfica del seno, comenzamos a numerar las divisiones a partir del diámetro horizontal. Para trazar la gráfica del coseno se procede de igual forma que en el ejercicio anterior pero comenzando la numeración de las divisiones de la circunferencia a partir del diámetro vertical.
Curvas trigonométricas: gráfica del seno, gráfica de la función coseno y gráfica de la función tangente.
CONSTRUCCIÓN DE LA CURVA GRÁFICA DE LA FUNCIÓN TANGENTE.
Dividimos la circunferencia y numeramos estas divisiones de igual modo que lo hicimos en la gráfica del seno. Rectificamos de igual modo la circunferencia, dividimos el segmento AB y trazamos las perpendicular por estas divisiones. Trazamos rectas tangentes a la circunferencia por los extremos del diámetro horizontal y prolongamos los diámetros que pasan por las divisiones hasta cortar a estas tangentes. Desde estos puntos de corte se trazan paralelas al segmento AB hasta cortar a las normales correspondientes.
El diámetro vertical, paralelo a las rectas tangentes, se corta con ellas en el infinito, la representación gráfica de la función tangente tendrá por tanto los puntos correspondientes a las divisiones 4 y 10 en el infinito pues son puntos asintóticos (asíntota: tangente a la curva en el infinito).
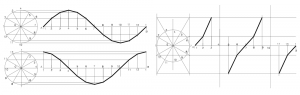Construcción de curvas trigonométricas.
Lemniscata de Booth
La consideración de las curvas con una figura en forma de ocho se remonta a Proclo, un filósofo y matemático griego del neoplatonismo que vivió en el siglo V a. C. Proclo consideró las secciones de un toro por planos paralelos al eje del toro. Como observó, para la mayoría de las secciones, la sección transversal consiste en uno o dos óvalos; sin embargo, cuando el plano es tangente a la superficie interna del toro, la sección transversal toma una figura con forma de ocho, a la que denominó con la palabra griega hipopoda (por su similitud con la atadura utilizada para inmovilizar dos de las patas de un caballo manteniéndolas juntas). El nombre «lemniscata de Booth» para esta curva se remonta a su estudio por parte del matemático del siglo XIX James Booth.1
La lemniscata se puede definir como un curva algebraica, el conjunto de ceros del polinomio cuártico {\displaystyle (x^{2}+y^{2})^{2}-cx^{2}-dy^{2}} cuando el parámetro d es negativo. Para valores positivos de d se obtiene una hipopoda.
Otras curvas
Curva del diablo
Besace
CURVAS CÓNICAS
Consideraciones generales sobre las curvas cónicas
Definición
Se denomina superficie cónica de revolución, a la superficie generada por una recta denominada generatriz, al girar entorno a otra recta denominada eje.
El punto donde la generatriz corta al eje se denomina vértice V de la superficie cónica.
Si un plano α, intercepta a una superficie cónica de revolución, la sección producida se denomina superficie cónica, y su contorno es una curva plana de segundo grado.
Las curvas cónicas propiamente dichas son tres Elipse, Parábola e Hipérbola.
La Elipse se genera cuando el plano α es oblicuo respecto al eje, y corta a todas las generatrices.
La Parábola se genera cuando el plano a es paralelo a una generatriz.
La Hipérbola se genera cuando el plano a es paralelo a dos generatrices. Por cuestiones didácticas y de mejor comprensión, se suele representar utilizando un plano a paralelo al eje de la superficie cónica de revolución.
En la siguiente figuras puedes apreciar mejor en rojo, las curvas cónicas obtenidas.
Al interceptar una superficie cónica de revolución con un plano, podemos contemplar dos ángulos, el a formado por el eje y la generatriz, y el β formado por el eje y el plano de corte.
La relación entre estos ángulos determina el tipo cónica generada, como se puede apreciar en las figuras siguientes.
Cónicas singulares o degeneradas
En función de la posición del plano de corte y las propiedades del cono, se pueden obtener otras curvas cónicas que se denominan singulares o degeneradas.
Teorema de Dandelín
Según el teorema de Dandelín, si trazamos las esferas tangentes interiores a la superficie cónica de revolución y al plano el a que la corta, los puntos de intersección f y f’ de dicha esfera con la recta r, eje de las curvas cónicas, son los denominados focos de las curvas.
Mientras en la elipse y en la hipérbola hay dos focos, en la parábola solo tendremos uno.
La Elipse
Definición
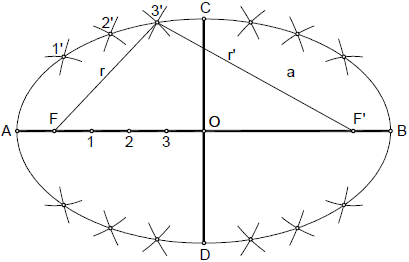
La elipse es una curva cerrada y plana, que se define como el lugar geométrico de los puntos del plano cuya suma de distancias r+r’, a dos puntos fijos F y F’, denominados focos, es constante e igual a 2a, siendo 2a la longitud del eje mayor A-B de la elipse.
La elipse tiene dos eje, el eje mayor A-B, también llamado real, y el eje menor C-D, ambos se cruzan perpendicularmente en el centro O de la elipse.
La longitud del eje mayor es 2a, la del eje menor 2b y la distancia focal 2c, y se cumple que a² = b² + c².
La elipse es simétrica respecto a los dos ejes.
Las rectas que unen un punto cualquiera de la elipse P, con los focos, se denominan radios vectores r y r’, y por definición se cumple que r + r’ = 2a.
Propiedades y elementos
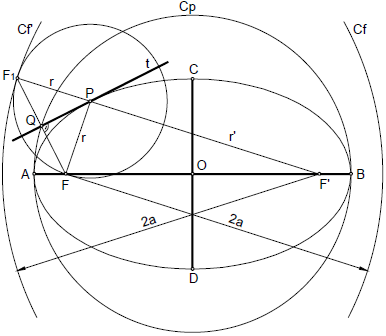
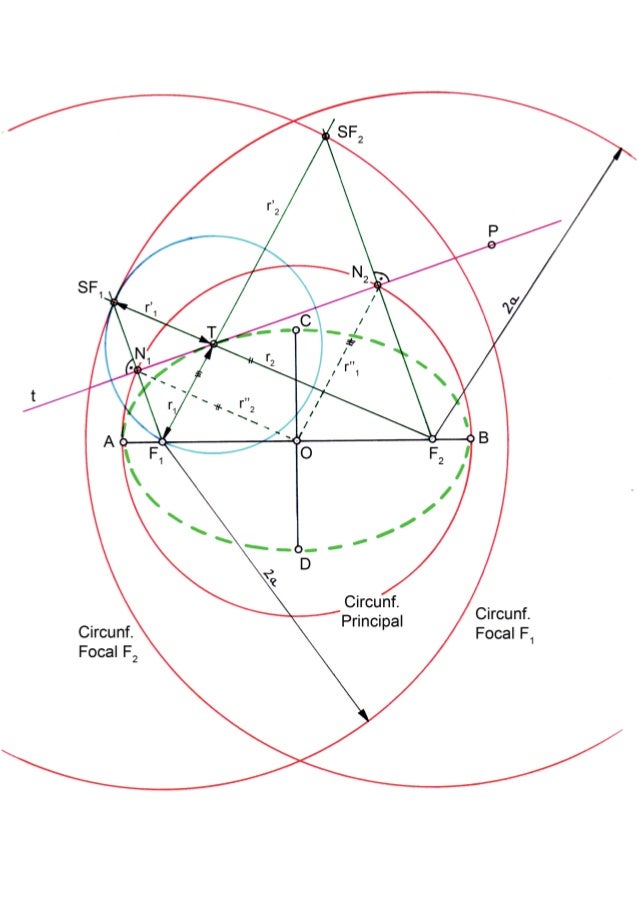
Se denomina circunferencia principal Cp, a la circunferencia de centro O, y diámetro 2a. La circunferencia principal, se define como el lugar geométrico de los pies de las perpendiculares(Q), trazadas desde los focos a las tangentes (t) de la elipse. También se puede definir como el punto medio de los segmentos que unen un foco, con la circunferencia focal del otro foco, y las mediatrices de dichos segmentos, son tangentes a la elipse
Se denomina circunferencia focal Cf, a la circunferencia de centro en uno de los focos de la elipse, y radio 2a. En una elipse se podrán trazar dos circunferencias focales. La circunferencia focal, se define como el lugar geométrico de los puntos simétricos del otro foco (F1), respecto a las tangentes (t) de la elipse.
Observando la figura, también podemos definir la elipse, como el lugar geométrico de los centros de circunferencia que pasan por un foco, y son tangentes a la circunferencia focal del otro foco.
Concepto de diámetros conjugados
Si tenemos un diámetro de la elipse A’B’, el diámetro conjugado con él, es el lugar geométrico de los centros de las cuerdas paralelas a dicho diámetro (1, 2, 3, 4, etc.), estos centros determinan el diámetro conjugado D’C’ del dado.
Los ejes reales de la elipse, son los únicos diámetros conjugados perpendiculares entre si.
Mediante dos diámetros conjugados, podremos construir la elipse directamente, o bien obtener los ejes reales de la misma.
Obtención de los ejes reales, a partir de dos ejes conjugados
Dados los ejes conjugados de una elipse A’B’ y C’D’, podremos obtener a partir de ellos los ejes reales de la elipse, para ello seguiremos los siguientes pasos:
1.- Por O, centro de la elipse, trazaremos la perpendicular al eje conjugado A’B’, y sobre el llevaremos la distancia O-A’, determinando el punto 1.
2.- Uniremos el punto 1 con C’, y determinaremos el punto medio 2, de dicho segmento.
3.- Con centro en 2, trazaremos un arco de radio 2-O, que determinará sobre la prolongación del segmento 1-C’, los puntos 3 y 4. Las rectas O-3 y O-4 determinan las direcciones perpendiculares de los ejes reales de la elipse.
4.- Con centro en 2 trazaremos la circunferencia de diámetro 1-C’. Uniendo el centro O con 2, determinaremos sobre dicha circunferencia, los puntos 5 y 6, siendo las distancias O-5 y O-6, las dimensiones de los semiejes reales de la elipse.
5.- Solo resta llevar, mediante los correspondientes arcos de circunferencias, las dimensiones anteriores sobre las direcciones de los ejes, obteniendo así los ejes reales de la elipse AB y CD
.
Trazado de la elipse mediante radios vectores
Teniendo en cuenta la definición de la elipse, como el lugar geométrico de los puntos del plano, cuya suma de distancias a los focos es igual a 2a, longitud del eje mayor de la elipse, solo necesitaremos coger pares de radios vectores, cuya suma sea 2a, para ello determinaremos una serie de puntos sobre el eje mayor 1, 2, 3 etc., y cogeremos como parejas de radios vectores, los segmentos A1-B1, A2-B2, A3-B3, y así sucesivamente, determinando los puntos 1′, 2′, 3′, etc. de la elipse.
Con cada pareja de radios vectores, se determinarán cuatro puntos de la elipse, uno en cada cuadrante de la misma.
Cuanto mayor sea el número de puntos, mayor será la precisión del trazado de la elipse, que deberá realizarse, o bien a mano alzada o mediante reglas flexibles, o plantillas de curvas especiales.
Trazado de la elipse por haces proyectivos
Trazaremos el rectángulo AOCE, y dividiremos los lados AO y AE en un mismo número de partes iguales.
Seguidamente iremos trazando las rectas C1-D1, C2-D2, etc. y en sus intersecciones iremos obteniendo puntos de la elipse. Esto se repetirá para los cuatro cuadrantes de la elipse.
Trazado de la elipse por haces proyectivos, dados dos ejes conjugados
Trazaremos el romboide A’O’C’E’, y dividiremos los lados A’O’ y A’E’ en un mismo número de partes iguales.
Seguidamente iremos trazando las rectas C’1-D’1, C’2-D’2, etc. y en sus intersecciones iremos obteniendo puntos de la elipse. Esto se repetirá para los cuatro cuadrantes de la elipse.
Trazado de la elipse por envolventes
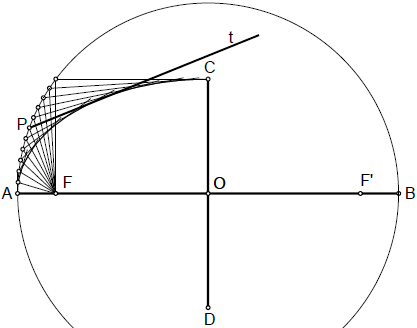
Esta construcción se basa en el hecho de que la circunferencia principal de una elipse, es el lugar geométrico de los pies de las perpendiculares trazadas desde los focos a las tangentes a la elipse.
Para este trazado partiremos de puntos de la circunferencia principal, como el P, indicado en la figura. Uniremos dicho punto con el foco F, y trazaremos por P la perpendicular al segmento PF, obteniendo la recta t, tangente a la elipse. Repitiendo esta operación, obtendremos una serie de tangentes que irán envolviendo a la elipse.
Trazado de la elipse a partir de circunferencias afines
Comenzaremos trazando las circunferencias de centro O, y diámetros AB y CD.
Seguidamente trazaremos radios como el O1, que corta a las circunferencias anteriores en los puntos 1 y 2. Por dichos puntos trazaremos las paralelas a CD y AB respectivamente. Dichas paralelas se cortan en el punto 3, que es de la elipse. El número de radios trazados, serán los necesarios para definir suficientemente la elipse.
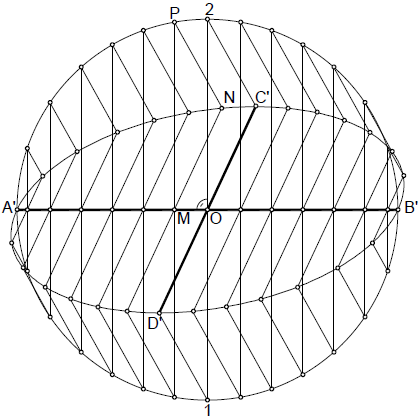
Trazado de la elipse a partir de dos diámetros conjugados por triángulos semejantes afines
Partiendo de los ejes conjugados A’B’ y C’D’, comenzaremos trazando la circunferencia de centro O y diámetro A’B’.
Sobre la circunferencia anterior, trazaremos cuerdas perpendiculares a A’B’, como la 1-2. Uniendo 2 con C’, y 1 con D’, obtendremos los triángulos O2C‘ y O1D’. Solo restará construir en el resto de cuerdas triángulos semejantes a estos como el MPN, de lados paralelos al triángulo O2C’, obteniendo así puntosde la elipse
.
Recta tangente y normal en un punto de la elipse
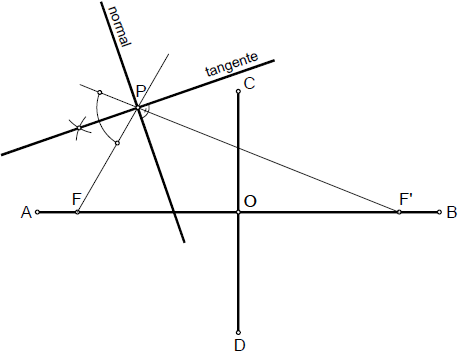
La tangente a la elipse en un punto de ella P, es la bisectriz del ángulo exterior que forman los radios vectores en dicho punto.
La normal en P, es la perpendicular a la tangente en dicho punto.
Recta tangente a la elipse en un punto, por circunferencia principal
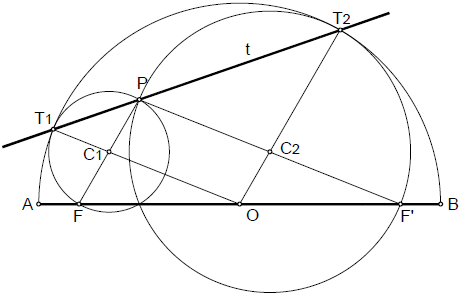
Siendo P el punto de la elipse, comenzaremos trazando las circunferencias de centro C1 y C2, puntos medios de los radios vectores del punto P, y diámetro dichos radios vectores.
Las circunferencias anteriores resultan ser tangentes interiores a la circunferencia principal, en los puntos T1 y T2, determinados al unir el centro O de la elipse con los centros C1 y C2.
Se cumple que los puntos T1, P y T2, están alineados, y determinan la recta t tangente a la elipse buscada.
También se verifica que las rectas F-P y O-T2, y F’-P y O-T1 son respectivamente paralelas.
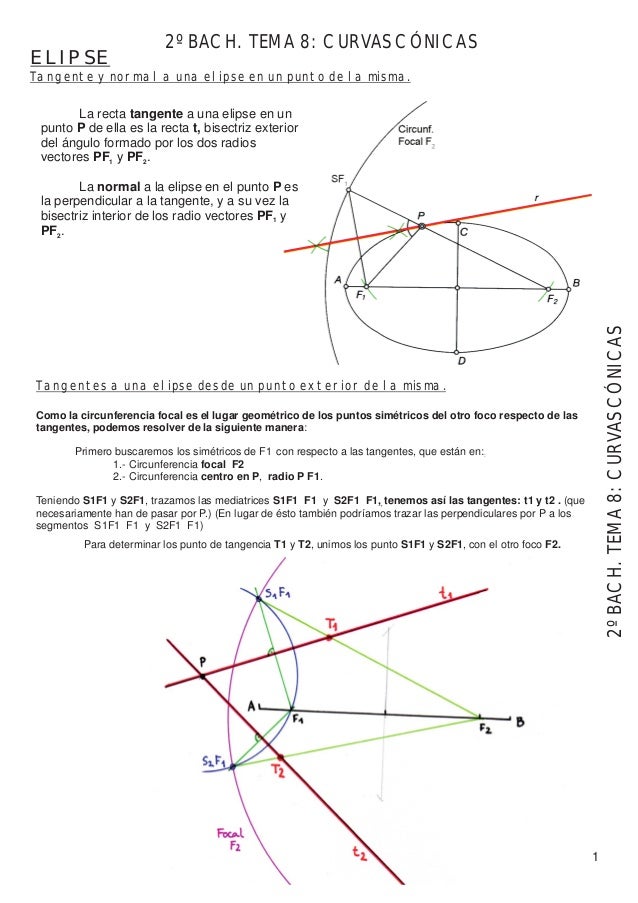
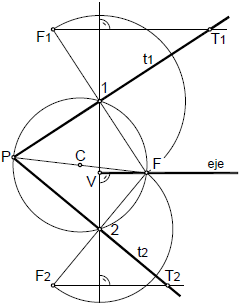
Rectas tangentes a la elipse desde un punto exterior, por circunferencia focal
Esta construcción se basa en la definición de circunferencia focal, como el lugar geométrico de los puntos simétricos del otro foco, respecto a las tangentes a la elipse.
Dado el punto P exterior a la elipse, comenzaremos trazando la circunferencia focal de centro en F, y a continuación la circunferencia de centro en P, y radio P-F’, la cual corta a la focal en los puntos F’1 y F’2. Dichos puntos son los simétricos del F’ respecto a las tangentes a la elipse desde el punto P.
Solo resta trazar las mediatrices de los segmentos F’-F’1 y F’-F’2, obteniendo así las rectas t1 y t2 que serán las tangentes a la elipse buscadas.
Para determinar los puntos de tangencia, trazaremos las rectas F-F’1 y F-F’2, que determinarán sobre las tangentes t1 y t2, los puntos T1 y T2, puntos de tangencia buscados.
Rectas tangentes a la elipse desde un punto exterior, por circunferencia principal
Dado el punto P exterior a la elipse, comenzaremos trazando la circunferencia principal, y a continuación la circunferencia de centro en C, y diámetro P-F. Ambas circunferencias se interceptan en los puntos 1 y 2.
Las rectas P-1 y P-2, serán las tangentes t1 y t2 buscadas. Para determinar los puntos de tangencia, trazaremos las rectas O1 y O2, y por F’ las correspondientes paralelas, que determinarán sobre las tangentes, los puntos T1 y T2, puntos de tangencia buscados.
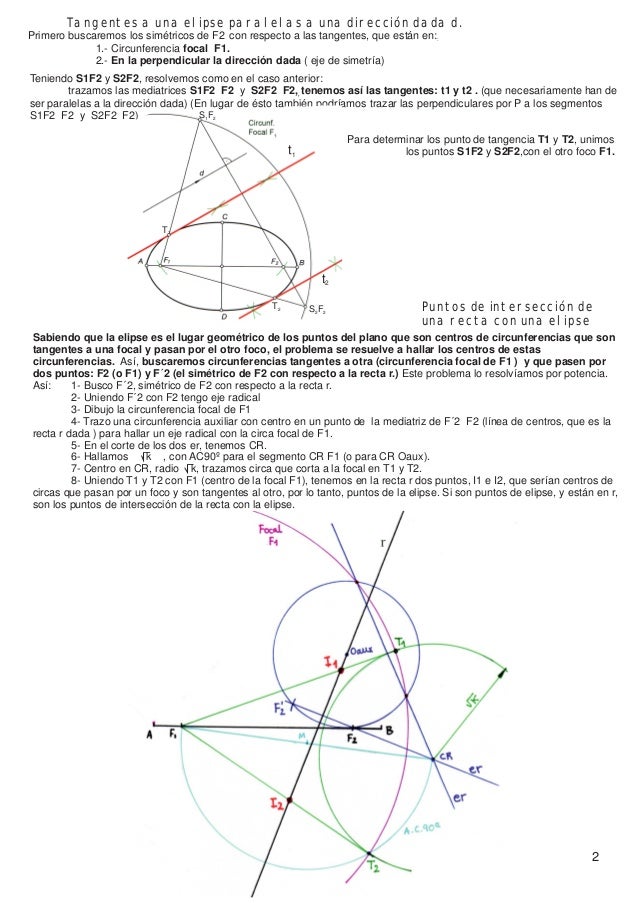
Rectas tangentes a la elipse, paralelas a una dirección dada, por circunferencia focal
Esta construcción es similar a la del trazado de tangentes desde un punto exterior, solo que en este caso el punto es un punto impropio situado en el infinito.
Dada la dirección d, comenzaremos trazando la circunferencia focal de centro en F, y a continuación la recta perpendicular a la dirección d, y que pase por el foco F’. Dicha recta determina sobre la circunferencia focal, los puntos F’1 y F’2.
Las mediatrices de los segmentos F’-F’1 y F’-F’2, serán las tangentes a la elipse t1 y t2 buscadas.
Para determinar los puntos de tangencia, trazaremos las rectas F-F’1 y F-F’2, que determinarán sobre las tangentes t1 y t2, los puntos T1 y T2, puntos de tangencia buscados.
Rectas tangentes a la elipse, paralelas a una dirección dada, por circunferencia principal
Dada la dirección d, comenzaremos trazando la circunferencia principal, y seguidamente la recta perpendicular a la dirección d, y que pase por el foco F’. Dicha recta intercepta a la circunferencia principal en los puntos R y S, pertenecientes a las tangentes buscadas.
Solo restará trazar por R y S las rectas t1 y t2, paralelas a la dirección dada, siendo estas las tangentes buscadas.
Para determinar los puntos de tangencia, trazaremos las rectas OR y OS, y por el foco F, las correspondientes paralelas. Dichas paralelas determinarán sobre las tangentes los puntos T1 y T2 de tangencia buscados.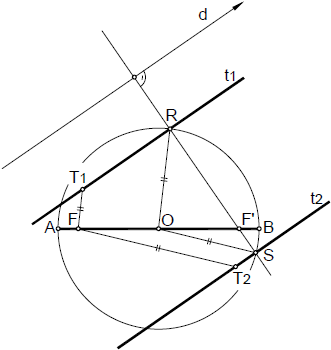
Puntos de intersección de una recta con una elipse
Esta construcción se basa en la definición de la elipse, como el lugar geométrico de los centros de circunferencias que pasan por un foco, y son tangentes a la circunferencia focal del otro foco.
Comenzaremos trazando la circunferencia focal de centro en F y radio 2a. seguidamente trazaremos una circunferencia cualquiera con centro en la recta r, y que pase por el foco F’. En nuestro caso hemos trazado la circunferencia de centro C1. sobre dicha circunferencia determinaremos el punto P, simétrico del foco F’, respecto a la recta r.
Los puntos de intersección buscados, serán los centros de las circunferencias situados en la recta r, que pasando por P y F’, sean tangentes a la circunferencia focal. Por lo tanto el problema se reduce al trazado de circunferencias que pasando por dos puntos sean tangentes a otra dada, Lo que resolveremos por potencia.
En la intersección de las rectas 1-2 y P-F’, obtendremos el punto Cr, centro radical de todas las circunferencias de centro en r y que pasen por P y F’.
Tranzando la circunferencia de diámetro F-Cr y centro en pm, determinaremos en la circunferencia focal, los puntos T1 y T2, puntos de tangencia de las circunferencias buscadas. Determinaremos el centro de dichas circunferencias, uniendo los puntos T1 y T2 con el foco F, rectas que determinarán sobre la recta r dada, los puntos I1 y I2, centro de las circunferencias solución, y por tanto, puntos de intersección de la recta r con la elipse.
Construcción de la elipse por arcos de circunferencias. Radios de curvatura
Para determinar el centro de curvatura en un punto P de la elipse, trazaremos la normal en dicho punto, bisectriz de los dos radios vectores de dicho punto.
La normal trazada, cortará al eje mayor en el punto 1. Por dicho punto trazaremos la perpendicular a la normal, que determinará sobre la recta P-O, el punto 2. Por dicho punto trazaremos la paralela al eje menor de la elipse, que interceptará a la normal en el punto Cp, centro de curvatura buscado.
Partiendo de la normal, podríamos haber llegado a la misma solución, determinando el punto 3 sobre el eje menor. Por dicho punto trazaremos la perpendicular a la normal, que determinará sobre la recta P-O, el punto 4. Por dicho punto trazaremos la paralela al eje mayor de la elipse, que interceptará a la normal en el punto Cp, centro de curvatura buscado.
Para determinar los centros de curvatura en los extremos de los ejes de la elipse, trazaremos el rectángulo OBMC. Seguidamente trazaremos por M, la perpendicular a la recta C-B, que determinará los puntos CB y Cc, respectivamente sobre el eje mayor y menor de la elipse, y que serán los centros de curvatura buscados.
La Parábola
Definición
La parábola es una curva abierta y plana, que se define como el lugar geométrico de los puntos del plano que equidistan de un punto denominado foco, y una recta denominada directriz, observando la figura, FP = PQ = r.
El eje de la parábola es la recta perpendicular a la directriz, que pasa por el foco F. La distancia FD, del foco a la directriz, se denomina parámetro de la parábola, el punto medio del segmento FD, es el punto V, que se denomina vértice de la parábola.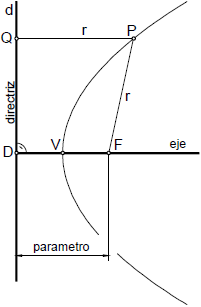
Propiedades y elementos
La parábola se puede considerar como una elipse, uno de cuyos vértices se encuentra en el infinito, así como el centro de la curva. Partiendo de esta consideración, comprobaremos que las propiedades enunciadas para la elipse, se cumplen igualmente en la parábola.
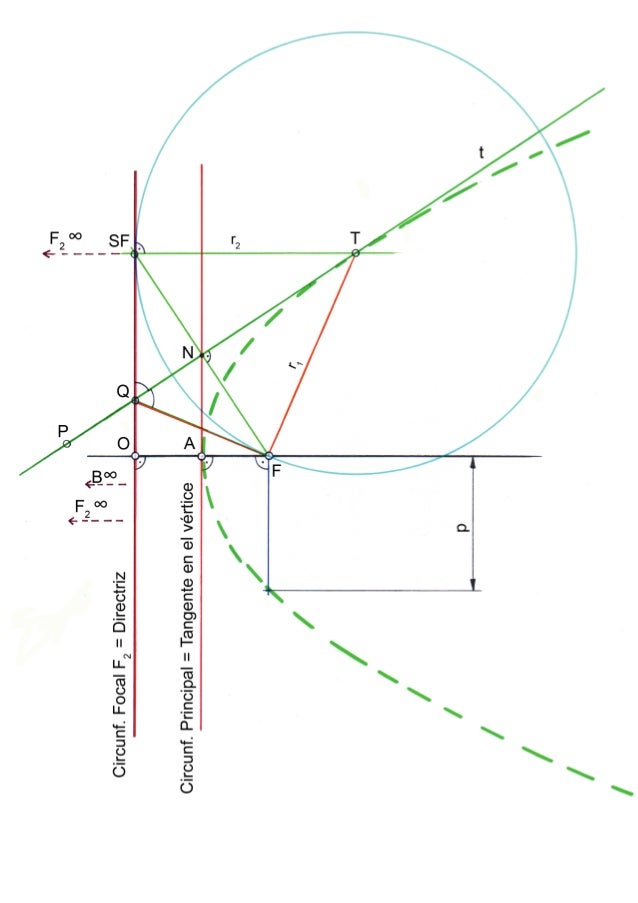
La circunferencia principal Cp, pasará por el vértice V de la curva, y dado que el centro de la curva se encuentra en el infinito, la circunferencia principal resulta ser la recta perpendicular al eje en el vértice V. La circunferencia principal, se define como el lugar geométrico de los pies de las perpendiculares(Q), trazadas desde los focos a las tangentes (t) de la parábola. También se puede definir como el punto medio de los segmentos que unen el foco, con la circunferencia focal del otro foco, y las mediatrices de dichos segmentos, son tangentes a la parábola.
La única circunferencia focal Cf de la parábola, tendrá su centro en el infinito, y deberá pasar por el punto D, simétrico del foco respecto a la tangente el en vértice de la curva, resultando por tanto, una recta coincidente con la directriz de la parábola. La circunferencia focal, se define como el lugar geométrico de los puntos simétricos del foco F, respecto a las tangentes (t) de la parábola.
Observando la figura, también podemos definir la parábola, como el lugar geométrico de los centros de circunferencia que pasan por el foco F, y son tangentes a la circunferencia focal.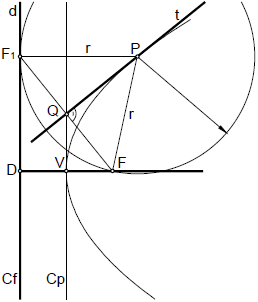
Trazado de la parábola mediante radios vectores
Teniendo en cuanta la definición de la parábola, buscaremos puntos equidistantes del foco F, y la directriz d. Para ello determinaremos una serie de puntos sobre el eje, 1, 2, 3, etc., por los que trazaremos paralelas a la directriz. Trazando arcos de circunferencia de centro en F, y radio las distancias D1, D2, D3, etc., determinaremos sobre las correspondientes paralelas anteriores, los puntos 1′, 2′, 3′, etc., puntos de la parábola buscada.
Con cada pareja de radios vectores, se determinarán dos puntos de la parábola, uno en cada rama de la misma.
Cuanto mayor sea el número de puntos, mayor será la precisión del trazado de la parábola, que deberá realizarse, o bien a mano alzada o mediante reglas flexibles, o plantillas de curvas especiales.
Trazado de la parábola, por haces proyectivos
Comenzaremos obteniendo un punto P de la curva por radios vectores, y trazaremos el rectángulo APCV, y dividiremos los lados AP y PC en un mismo número de partes iguales.
Por las divisiones de AP, trazaremos paralelas al eje de la curva, y uniremos las divisiones de CP, con el vértice V de la curva. La intersección de estas rectas con las paralelas anteriores, determinarán puntos, como el P, pertenecientes a la parábola buscada. Esto se repetirá para la otra rama de la parábola.
Trazado de la parábola, por envolventes
Esta construcción se basa en el hecho de que la circunferencia principal, en este caso, la tangente a la curva en el vértice, es el lugar geométrico de los pies de las perpendiculares trazadas desde el foco a las tangentes a la parábola.
Para este trazado partiremos de puntos 1, 2, 3, etc, de la circunferencia principal. Uniremos dichos puntos con el foco F, y trazaremos por los puntos anteriores perpendiculares a los segmentosl F1, F2, F3, etc., obteniendo las rectas tangentes a la parábola. La curva se determinará mediante tangentes a dichas rectas.
Trazado de la parábola, en base a la definición de la curva
Esta construcción se basa en la definición de la parábola, como el lugar geométrico de los centros de circunferencia que pasan por el foco F, y son tangentes a la circunferencia focal.
Comenzaremos trazando las rectas F1, F2, F3, etc., que unen el foco de la curva F, con puntos de la directriz d.
Seguidamente trazaremos las perpendiculares a los segmentos anteriores, en su punto de intersección con la circunferencia principal, en el caso del segmento F1, en el punto s. Esta perpendicular resulta ser la mediatriz del segmento F1, y tangente a la la curva.
Trazando por el punto 1, una paralela al eje de la curva, dicha paralela interceptará a la tangente anteriormente trazada en el punto T1, punto de la parábola.
Repitiendo con el resto de puntos, obtendremos los suficientes puntos de la curva para poder ser trazada
.
Recta tangente y normal en un punto de la parábola
La tangente a la parábola en un punto de ella P, es la bisectriz del ángulo que forman los radios vectores en dicho punto.
La normal en P, es la perpendicular a la tangente en dicho punto.
Rectas tangentes a la parábola desde un punto exterior, por circunferencia focal
Esta construcción se basa en la definición de circunferencia focal (directriz), como el lugar geométrico de los puntos simétricos del otro foco, respecto a las tangentes a la parábola.
Dado el punto P exterior a la parábola, comenzaremos trazando la circunferencia de centro en P, y radio P–F, la cual corta a la focal (directriz), en los puntos F1 y F2. Dichos puntos son los simétricos del F respecto a las tangentes a la parábola desde el punto P.
Solo resta trazar las mediatrices de los segmentos F–F1 y F–F2, obteniendo así las rectas t1 y t2 que serán las tangentes a la parábola buscadas.
Para determinar los puntos de tangencia, trazaremos las rectas por F1 y F2, rectas paralelas al eje de la curva, que determinarán sobre las tangentes t1 y t2, los puntos T1 y T2, puntos de tangencia buscados.
Rectas tangentes a la parábola desde un punto exterior, por circunferencia principal
Dado el punto P exterior a la parábola, comenzaremos trazando la circunferencia principal (tangente en el vértice), y a continuación la circunferencia de centro en C, y diámetro P–F. Ambas circunferencias se interceptan en los puntos 1 y 2.
Las rectas P–1 y P–2, serán las tangentes t1 y t2 buscadas. Para determinar los puntos de tangencia, haremos 1–F1=1–F y 2–F2=2–F, y por F1 y F2, trazaremos rectas paralelas al eje de la curva, que determinarán sobre las tangentes t1 y t2, los puntos T1 y T2, puntos de tangencia buscados.
Rectas tangentes a la parábola, paralelas a una dirección dada, por circunferencia focal
Esta construcción es similar a la del trazado de tangentes desde un punto exterior, solo que en este caso el punto es un punto impropio situado en el infinito.
Dada la dirección d, comenzaremos trazando la recta perpendicular a la dirección d, y que pase por el foco F. Dicha recta determina sobre la circunferencia focal (directriz), el punto F1.
La mediatriz del segmento F–F1, será la tangente a la parábola t buscada.
Para determinar el punto de tangencia, trazaremos pro F1, la recta paralela al eje de la curva, que determinarán sobre la tangente t, el punto T1, punto de tangencia buscado.
Rectas tangentes a la parábola, paralelas a una dirección dada por circunferencia principal
Dada la dirección d, comenzaremos trazando la circunferencia principal (tangente en el vértice), y seguidamente la recta perpendicular a la dirección d, y que pase por el foco F. Dicha recta intercepta a la circunferencia principal en el punto 1, perteneciente a la tangente buscada.
Solo restará trazar por 1 la recta t, paralela a la dirección dada, siendo esta la tangentes buscada.
Para determinar los puntos de tangencia, haremos 1–F1=1–F, y por F1 trazaremos una recta paralela al eje de la curva, que terminará sobre la tangente t el punto T1, punto de tangencia buscado.
Puntos de intersección de una recta con una parábola
Esta construcción se basa en la definición de la parábola, como el lugar geométrico de los centros de circunferencias que pasan por el foco, y son tangentes a la circunferencia focal del otro foco (directriz).
Comenzaremos trazando una circunferencia cualquiera con centro en la recta r, y que pase por el foco F. En nuestro caso hemos trazado la circunferencia de centro O. Sobre dicha circunferencia determinaremos el punto F1, simétrico del foco F, respecto a la recta r.
Los puntos de intersección buscados, serán los centros de las circunferencias situados en la recta r, que pasando por F1 y F, sean tangentes a la circunferencia focal (directriz). Por lo tanto el problema se reduce al trazado de circunferencias que pasando por dos puntos sean tangentes a una recta dada (directriz), Lo que resolveremos por potencia.
Prolongando la recta F–F1, determinaremos sobre la directriz el punto Cr, centro radical de todas las circunferencias de centro en r y que pasen por F y F1.
Con centro en pm, punto medio del segmento F–Cr, trazaremos la circunferencia de diámetro F–Cr, y por F1 la perpendicular a dicho diámetro, determinando sobre la circunferencia anterior el punto 1.
Con centro en Cr trazaremos el arco de circunferencia de radio Cr–1, que nos determinará sobre la directriz, los puntos T1 y T2. Las perpendiculares a la directriz en dichos puntos, determinarán sobre la recta r los puntos I1 e I2 de intersección de la recta con la parábola.
.
Construcción de la parábola por arcos de circunferencia. Radios de curvatura.
Para determinar el centro de curvatura en un punto P de la parábola, trazaremos la normal en dicho punto, bisectriz de los dos radios vectores de dicho punto.
La normal trazada, cortará al eje en el punto 1. Por dicho punto trazaremos la perpendicular a la normal, que determinará sobre la recta trazada por P y paralela al eje, el punto 2. Por dicho punto trazaremos la perpendicular al eje, que interceptará a la normal en el punto Cp, centro de curvatura buscado.
El centro de curva en el vértice de la curva Cv, lo determinaremos haciendo F–C
La Hipérbola
Definición
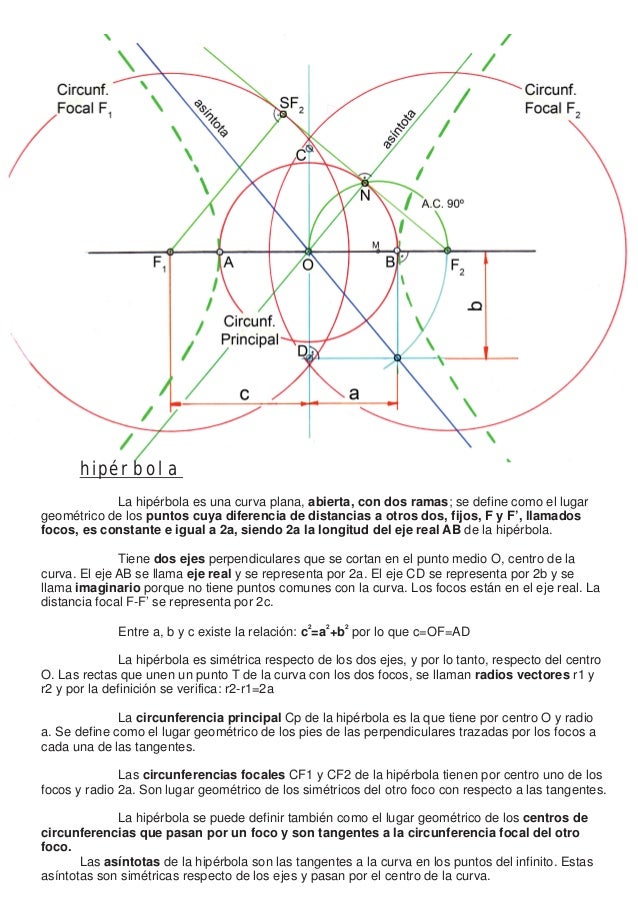
La hipérbola es una curva abierta y plana, con dos ramas, que se definen como el lugar geométrico de los puntos del plano cuya diferencia de distancias r’–r, a dos puntos fijos F y F’, denominados focos, es constante e igual a 2a, siendo 2a la longitud del eje real A–B de la hipérbola. Al eje CD, se le denomina eje imaginario, siendo su longitud 2b. Ambos ejes se cruzan perpendicularmente en el centro O, punto medio de los dos ejes. Por lo tanto, la hipérbola es simétrica, respecto a los dos ejes.
Si, como vemos, la distancia focal F–F’ es igual a 2c, se cumplirá que c² = a² + b².
Las rectas que unen un punto cualquiera de la elipse P, con los focos, se denominan radios vectores r y r’, y por definición se cumple que r’–r = 2a.
Según las dimensiones de los semiejes, se obtendrán tres tipos de parábolas:
- Si a > b, se obtendrá una curva de ramas cerradas.
- Si a = b, se obtendrá una hipérbola equilátera.
- Si a < b, se obtendrá una curva de ramas abiertas.
Propiedades y elementos
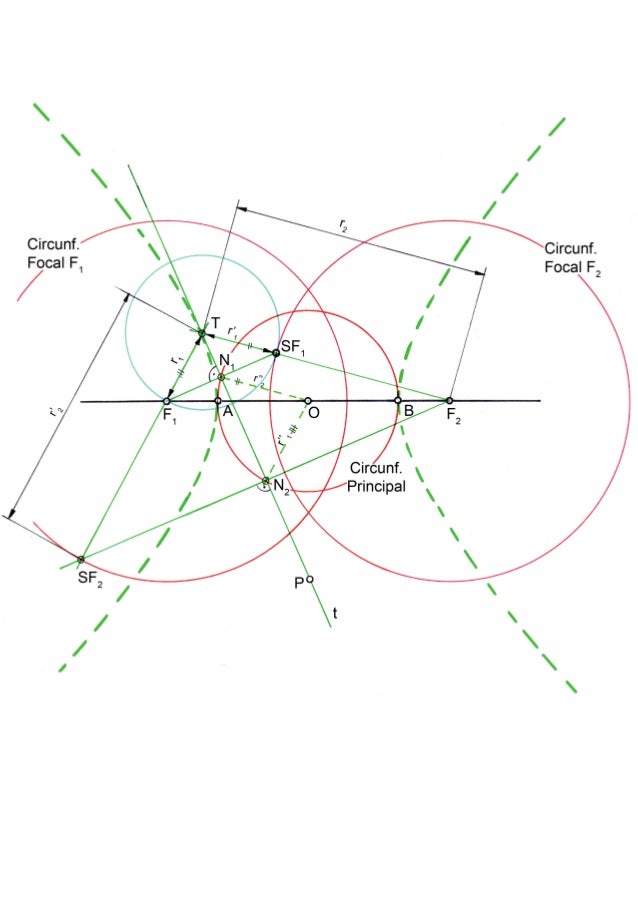
Se denomina circunferencia principal Cp, a la circunferencia de centro O, y diámetro 2a. La circunferencia principal, se define como el lugar geométrico de los pies de las perpendiculares(Q), trazadas desde los focos a las tangentes (t) de la hipérbola. También se puede definir como el punto medio de los segmentos que unen un foco, con la circunferencia focal del otro foco, y las mediatrices de dichos segmentos, son tangentes a la hipérbola.
Se denomina circunferencia focal Cf, a la circunferencia de centro en uno de los focos de la hipérbola, y radio 2a. En una hipérbola se podrán trazar dos circunferencias focales. La circunferencia focal, se define como el lugar geométrico de los puntos simétricos del otro foco (F1), respecto a las tangentes (t) de la hipérbola.
Observando la figura, también podemos definir la hipérbola, como el lugar geométrico de los centros de circunferencia que pasan por un foco, y son tangentes a la circunferencia focal del otro foco.
Trazado de la hipérbola mediante radios vectores
Teniendo en cuenta la definición de la hipérbola, solo necesitaremos coger pares de radios vectores, cuya diferencia sea 2a, para ello determinaremos una serie de puntos sobre el eje real, 1, 2, 3 etc., y cogeremos como parejas de radios vectores, los segmentos A1–B1, A2–B2, A3–B3, y así sucesivamente, determinando los suficientes puntos de la parábola, como para ser definida.
Con cada pareja de radios vectores, se determinarán cuatro puntos de la hipérbola, uno en cada cuadrante de la misma.
Cuanto mayor sea el número de puntos, mayor será la precisión del trazado de la hipérbola, que deberá realizarse, o bien a mano alzada o mediante reglas flexibles, o plantillas de curvas especiales.
Trazado de la hipérbola por haces proyectivos
Comenzaremos obteniendo un punto P de la curva por radios vectores, y trazaremos el rectángulo ARPS, y dividiremos los lados RP y PS en un mismo número de partes iguales. Sobre la prolongación de PR y PS llevaremos esas misma divisiones.
Seguidamente trazaremos rectas que unan el vértice A, con las divisiones de PR, y el vértice Br con las divisiones de PS, obteniendo en sus intersecciones, puntos, pertenecientes a la hipérbola buscada. Esto se repetirá para la otra rama de la hipérbola.
Trazado de la parábola por envolventes
Esta construcción se basa en el hecho de que la circunferencia principal, es el lugar geométrico de los pies de las perpendiculares trazadas desde el foco a las tangentes a la hipérbola.
Para este trazado partiremos de puntos, de la circunferencia principal. Uniremos dichos puntos con el foco F’, y trazaremos por ellos, perpendiculares a las rectas trazadas, obteniendo las rectas tangentes a la parábola. La curva se determinará mediante tangentes a dichas rectas.
Las asíntotas serán las tangentes a la hipérbola en el infinito, y que determinaremos trazando el arco de centro en O y radio O–F. En la intersección de dicho arco con la perpendicular al eje real, trazada por el vértice A, determinaremos el punto 1, perteneciente a la asíntota, solo restará unir dicho punto con el centro O de la hipérbola.
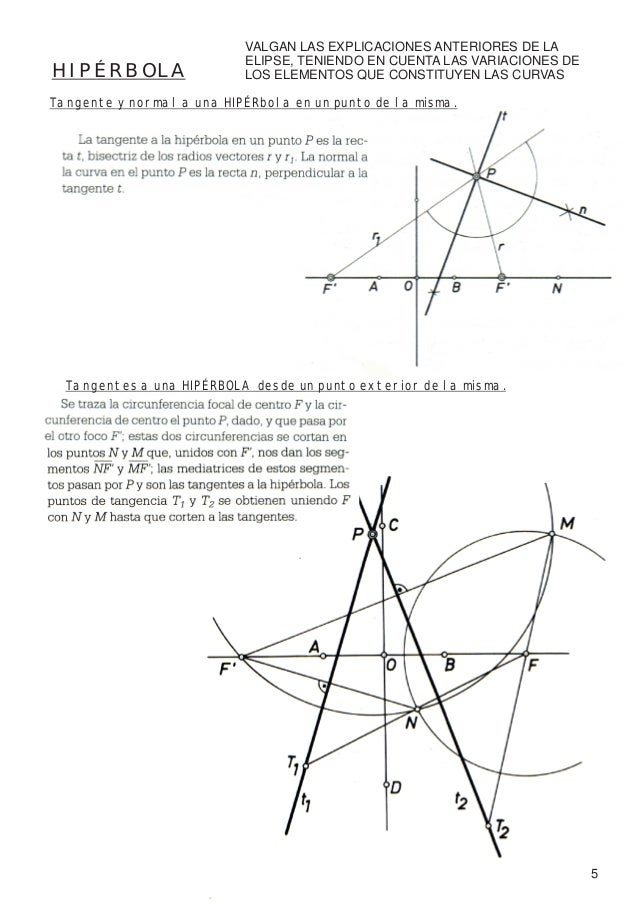
Recta tangente y normal en un punto de la hipérbola
La tangente a la hipérbola en un punto de ella P, es la bisectriz del ángulo que forman los radios vectores en dicho punto.
La normal en P, es la perpendicular a la tangente en dicho punto.
Recta tangente a la hipérbola en un punto, por circunferencia principal
Siendo P el punto de la hipérbola, comenzaremos trazando las circunferencias de centro C1 y C2, puntos medios de los radios vectores del punto P, y diámetro dichos radios vectores.
Las circunferencias anteriores resultan ser tangentes interiores a la circunferencia principal, en los puntos T1 y T2, determinados al unir el centro O de la elipse con los centros C1 y C2.
Se cumple que los puntos T1, T2 y P, están alineados, y determinan la recta t tangente a la hipérbola buscada.
También se verifica que las rectas F–P y O–T2, y F’–P y O–T1 son respectivamente paralelas.
Rectas tangentes a la hipérbola desde un punto exterior, por circunferencia focal
Esta construcción se basa en la definición de circunferencia focal, como el lugar geométrico de los puntos simétricos del otro foco, respecto a las tangentes a la hipérbola.
Dado el punto P exterior a la hipérbola, comenzaremos trazando la circunferencia focal de centro en F’, y a continuación la circunferencia de centro en P, y radio P–F, la cual corta a la focal anterior, en los puntos F1 y F2. Dichos puntos son los simétricos del F respecto a las tangentes a la hipérbola desde el punto P.
Solo resta trazar las mediatrices de los segmentos F–F1 y F–F2, obteniendo así las rectas t1 y t2 que serán las tangentes a la hipérbola buscadas.
Para determinar los puntos de tangencia, trazaremos las rectas F’–F1 y F’–F2, que determinarán sobre las tangentes t1 y t2, los puntos T1 y T2, puntos de tangencia buscados.
Rectas tangentes a la hipérbola desde un punto exterior, por circunferencia principal
Dado el punto P exterior a la hipérbola, comenzaremos trazando la circunferencia principal, y a continuación la circunferencia de centro en C1, y diámetro P–F. Ambas circunferencias se interceptan en los puntos 1 y 2.
Las rectas P–1 y P–2, serán las tangentes t1 y t2 buscadas. Para determinar los puntos de tangencia, trazaremos las rectas O1 y O2, y por F’ las correspondientes paralelas, que determinarán sobre las tangentes, los puntos T1 y T2, puntos de tangencia buscados.
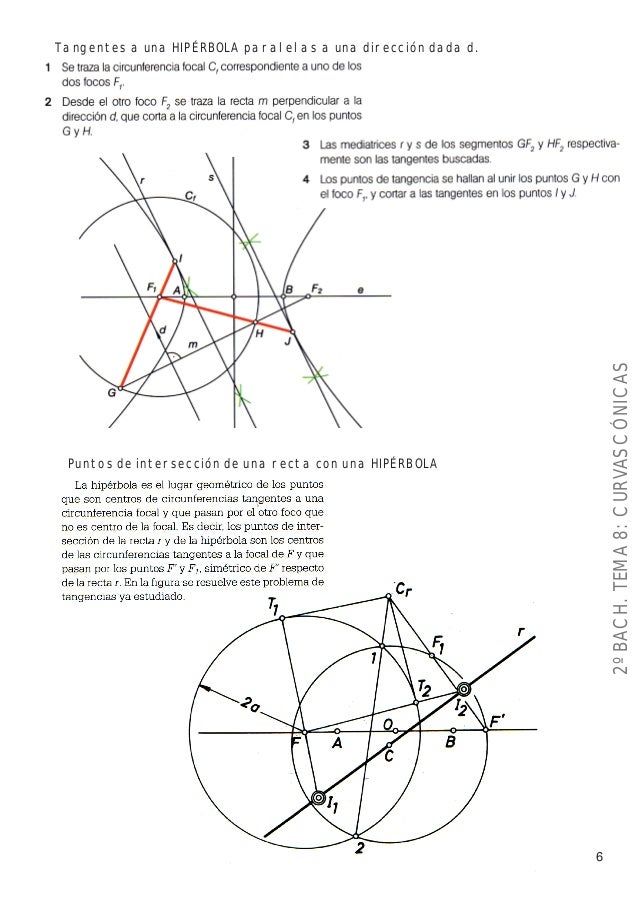
Rectas tangentes a la hipérbola, paralelas a una dirección dada, por circunferencia focal
Esta construcción es similar a la del trazado de tangentes desde un punto exterior, solo que en este caso el punto es un punto impropio situado en el infinito.
Dada la dirección d, comenzaremos trazando la circunferencia focal de centro en F’, y a continuación la recta perpendicular a la dirección d, y que pase por el foco F. Dicha recta determina sobre la circunferencia focal, los puntos F1 y F2.
Las mediatrices de los segmentos F–F1 y F–F2, serán las tangentes a la elipse t1 y t2 buscadas.
Para determinar los puntos de tangencia, trazaremos las rectas F’–F1 y F’–F2, que determinarán sobre las tangentes t1 y t2, los puntos T1 y T2, puntos de tangencia buscados.
Rectas tangentes a la hipérbola, paralelas a una dirección dada, por circunferencia principal
Dada la dirección d, comenzaremos trazando la circunferencia principal, y seguidamente la recta perpendicular a la dirección d, y que pase por el foco F. Dicha recta intercepta a la circunferencia principal en los puntos 1 y 2, pertenecientes a las tangentes buscadas.
Solo restará trazar por 1 y 2 las rectas t1 y t2, paralelas a la dirección dada, siendo estas las tangentes buscadas.
Para determinar los puntos de tangencia, trazaremos las rectas O1 y O2, y por el foco F’, las correspondientes paralelas. Dichas paralelas determinarán sobre las tangentes los puntos T1 y T2 de tangencia buscados.
Puntos de intersección de una recta con una hipérbola
Esta construcción se basa en la definición de la hipérbola, como el lugar geométrico de los centros de circunferencias que pasan por un foco, y son tangentes a la circunferencia focal del otro foco.
Comenzaremos trazando la circunferencia focal de centro en F y radio 2a. seguidamente trazaremos una circunferencia cualquiera con centro en la recta r, y que pase por el foco F’. En nuestro caso hemos trazado la circunferencia de centro C1. sobre dicha circunferencia determinaremos el punto P, simétrico del foco F’, respecto a la recta r.
Los puntos de intersección buscados, serán los centros de las circunferencias situados en la recta r, que pasando por P y F’, sean tangentes a la circunferencia focal. Por lo tanto el problema se reduce al trazado de circunferencias que pasando por dos puntos sean tangentes a otra dada, Lo que resolveremos por potencia.
En la intersección de las rectas 1–2 y P–F’, obtendremos el punto Cr, centro radical de todas las circunferencias de centro en r y que pasen por P y F’.
Tranzando la circunferencia de diámetro F–Cr y centro en pm, determinaremos en la circunferencia focal, los puntos T1 y T2, puntos de tangencia de las circunferencias buscadas. Determinaremos el centro de dichas circunferencias, uniendo los puntos T1 y T2 con el foco F, rectas que determinarán sobre la recta r dada, los puntos I1 y I2, centro de las circunferencias solución, y por tanto, puntos de intersección de la recta r con la hipérbola.
Construcción de la hipérbola por arcos de circunferencia. Radios de curvatura
Para determinar el centro de curvatura en un punto P de la hipérbola, trazaremos la normal en dicho punto, bisectriz del ángulo exterior que forman los dos radios vectores de dicho punto.
La normal trazada, cortará a la prolongación del eje real en el punto 1. Por dicho punto trazaremos la perpendicular a la normal, que determinará sobre la recta O–P, el punto 2. Por dicho punto trazaremos la paralela al eje imaginario de la hipérbola, que interceptará a la normal en el punto Cp, centro de curvatura buscado.
Para determinar los centros de curvatura en los extremos del eje real de la hipérbola, trazaremos la perpendicular a la asíntota en el punto R. Dicha perpendicular interceptará a la prolongación del eje real en el punto CB, centro de curvatura buscado.
GEOMETRÍA PLANA 00 curvas técnicas ciclicas
GEOMETRÍA PLANA 00 curvas cónicas
SISTEMA DIÉDRICO ORTOGONAL
SISTEMA DIÉDRICO ORTOGONAL 02 métodos
SISTEMA DIÉDRICO ORTOGONAL 03 superficies secciones desarrollos
SISTEMA DIÉDRICO ORTOGONAL 04 poliedros regulares desarrollos
SISTEMA AXONOMÉTRICO 05 de pieza a vistas
SISTEMA AXONOMÉTRICO 06 de vistas a piezas
Introducción
En ocasiones, debido a la complejidad de los detalles internos de una pieza, su representación se hace confusa, con gran número de aristas ocultas, y la limitación de no poder acotar sobre dichas aristas. La solución a este problema son los cortes y secciones, que estudiaremos en este tema.
También en ocasiones, la gran longitud de determinadas piezas, dificultan su representación a escala en un plano, para resolver dicho problema se hará uso de las roturas, artificio que nos permitirá añadir claridad y ahorrar espacio.
Las reglas a seguir para la representación de los cortes, secciones y roturas, se recogen en la norma UNE 1-032-82, «Dibujos técnicos: Principios generales de representación», equivalente a la norma ISO 128-82.
Generalidades sobre cortes y secciones
Un corte es el artificio mediante el cual, en la representación de una pieza, eliminamos parte de la misma, con objeto de clarificar y hacer más sencilla su representación y acotación.
En principio el mecanismo es muy sencillo. Adoptado uno o varios planos de corte, eliminaremos ficticiamente de la pieza, la parte más cercana al observador, como puede verse en las figuras.
Como puede verse en las figuras siguientes, las aristas interiores afectadas por el corte, se representarán con el mismo espesor que las aristas vistas, y la superficie afectada por el corte, se representa con un rayado. A continuación en este tema, veremos como se representa la marcha del corte, las normas para el rayado del mismo, etc..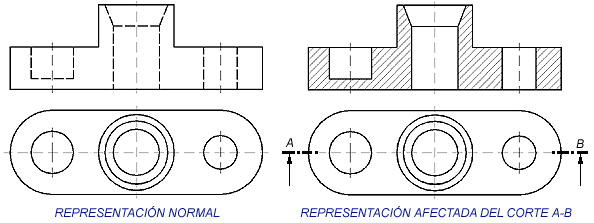
Se denomina sección a la intersección del plano de corte con la pieza (la superficie indicada de color rojo), como puede apreciarse cuando se representa una sección, a diferencia de un corte, no se representa el resto de la pieza que queda detrás de la misma. Siempre que sea posible, se preferirá representar la sección, ya que resulta más clara y sencilla su representación.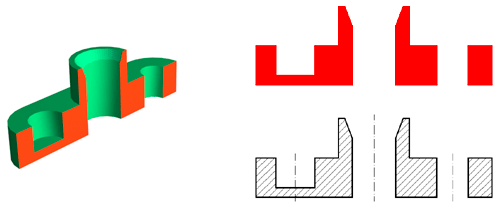
Líneas de rotura en los materiales
Cuando se trata de dibujar objetos largos y uniformes, se suelen representar interrumpidos por líneas de rotura. Las roturas ahorran espacio de representación, al suprimir partes constantes y regulares de las piezas, y limitar la representación, a las partes suficientes para su definición y acotación.
Las roturas, están normalizadas, y su tipos son los siguientes:
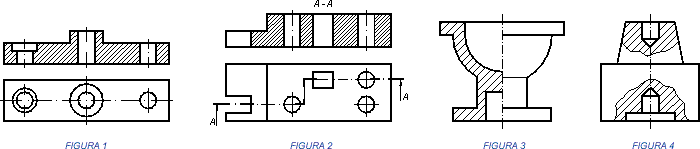
- Las normas UNE definen solo dos tipos de roturas (figuras 1 y 2), la primera se indica mediante una línea fina, como la de los ejes, a mano alzada y ligeramente curvada, la segunda suele utilizarse en trabajos por ordenador.
- En piezas en cuña y piramidales (figuras 3 y 4), se utiliza la misma línea fina y ligeramente curva. En estas piezas debe mantenerse la inclinación de las aristas de la pieza.
- En piezas de madera, la línea de rotura se indicará con una línea en zig-zag (figura 5).
- En piezas cilíndricas macizas, la línea de rotura de indicará mediante las característica lazada (figura 6).
- En piezas cónicas, la línea de rotura se indicará como en el caso anterior, mediante lazadas, si bien estas resultarán de diferente tamaño (figura 7).
- En piezas cilíndricas huecas (tubos), la línea de rotura se indicará mediante una doble lazada, que patentizarán los diámetros interior y exterior (figura 8).
- Cuando las piezas tengan una configuración uniforme, la rotura podrá indicarse con una línea de trazo y punto fina, como la las líneas de los ejes (figura 9).
Representación de la marcha de un corte
Cuando la trayectoria de un corte sea evidente, no será necesaria ninguna indicación (figura 1). En el caso de que dicha trayectoria no sea evidente o se realice mediante varios planos de corte, el recorrido se indicará mediante una línea de trazo y punto fino, que se representará con trazos gruesos en sus extremos y cambios de dirección (figuras 2, 3 y 4).
En los extremos del plano de corte se situarán dos letras mayusculas, que servirán de referencia del mismo, estas letras podrán ser repetidas A-A o consecutivas A-B. También en los extremos se consignan dos flechas, que indican el sentido de observación. Sobre la vista afectada del corte, se indicarán las letras definidoras del corte.
Un corte puede realizarse por diferentes tipos de planos: un único plano (figura 1), por planos paralelos (figura 2), por planos sucesivos (figura 3), y por planos concurrentes (figura 4), en este último caso, uno de ellos se gira antes del abatimiento.
Norma para el rayado de los cortes
Las superficies de una pieza afectadas por un corte, se resaltan mediante un raya de líneas paralelas, cuyo espesor será el más fino de la serie utilizada. Basándonos en las normas UNE, podemos establecer las siguientes reglas, para la realización de los rayado:
- La inclinación del rayado será de 45º respecto a los ejes de simetría o contorno principal de la pieza (figura 1).
- La separación entre las líneas de rayado dependerá de tamaño de la pieza, pero nunca deberá ser inferior a 0,7 mm. ni superior a 3 mm. (figura 2).
- En piezas de gran tamaño, el rayado puede reducirse a una zona que siga el contorno de la superficie a rayar (figura 3).
- En los casos de cortes parciales o mordeduras, la separación entre la parte seccionada y el resto de la pieza, se indica con una línea fina a mano alzada, y que no debe coincidir con ninguna arista ni eje de la pieza (figura 4).
- Las diferentes zonas rayadas de una pieza, pertenecientes a un mismo corte, llevarán la misma inclinación y separación (figura 5), igualmente se mantendrá el mismo rayado cuando se trate de cortes diferentes sobre una misma pieza (figura 6).
- En piezas afectadas por un corte por planos paralelos, se empleará el mismo rayado, pudiendo desplazarse en la línea de separación, para una mayor comprensión del dibujo (figura 7).
- En cortes sobre representaciones de conjuntos, las diferentes piezas se rayarán modificando la inclinación de 45º, y cuando no pueda evitarse, se variará la separación del rayado (figura 8).
- Las superficies delgadas, no se rayan, sino que se ennegrecen. Si hay varias superficies contiguas, se dejará una pequeña separación entre ellas, que no será inferior a 7 mm. (figura 9).
- Debe evitarse la consignación de cotas sobre superficies sobre las superficies rayadas. En caso de consignarse, se interrumpirá el rayado en la zona de la cifra de cota, pero no en las flechas ni líneas de cota (figura 10).
- No se dibujarán aristas ocultas sobre las superficies rayadas de un corte. Y solo se admitirán excepcionalmente, si es inevitable, o con ello se contribuye decisivamente a la lectura e interpretación de la pieza (figura 11).
Elementos que no se seccionan
Las normas establecen como piezas no seccionables: los tornillos, tuercas, arandelas pasadores, remaches, eslabones de cadena, chavetas, tabiques de refuerzo, nervios, orejeras, bolas de cojinetes, mangos de herramientas, ejes, brazos de ruedas y poleas, etc.. A modo de ejemplo se incluyen los ejemplos siguientes: tornillo, tuerca y remache (figura 1), eslabón de cadena (figura 2), mango de herramienta (figura 3), tabiques de refuerzo (figura 4), unión roscada (figura 5), y brazos de polea (figura 6).
Tipos de corte
Los diferentes tipos de cortes que podemos realizar, pueden ser clasificados en tres grandes grupos:
- Corte total, es el producido por uno o varios planos, que atraviesan totalmente la pieza, dejando solamente en vista exterior las aristas de contorno (figuras 1 y 2).
- Semicorte o corte al cuarto (figura 3). Se utilizan en piezas que tienen un eje de simetría, representándose media pieza en sección y la otra mitad en vista exterior. En este tipo de corte nose representarán aristas ocultas, con objeto de que la representación sea más clara. En ocasiones coincide una arista con el eje de simetría, en dicho caso prevalecerá la arista. En este tipo de corte, siempre que sea posible, se acotarán los elementos exteriores de la pieza a un lado, y los interiores al otro.
- Corte parcial o mordedura (figura 4). En ocasiones solo necesitamos poder representar pequeños detalles interiores de una pieza, en estos casos no será necesario un corte total o al cuarto, y será suficiente con este tipo de corte. El corte parcial se delimitará mediante una línea fina y ligeramente sinuosa.
Secciones abatidas
Este tipo de secciones se utilizan siempre que no obstaculicen la claridad de la representación. Están producidas por planos perpendiculares a los de proyección, y se representan girándolas 90º sobre su eje, hasta colocarlas sobre el mismo plano del dibujo. Podremos utilizar los siguientes tipos:
- Secciones abatidas sin desplazamiento. Se representarán delimitadas por una línea fina (figuras 1 y 2).
- Secciones abatidas con desplazamiento. Se representarán delimitadas por una línea gruesa. La sección desplazada puede colocarse en la posición de proyección normal, cerca de la pieza y unida a esta mediante una línea fina de trazo y punto (figura 3), o bien desplazada a una posición cualquiera, en este caso se indicará el plano de corte y el nombre de la sección (figura 4).
- Secciones abatidas sucesivas. El desplazamiento de la sección se podrá realizar a lo largo del eje (figura 5); desplazadas a lo largo del plano de corte (figura 6), o desplazadas a una posición cualquiera (figura 7).
Actividades de repaso y ampliación:
ACTIVIDADES SM 2badt_sv_es_ft fichas trabajo
Actividades de profundización:
01 2bach_triangulos (1) 02 2bach_cuadrilateros (1) 2bach_cuadrilateros 2bach_trazadosgeometricos_paraperpcirc 2bach_triangulos 03 2bach_proporcionalidad-1 04 2bach_equivalencia 05 2bach_arcocapaz1-1 05 2bach_arcocapaz2 06 2bach_transformaciones1 06 6a_2bach_traslacion 06 6b_2bach_giros 06 6c_2bach_simetria 06 25_2bach_homologiainiciacion 06 26_2bach_homologia1 06 27_2bach_afinidadiniciacion 06 28_2bach_afinidad1-1 07 2bach_homotecia 08 8_2bach_tangencias1 08 9_2bach_tangencias2 08 10_2bach_tangenciaslugares 08 11_2bach_tangenciasdilatacion-1 08 13_2bach_tangenciaspotencia1 08 14_2bach_tangenciaspotencia2-1 08 15_2bach_tangenciaspotencia3 09 16_2bach_elipse 09 17_2bach_elipse_conjugados 09 18_2bach_elipse_tangencias 09 19_2bach_elipseinterseccion 09 20_2bach_parabola 09 21_2bach_parabolatangencias 09 22_2bach_parabolainterseccion-1
