Buscando el máximo común divisor
Un problema para todas las generaciones.
octubre 2020
Suma y producto de dos cifras
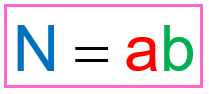
¿Cuántos números de dos cifras verifican que dicho número coincide con la suma de sus cifras más el producto de ellas?
Números simpáticos
Un número es simpático si se puede expresar a la vez como suma de dos números consecutivos y como suma de tres números consecutivos. Por ejemplo, el 45 es un número simpático.
¿Cuántos números simpáticos hay de dos cifras? ¿Cuántos números simpáticos hay de tres cifras?
Curva de Agnesi
Esta curva fue construida por la matemática italiana Maria Gaetana Agnesi (1718-1799). Es el lugar geométrico del punto del plano Q, construido de la siguiente forma:
• Se traza una circunferencia de diámetro a con centro el punto A:(a/2).
• Se traza la tangente a la circunferencia por el punto B:(0,a), que tiene como ecuación y=a.
• Se escoge un punto P cualquiera de la circunferencia.
• La semirrecta con origen el punto O que pasa por P corta a la tangente anterior en el punto C.
• Por el punto P se traza una paralela al eje de abscisas y por el punto C una paralela al eje de ordenadas.
• Estas dos rectas se cortan en un punto Q.
• Al mover el punto P por la circunferencia el punto Q describe la curva de Agnesi.
Haz «click» sobre la imagen para abrir la construcción de Geogebra.
Reptiles
M.C. Escher. Reptiles. 1943.
Litografía, 38’5 × 33’4 cm.
Números pentagonales
Un número pentagonal es un número que se obtiene al sumar los puntos necesarios para construir la sucesión de pentágonos de la figura.
Los primeros números pentagonales son: 1 , 5 , 12 , 22 , 35 , 51, 70 , 92 , 117 , 145 , …
Utilizando la suma de los elementos de una progresión aritmética, se obtiene la fórmula para calcular los números pentagonales.
Múltiplo de 24
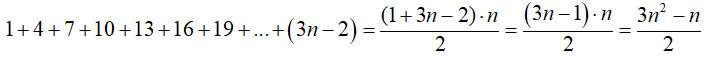
Demostrar que al multiplicar cuatro números naturales consecutivos se obtiene un múltiplo de 24.
Área de la cruz
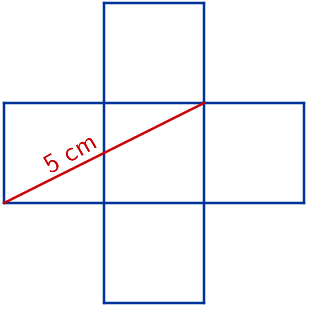
La cruz de la figura está formada por cinco cuadrados iguales. Calcula su área sabiendo que la longitud del segmento rojo es 5 cm.
Circunferencia de los nueve puntos
La circunferencia de los nueve puntos es una circunferencia que tiene por centro el punto medio del segmento que une el ortocentro y el circuncentro y que pasa por:
• Los puntos medios de los tres lados.
• Los pies de las tres alturas (puntos de intersección de las alturas con los lados).
• Los puntos medios de los segmentos que unen el ortocentro y los tres vértices.
Haz «click» sobre la imagen para abrir la construcción con Geogebra y seguirla paso a paso.
Recta de Euler
En cualquier triángulo, el circuncentro, el ortocentro y el baricentro están alineados. La recta que pasa por ellos recibe el nombre de recta de Euler.
Haz «click» sobre la imagen para abrir la construcción con Geogebra y seguirla paso a paso.
Mueve los vértices del triángulo y responde a las siguientes preguntas:
¿Hay algún tipo de triángulo en el que el incentro también pertenezca a la recta de Euler?
¿Hay algún tipo de triángulo en el que no se pueda trazar la recta de Euler?
