La cisoide de Diocles (240 a.C. – 180 a.C.) es una curva algebraica generada de la siguiente forma:
• Se traza una circunferencia y se representa un diámetro, OP.
• Por uno de los extremos del diámetro, P, se traza la tangente a la circunferencia y se escoge un punto, T, de dicha tangente.
• Se traza la semirrecta con origen en el otro extremo del diámetro, O, que pasa por el punto P.
• Se traza una circunferencia con centro en O y radio PT.
• La intersección de esta circunferencia con la semirrecta es el punto Q, que verifica d(O,Q)=d(P,T).
• Al desplazar el punto T por la tangente, el punto Q describe la cisoide.
Haz «click» sobre la imagen para abrir la construcción de GeoGebra.
Construcción, con regla y compás, de un heptágono regular conociendo la longitud del lado.
Haz «click» sobre la imagen para abrir la construcción con GeoGebra y seguirla paso a paso.
Construcción, con regla y compás, de un heptágono regular inscrito en una circunferencia.
Haz «click» sobre la imagen para abrir la construcción con GeoGebra y seguirla paso a paso.
El juego consiste en tres varillas y un número de discos colocados en una de las varillas de mayor a menor tamaño. Hay que pasar la torre de discos de la varilla izquierda a la derecha ayudándose de la varilla central. Las reglas para los movimientos son las siguientes:
• En cada movimiento solo se puede desplazar el disco que haya arriba en alguna de las varillas.
• No se puede colocar un disco sobre uno de menor tamaño en ninguna de las varillas.
El mínimo número de movimientos es 2n–1, siendo n el número de discos.
(Haciendo «click» sobre la imagen puedes practicar con el juego realizado en GeoGebra).
Este puzle fue creado por el ajedrecista Sam Loyd. Construye el tablero de ajedrez con las ocho piezas.
• Para desplazarlas se utiliza el punto de color negro que hay en cada una. (Una vez seleccionada una pieza, se puede desplazar con mayor precisión utilizando las flechas de dirección).
• Para girarlas se utiliza el punto de color blanco que tiene cada pieza en un vértice.
(Haciendo «click» sobre la imagen puedes practicar con el puzle realizado en GeoGebra).
La media aritmética como solución al sobrepeso.
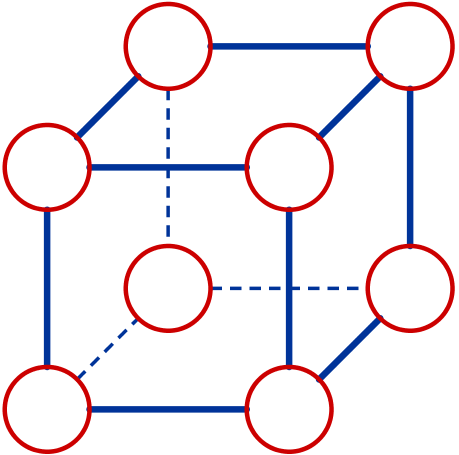
Coloca los números 1, 2, 3, 4, 5, 6, 7 y 8 en los vértices del cubo para que la suma de los números que se encuentran en los vértices de cada una de las caras coincida.
Historias de Pi.
La serie “Universo matemático” fue creada por el profesor Antonio Pérez Sanz y producida por RTVE en 2000. Ahora RTVE la pone a disposición de los docentes a través de su menú “a la carta”.
Haz click sobre la imagen inferior para verlo.
