Construcción de un decágono regular inscrito en una circunferencia
Construcción, con regla y compás, de un decágono regular inscrito en una circunferencia.
Haz «click» sobre la imagen para abrir la construcción con GeoGebra y seguirla paso a paso.
enero 2021
Sophie Germain
Sophie Germain en una carta a C. F. Gauss. «M. Pernety me informó que él le ha comunicado mi nombre. Esto me lleva a confesarle que no soy tan completamente desconocida para usted, como podría creer, pero que por temor a la burla ligada a una mujer científica, he adoptado previamente el nombre de M. Le Blanc en la comunicación de aquellas notas que, sin duda, no merecen la indulgencia con la que me ha correspondido».
Marie Sophie Germain.
París, 1 de abril de 1776 – París, 27 de junio de 1831.
Matemática, física y filósofa francesa.
Hizo contribuciones importantes a la Teoría de Números. Trabajó en la demostración del Teorema de Fermat (por entonces, conjetura), utilizando los números primos de Sophie Germain (un número primo, n, es un número primo de Sophie Germain si 2n+1 también es primo).
Canguro
Juego para dos jugadores. El juego consiste en colocar las piezas en la posición del otro jugador. Gana el primer jugador que lo consiga.
En su turno, cada jugador puede mover una sola ficha, desplazándola una sola casilla en cualquier dirección o realizando todos los saltos que sea posible a cualquier ficha, propia o del otro jugador, en cualquier dirección, siempre que la casilla siguiente no esté ocupada por ninguna ficha.
(Haciendo «click» sobre la imagen puedes practicar con el juego realizado en GeoGebra).
Y una partición más del cuadrado
¿Dónde deben estar situados los puntos A, B, C y D para que las tres regiones en las que se divide el cuadrado tengan la misma superficie?
Otra partición del cuadrado
¿Dónde deben estar situados los puntos A, B y C para que las tres regiones en las que se divide el cuadrado tengan la misma superficie?
Partición de un cuadrado
¿Dónde deben estar situados los puntos P y Q para que las tres regiones en las que se divide el cuadrado tengan la misma superficie?
Estrella hexagonal
Coloca los números 1, 2, 3, 4, 5, 6 y 7 en los círculos para que la suma de los tres círculos situados en cada triángulo equilátero y los círculos situados en las líneas de tres sea la misma.
(Haciendo «click» sobre la imagen puedes practicar con el juego realizado en GeoGebra).
Aproximación gráfica de π de Zu Chongzhi
El número π es un número trascendente, esto significa que no se puede representar con regla y compás. Sin embargo, algunos matemáticos han intentado conseguir alguna aproximación gráfica. El matemático chino Zu Chongzhi (429-500), obtiene la aproximación más precisa durante los 900 años posteriores.
Haz «click» sobre la imagen para abrir la construcción con GeoGebra y seguirla paso a paso.
Demostración de la aproximación gráfica de π de Zu Chongzhi
Aplicando el Teorema de Pitágoras:
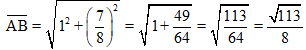
Los triángulos AOB y CDB son semejantes, por tanto:
Los triángulos ADB y CEB son semejantes, por tanto:
Si se añade este segmento a un segmento de longitud tres, tendríamos un segmento de longitud π:
Universo matemático. Capítulo 5.
Gauss: de lo real a lo imaginario.
La serie “Universo matemático” fue creada por el profesor Antonio Pérez Sanz y producida por RTVE en 2000. Ahora RTVE la pone a disposición de los docentes a través de su menú “a la carta”.
Haz click sobre la imagen inferior para verlo.
