Adicción Matemática

febrero 2021

Números impares

Potencias de exponente 7 de los números naturales

Se colocan ahora todos los números impares seguidos según la distribución indicada a continuación. Se completan cubos de arista n y, a continuación, se completan tres pirámides de base cuadrada. En este apartado se estudiará únicamente la suma de los números impares situados en los cubos. De la misma forma que sucedía en las potencias de exponente 5, se puede estudiar la suma de los impares situados en las pirámides, pero el estudio realizado en este artículo se centra en el resultado de los primeros.

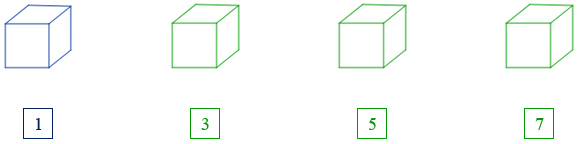
1 = 17

 

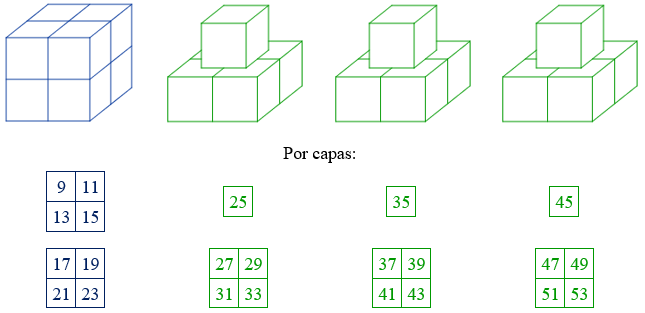
9 + 11 + 13 + 15 + 17 + 19 + 21 + 23 = 128 = 27

 

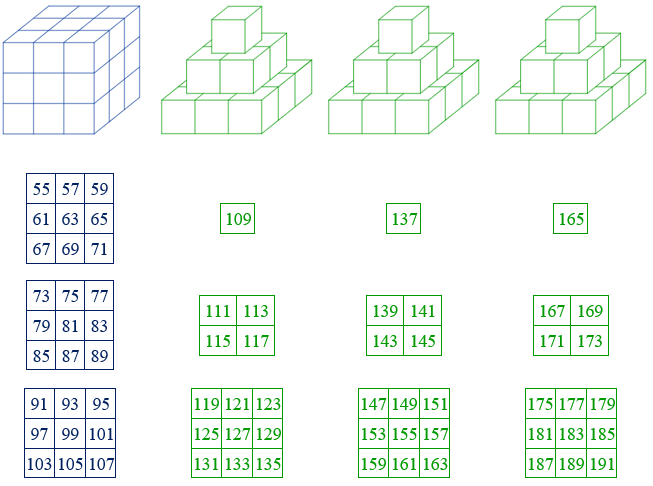
55 + 57 + 59 + . . . + 103 + 105 + 107 = 2187 = 37

 

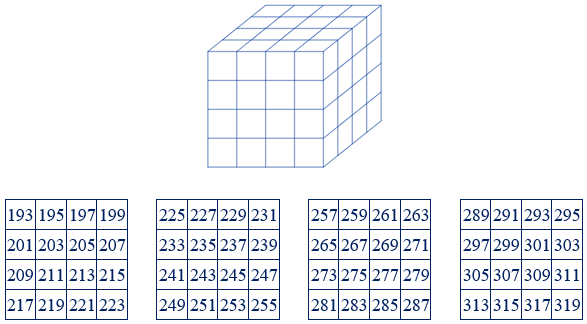
193 + 195 + 197 + . . . + 315 + 317 + 319 = 16384 = 47

 

 

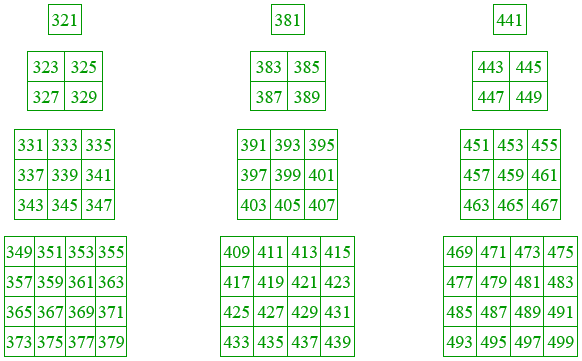
501 + 503 + 505 + . . . + 745 + 747 + 749 = 78125 = 57

 

. . . 

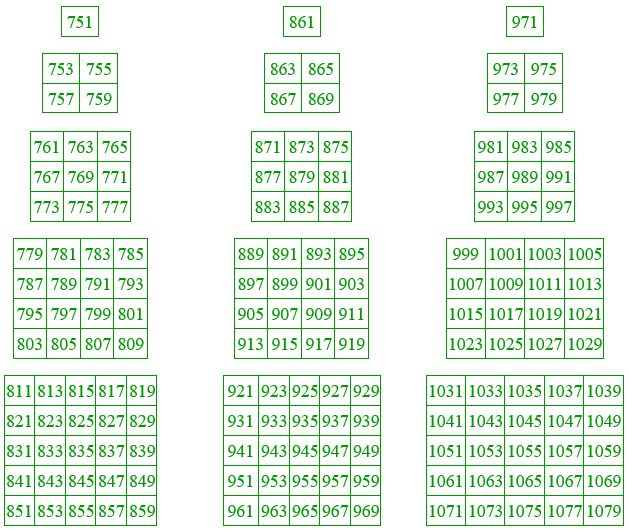
Se puede ampliar la información en el siguiente enlace:

Los números impares y las potencias de los números naturales.

Los números impares y las potencias de los números naturales II.

Número Pi

Aproximaciones de π mediante desarrollo en series de la arcotangente

El profesor de astronomía inglés John Machin, (1680-1751), encuentra un nuevo método para calcular aproximaciones de π, utilizando también el desarrollo en serie de la arcotangente. En 1706, consiguió 100 decimales calculados a mano con la fórmula:

El matemático suizo Leonhard Euler, (1707-1783), en 1764, calculó en una hora veinte cifras decimales del número π con la fórmula:

El matemático alemán Karl Friedrich Gauss, (1777-1855), también descubrió algunas fórmulas del mismo tipo. Una de las más utilizadas ha sido:

El matemático inglés William Shanks, (1812-1882), dedicó veinte años al cálculo de cifras decimales de π y obtuvo en 1853, 707 decimales, con la fórmula de Machin. Sin embargo, cometió un error en el decimal que ocupaba el lugar 528º y a partir de él, todos los demás estaban mal calculados.

Citas

Jean Baptiste Joseph Fourier

«El estudio profundo de la naturaleza es la fuente más fértil de descubrimientos matemáticos».
 
Jean Baptiste Joseph Fourier.
Auxerre, 21 de marzo de 1768 – París, 16 de mayo de 1830.
Matemático y físico francés.
 
Es conocido por sus Series de Fourier, que consisten en la descomposición de funciones periódicas en series trigonométricas convergentes.

Números / Operaciones curiosas

El número 6174. Constante de Kaprekar.

El número 6174 se conoce como constante de Kaprekar debido al matemático indio que lo descubrió, Dattatreya Ramachandra Kaprekar (1905-1986). Se obtiene a partir de la siguiente secuencia de operaciones:

• Escoge un número de cuatro cifras que no tenga tres ni cuatro cifras iguales. Por ejemplo: 4815.

• Coloca las cuatro cifras en orden descendente. En este caso: 8541.

• Coloca las cuatro cifras en orden ascendente. En este caso: 1458.

• Resta los dos números anteriores. En este caso: 8541–1458=7083.

• Si no sale 6174, repite el procedimiento anterior las veces necesarias con los resultados de las diferencias y, como mucho en siete pasos, obtienes la constante de Kaprekar.

8730–0378=8352.

8532–2358=6174.

Problemas geométricos

Triángulos inscritos es un rectángulo

 

En el rectángulo ABCD, de base b cm y altura a cm, se cogen puntos cualesquiera E y F en uno de los lados y un punto G en cualquier posición del lado opuesto. Se construyen los triángulos DEG y GFC. Calcula la suma de las áreas de estos dos triángulos en función de los lados del rectángulo.

Problemas geométricos

Semicircunferencias en un cuadrado

 

En el cuadrado ABCD de a cm de lado, se cogen puntos cualesquiera E y F en dos lados opuestos. Se trazan cuatro semicircunferencias interiores al cuadrado según se observa en la figura. Calcula la suma de las longitudes de las cuatro semicircunferencias en función del lado del cuadrado.

Problemas de ingenio

Moneda falsa

Se tienen ocho monedas iguales de aspecto y tamaño pero una de ellas tiene un peso distinto, aunque no se sabe si pesa más o menos que las demás.

Utilizando una balanza de dos platillos y realizando tres pesadas, intenta descubrir la moneda falsa.

 

Número Pi

Aproximación de π de Euler

El matemático suizo Leonhard Euler (1707-1783), en 1734, consiguió calcular la suma de los inversos de los cuadrados de los números naturales, obteniendo:

Utilizando el emulador de la calculadora Classwiz fx-570SP X Iberia, podemos obtener el valor de la suma para 10, 100, 1000, 10000, 100000 y 1000000 de sumandos y, posteriormente la aproximación de π:

Descripción general de privacidad

Este sitio web utiliza cookies para que podamos brindarle la mejor experiencia de usuario posible. La información de las cookies se almacena en su navegador y realiza funciones como reconocerlo cuando regresa a nuestro sitio web y ayudar a nuestro equipo a comprender qué secciones del sitio web le resultan más interesantes y útiles.