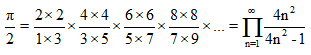Un triángulo escaleno inscrito en un triángulo equilátero

Si ABC es un triángulo equilátero de lado cualquiera, calcula la fracción del área del triángulo equilátero que ocupa el área del triángulo escaleno DEF, sabiendo que AD es la mitad de AB, BE es la cuarta parte de BC, CF es la octava parte de CA.