Un número, su doble y su triple
Calcula los tres primeros números naturales que verifican que su doble es un cuadrado perfecto y su triple es un cubo perfecto.
octubre 2021
Curvas de Plateau
Las curvas de Plateau fueron creadas por el físico belga Joseph Antoine Ferdinand Plateau (1801-1883).
Haz «click» sobre la imagen para abrir la construcción de GeoGebra.
Tangentes a una circunferencia por un punto exterior
Por un punto exterior a una circunferencia se pueden trazar dos rectas tangentes a dicha circunferencia.
Haz «click» sobre la imagen para abrir la construcción con Geogebra y seguirla paso a paso.
¿Posible o imposible?
Repitiendo la modificación del triángulo anterior en los tres lados, se obtiene este nuevo triángulo. ¿Es posible o imposible su construcción en tres dimensiones?
Criterio de divisibilidad del número 7
En los libros de texto se indican los criterios de divisibilidad de los números 2, 3, 4, 5, 6, 9, 10 y 11. No suele aparecer el criterio de divisibilidad del número 7.
Para ver si un número es divisible por 7 se le resta al número, sin la cifra de las unidades, el doble de la cifra de las unidades. Si el resultado de esta diferencia es 0 o múltiplo de 7, entonces el número es divisible por 7. En caso contario, no lo es.
Ejemplos:
• 168. Se hace la diferencia 16 – 2·8 = 16 – 16 = 0. Como se obtiene 0, el número 168 es divisible por 7.
• 329. Se hace la diferencia 32 – 2·9 = 32 – 18 = 14. Como se obtiene un múltiplo de 7, el número 329 es divisible por 7.
• 541. Se hace la diferencia 54 – 2·1 = 54 – 2 = 52. Como no se obtiene un múltiplo de 7, el número 541 no es divisible por 7.
Más por menos. Capítulo 10
Un número llamado e.
Las matemáticas están más cerca de todos nosotros de lo que pensamos. ‘Más por menos’ ofrece explicaciones sencillas y didácticas sobre conceptos matemáticos y su correspondencia con la realidad, sin ser necesaria una formación previa para entender los conceptos explicados. Esta serie consta de trece capítulos y fue emitida por rtve en el programa «La aventura del saber».
Haz click sobre la imagen inferior para verlo.
Trapezoide inscrito en una circunferencia
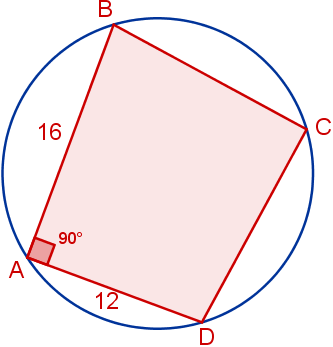
Calcula la superficie del trapezoide de la figura sabiendo que, el ángulo de vértice el punto A es recto, el lado AB mide 16 cm, el lado AD mide 12 cm y los lados CB y CD tienen la misma longitud.
Cuatro números
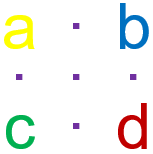
Resuelve el sistema de ecuaciones:
a · b = 180 , a · c = 216 , a · d = 240 , b · c · d = 5400
Remolinos
M.C. Escher. Remolinos. 1957.
Xilografía.
Copo de nieve de Koch
Uno de los fractales más conocidos es el Copo de nieve de Koch. Su descubrimiento se debe al matemático sueco Helge Von Koch (1870-1924) en el año 1904.
Para comprender su formación, a partir de un segmento se realizan de forma indefinida los siguientes pasos, repitiendo en cada uno de los nuevos segmentos que se obtienen el primer paso (n=1).
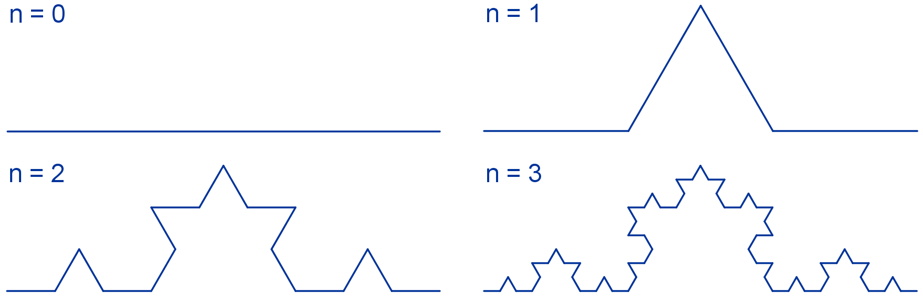
Si esta construcción se realiza en los tres lados de un triángulo equilátero se obtiene el Copo de nieve de Koch.
Haz «click» sobre la imagen para abrir la construcción con Geogebra y seguirla paso a paso.
