Organizando la convención.
La sucesión de Pell es una sucesión recurrente de números naturales dada por:
a1 = 1 , a2 = 2 , an = an–2 + 2·an–1
El primer término es igual a 1, el segundo término es igual a 2 y, a partir del tercero, cada término se obtiene sumando al antepenúltimo el doble del último.
| a3=a1+2a2=1+4=5 | a4=a2+2a3=2+10=12 | a5=a3+2a4=5+24=29 | a6=a4+2a5=12+58=70 |
| a7=a5+2a6=169 | a8=a6+2a7=408 | a9=a7+2a8=985 | a10=a8+2a9=2378 |
Los quince primeros términos de la sucesión son:
1, 2, 5, 12, 29, 70, 169, 408, 985, 2378, 5741, 13860, 33461, 80782, 195025, …
Esta sucesión se debe al matemático británico John Pell (1611-1685).
Se puede obtener la sucesión de Pell de forma gráfica con las longitudes de los lados de la siguiente sucesión de cuadrados.
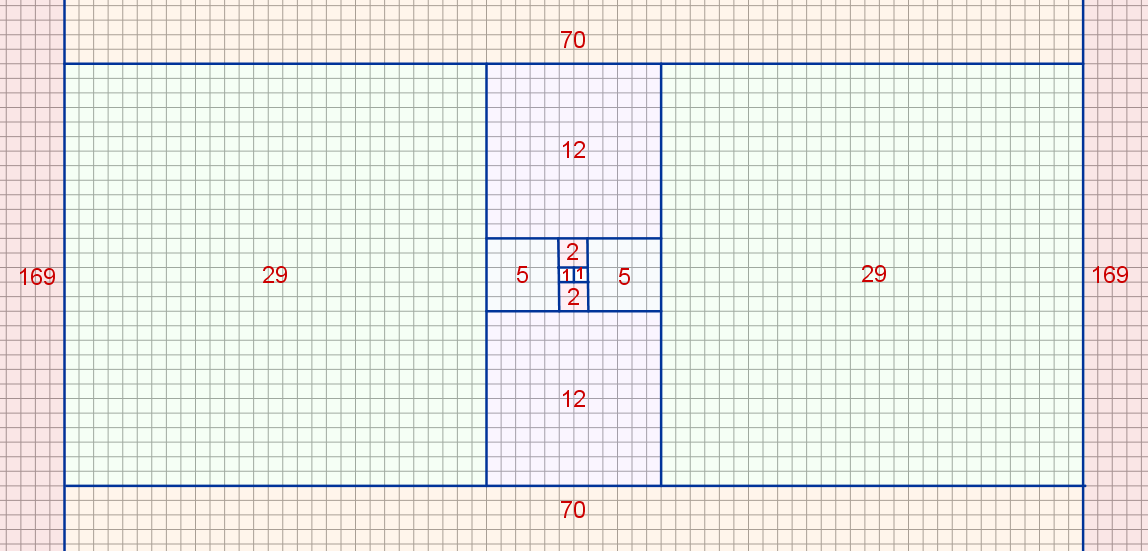
Calcula la longitud de la línea poligonal roja sabiendo que los lados del rectángulo miden 12 cm y 9 cm.
En mi colección de sellos he observado que:
• El 
del total de sellos no son españoles.
• El 
del total de sellos son nuevos.
Averigua cuántos sellos tengo sabiendo que son más de 4000 y menos de 5000.
Coloca los números 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 y 12 en los círculos para que la suma de los cuatro círculos situados en cada uno de los lados de los triángulos equiláteros sea la misma.
(Haciendo «click» sobre la imagen puedes practicar con el juego realizado en GeoGebra).
La recta tangente es la recta perpendicular por el punto P al radio que une P con el centro.
Haz «click» sobre la imagen para abrir la construcción con Geogebra y seguirla paso a paso.
La curva mariposa (butterfly curve) fue descubierta por el matemático estadounidense Temple H. Fay (1940-).
Haz «click» sobre la imagen para abrir la construcción de GeoGebra.
Otro triángulo posible de dibujar en dos dimensiones, pero imposible de construir en tres dimensiones.
