Reptiles
M.C. Escher. Reptiles. 1939.
Tinta india, lápiz y acuarela.
Curso 2017/18. 4º E.S.O. A.
Curso 2021/22. 3º E.S.O. B.
abril 2022
Potencias de exponente negativo del número de oro
Sabiendo que:
se puede obtener la sucesión de potencias de exponente negativo del número de oro:
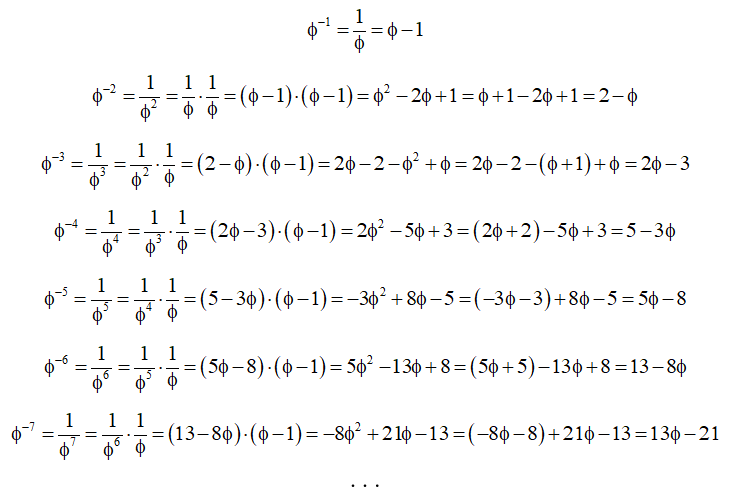
En esta sucesión de potencias se observa que:
• el valor absoluto de los coeficientes de f y los términos independientes son los términos de la sucesión de Fibonacci.
• cualquier potencia de exponente entero, positivo o negativo, se obtiene sumando las dos anteriores, igual que sucede con la construcción de la sucesión de Fibonacci.
René Descartes
«En mi opinión, todas las cosas en la naturaleza ocurren matemáticamente».
René Descartes.
Touraine, 31 de marzo de 1596 – Estocolmo, 11 de febrero de 1650.
Filósofo, Matemático y Físico francés. Como filósofo su obra más conocida el «Discurso del Método» y su frase más célebre «Pienso, luego existo».
Como matemático le debemos la Geometría con coordenadas, los ejes cartesianos se llaman así por él. También la utilización de las letras x, y, z para representar las cantidades desconocidas de una ecuación.
Cuadrado y trapezoide
Calcula la razón entre el área del trapezoide y el área del cuadrado.
0, 1, 2 y 3 cuatros
¿Cuántos números de tres cifras tienen tres cuatros?
¿Cuántos números de tres cifras tienen dos cuatros?
¿Cuántos números de tres cifras tienen un cuatro?
¿Cuántos números de tres cifras no tienen ningún cuatro?
Comiendo pizza moderadamente
Un cliente en un restaurante pide una pizza para cenar.
• Camarero: ¿La quiere cortada en seis o en ocho trozos?
• Cliente: En seis trozos, no tengo mucha hambre y ocho serían muchos.
Reptiles M.C. Escher
Este mosaico fue creado por el artista neerlandés Maurits Cornelis Escher. Se obtiene a partir del recubrimiento del plano con hexágonos.
La siguiente aplicación de GeoGebra es una adaptación de la miscelánea «Mosaicos de Escher«, de la Red Educativa Digital Descartes, realizada por el profesor Enrique Martínez Arcos.
Haz «click» sobre la imagen para abrir la construcción con GeoGebra y seguirla paso a paso.
En la siguiente imagen se puede comprobar el recubrimiento del plano con los reptiles de Escher.
Hueso nazarí
Es otro de los mosaicos más conocidos de la Alhambra. Se obtiene a partir del recubrimiento del plano con cuadrados.
Haz «click» sobre la imagen para abrir la miscelánea del Proyecto Descartes.
Haz «click» sobre la imagen para abrir la construcción con GeoGebra y seguirla paso a paso.
Pajarita nazarí
Es uno de los mosaicos más conocidos y más utilizados en la Alhambra. Se obtiene a partir del recubrimiento del plano con triángulos equiláteros.
Haz «click» sobre la imagen para abrir la miscelánea del Proyecto Descartes.
Haz «click» sobre la imagen para abrir la construcción con GeoGebra y seguirla paso a paso.
Mosaicos
Si se quiere recubrir el plano con polígonos regulares iguales, solo se puede hacer utilizando triángulos equiláteros, cuadrados y hexágonos, según se puede comprobar en la imagen siguiente.
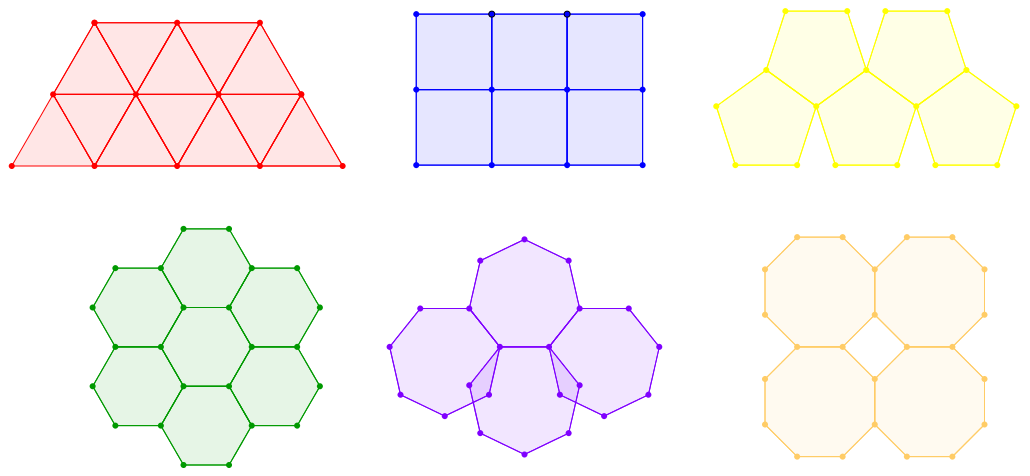
Para que se pueda recubrir con polígonos regulares iguales, en cada vértice tienen que concurrir el mismo número de polígonos, sin dejar huecos (como sucede con los pentágonos) y sin que haya solapamiento (como sucede con los heptágonos). Por tanto, la medida del ángulo interior de cada polígono regular tiene que ser divisor de 360º. Los polígonos que verifican esta propiedad son el triángulo equilátero (60º), el cuadrado (90º) y el hexágono (120º).
