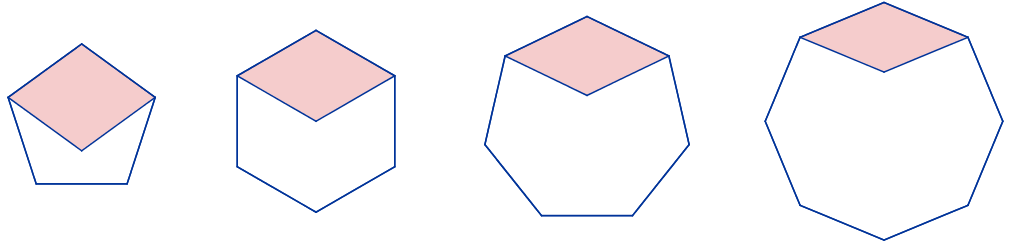
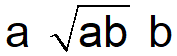Trapecios poligonales
Se construyen trapecios utilizando cuatro vértices consecutivos de polígonos regulares de 1 cm de lado, según se observa en las figuras siguientes.

• Calcula la superficie de los trapecios anteriores.
• Deduce una expresión para la superficie del trapecio de cualquier polígono regular en función del número de lados.