Cuadrado y circunferencias
 |
Calcula la longitud del radio de las circunferencias inscritas al cuadrado y de la circunferencia central, sabiendo que el lado del cuadrado mide 1 cm. |  |
febrero 2023
Número polidivisible y poliprimo
Calcula un número de seis cifras distintas:
que verifica:
| • El número A es divisible por 1. | • El número ABCDEF es primo. |
| • El número AB es divisible por 2. | • El número BCDEF es primo. |
| • El número ABC es divisible por 3. | • El número CDEF es primo. |
| • El número ABCD es divisible por 4. | • El número DEF es primo. |
| • El número ABCDE es divisible por 5. | • El número EF es primo. |
| • El número F es primo. |
Deltoides con proporciones áureas
En la sección sobre el número de oro se han construido dos triángulos isósceles con proporciones áureas. Son triángulos semejantes a los dos siguientes. Se escogen como longitudes de los lados 1, Φ y Φ2, para comprender mejor la construcción y las proporciones que existen.
Con estos dos triángulos se pueden construir los siguientes deltoides:
• El primero se obtiene uniendo los dos triángulos isósceles. Es un deltoide convexo. El cociente entre el lado mayor y la diagonal menor y el cociente entre la diagonal menor y el lado menor es el número de oro.
• El segundo se obtiene quitando del primero, un triángulo igual al segundo. Es un deltoide cóncavo. El cociente entre el lado mayor y la diagonal menor y el cociente entre la diagonal menor y el lado menor es el número de oro.
• El tercero se obtiene uniendo dos triángulos como el primero por su lado mayor. Es un deltoide convexo. El cociente entre el lado mayor y el lado menor es el número de oro.
• El cuarto se obtiene uniendo dos triángulos como el segundo por su lado menor. Es un deltoide cóncavo. El cociente entre el lado mayor y el lado menor es el número de oro.
Deltoides semejantes a estos los podemos encontrar en el pentágono regular y en el decágono regular, utilizando las diagonales y sus puntos de intersección. A continuación se representan los de mayor tamaño, pero es posible encontrar otros de menor tamaño en el decágono.
Grafo hamiltoniano
Un camino es simple si no repite vértices. Un camino simple que contiene todos los vértices del grafo es un camino hamiltoniano.
Un ciclo es un camino cerrado en el que los únicos vértices repetidos son el primero y el último.
Un grafo hamiltoniano es un grafo que contiene un ciclo hamiltoniano.
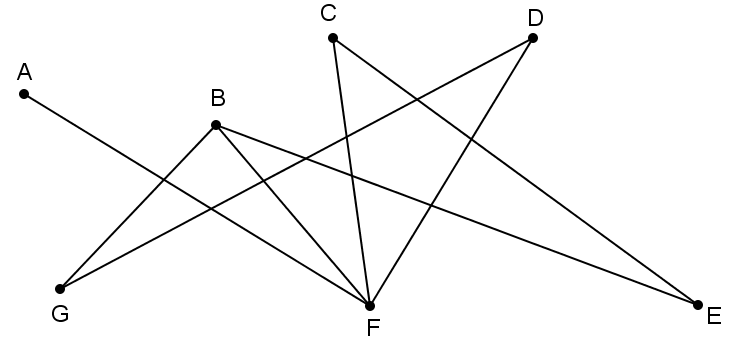
En el grafo siguiente, un camino hamiltoniano es el formado por las aristas AF, FC, CE, EB, BG, GD. Sin embargo, no existe un ciclo hamiltoniano. Por tanto, no es un grafo hamiltoniano.
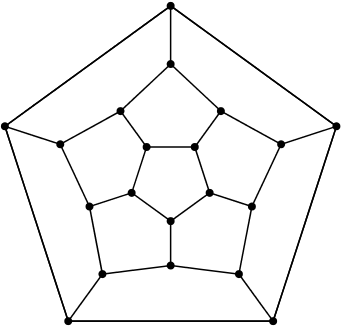
El grafo siguiente, que se obtiene a partir del dodecaedro del viajero, si contiene un ciclo hamiltoniano, que tienes que encontrar como solución al problema. Por tanto, este grafo sí es un grafo hamiltoniano.
Hexágono y circunferencias II
 |
Calcula la longitud del radio de las circunferencias inscritas al hexágono, sabiendo que el lado del hexágono mide 1 cm. |  |
Número poliprimo
Calcula un número de ocho cifras distintas y no nulas:
que verifica:
| • El número ABCDEFGH es primo. | • El número EFGH es primo. |
| • El número BCDEFGH es primo. | • El número FGH es primo. |
| • El número CDEFGH es primo. | • El número GH es primo. |
| • El número DEFGH es primo. | • El número H es primo. |
¿Puede existir un número poliprimo con nueve cifras distintas y no nulas?
Lucio Anneo Séneca
«Jamás se descubriría nada si nos considerásemos satisfechos con las cosas descubiertas».
Lucio Anneo Séneca.
Córdoba, 4 a.C. – Roma, 65 d. C.
Filósofo, político, orador y escritor romano.
¿Cuántas personas se llaman como tú?
Haciendo «click» sobre el enlace o sobre la imagen, puedes comprobar cuántas personas hay en España con tu mismo nombre o con tus mismos apellidos, así como la distribución, en tanto por mil, por provincias.
La página corresponde el Instituto Nacional de Estadística (
).
https://www.ine.es/widgets/nombApell/index.shtml
Octógono y circunferencias
Las cuatro circunferencias tienen el mismo radio, son tangentes a las circunferencias contiguas y son tangentes a los lados del octógono. Si el lado del octógono mide 1 centímetro, calcula el radio de las circunferencias.
Número polidivisible
Calcula un número de nueve cifras distintas:
que verifica:
| • El número A es divisible por 1. | • El número ABCDEF es divisible por 6. |
| • El número AB es divisible por 2. | • El número ABCDEFG es divisible por 7. |
| • El número ABC es divisible por 3. | • El número ABCDEFGH es divisible por 8. |
| • El número ABCD es divisible por 4. | • El número ABCDEFGHI es divisible por 9. |
| • El número ABCDE es divisible por 5. |
