Resolviendo problemas matemáticos – laborales
Una solución meditada.
febrero 2023
Cuadrado de la suma y suma de los cubos
Una curiosa e interesante propiedad de los números naturales. El cuadrado de la suma de los n primeros números naturales es igual a la suma de los cubos de dichos números.
( 1 + 2 + 3 + … + n )2 = 13 + 23 + 33 + … + n3
Comprobación para n=1, 2, 3, 4 y 5:
| 12=1 | 13=1 |
| (1+2)2=32=9 | 13+23=1+8=9 |
| (1+2+3)2=62=36 | 13+23+33=1+8+27=36 |
| (1+2+3+4)2=102=100 | 13+23+33+43=1+8+27+64=100 |
| (1+2+3+4+5)2=152=225 | 13+23+33+43+53=1+8+27+64+125=225 |
| . . . | . . . |
Demostración gráfica para n=4.
 |
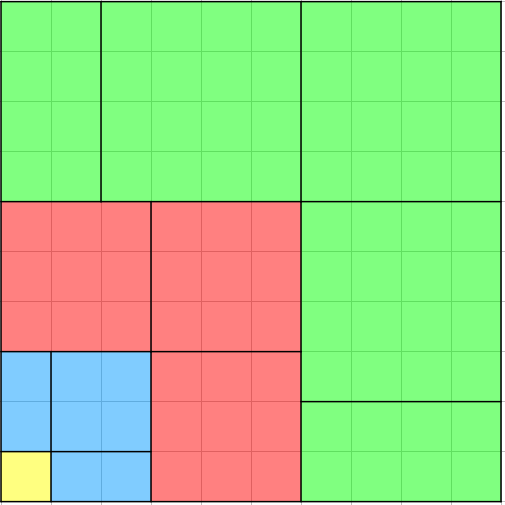La longitud del lado del cuadrado completo es: 1+2+3+4=10. El área del cuadrado completo es: (1+2+3+4)2=102=100. |
| Hay un cuadrado de lado 1. Su área es 1. | |
| Juntando las dos mitades, hay dos cuadrados de lado 2. El área de los dos es 2·22=23. | |
| Hay tres cuadrados de lado 3. El área de los tres es 3·32=33. | |
| Juntando las dos mitades, hay cuatro cuadrados de lado 4. El área de los cuatro es 4·42=43. | |
| El área del cuadrado completo, sumando las área de todos los cuadrados es: 1·12+2·22+3·32+4·42=13+23+33+43=1+8+27+64=100. |
Hexágono y circunferencias
Las tres circunferencias tienen el mismo radio, son tangentes dos a dos y son tangentes a los lados del hexágono. Si el lado del hexágono mide 1 centímetro, calcula el radio de las circunferencias.
Congreso internacional
• A un congreso internacional asisten científicos de España, Italia y Alemania. Se elige un grupo de científicos para realizar un determinado estudio y se observa que, en dicha comisión, todos son españoles menos dos, todos son italianos menos dos y todos son alemanes menos dos. ¿Cuántas personas de cada país forman la comisión?
• A un congreso internacional asisten científicos de España, Italia, Alemania y Portugal. Se elige un grupo de científicos para realizar un determinado estudio y se observa que, en dicha comisión, todos son italianos menos seis, todos son alemanes menos seis y todos son portugueses menos seis. Los demás son españoles. Indica la composición de todas las posibles comisiones.
• A un congreso internacional asisten científicos de España, Italia, Alemania, Portugal y Francia. Se elige un grupo de científicos para realizar un determinado estudio y se observa que, en dicha comisión, todos son italianos menos diez, todos son alemanes menos diez, todos son portugueses menos diez y todos son franceses menos diez. Los demás son españoles. Indica la composición de todas las posibles comisiones.
