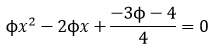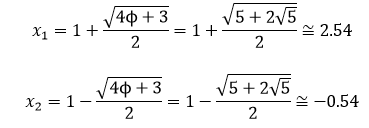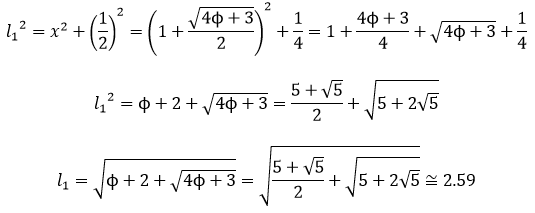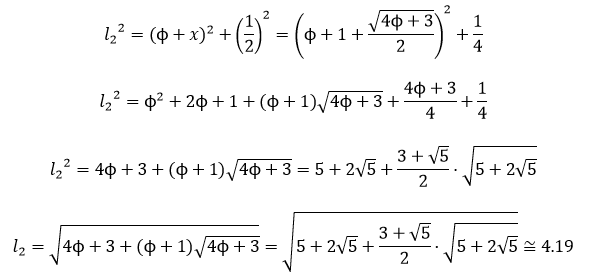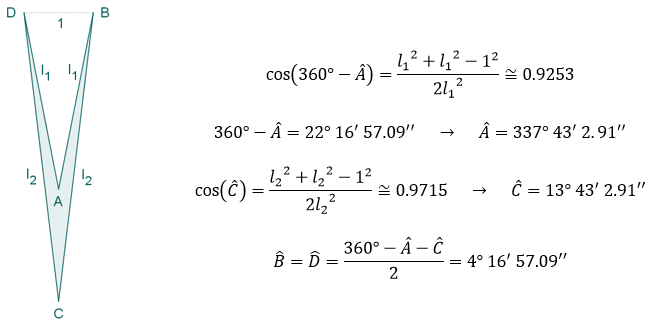Se construye un hexágono regular prolongando lados alternos de un dodecágono regular.
• Calcula la razón entre el área del hexágono y el área del dodecágono.
• Calcula la razón entre el perímetro del hexágono y el perímetro del dodecágono.
Se construye un pentágono regular prolongando lados alternos de un decágono regular.
• Calcula la razón entre el área del pentágono y el área del decágono.
• Calcula la razón entre el perímetro del pentágono y el perímetro del decágono.
Calcula un número de seis cifras:
que verifica:
• Contiene todas las cifras impares al menos una vez.
• Es múltiplo de 3.
• Las dos cifras iguales son la media aritmética de las cifras que tienen a su izquierda y a su derecha.
• Las dos cifras centrales forman un número que no es primo, siendo la tercera mayor que la cuarta.
Una vez que se ha demostrado la existencia del deltoide áureo cóncavo en el que su eje de simetría coincide con su diagonal mayor, veamos la forma de construirlo gráficamente.
Haz «click» sobre la imagen para abrir la construcción de GeoGebra.
Cálculo de las longitudes de los lados y medida de los ángulos del deltoide en el que su eje de simetría coincide con su diagonal mayor
Para calcular los lados del deltoide áureo empezamos calculando la distancia x de la figura. Para ello se necesita calcular los lados l1 y l2 en función de x y después imponer la condición de que el cociente entre el lado mayor y el lado menor es el número de oro.
Se debe verificar que:
Se sustituye Φ2 por Φ+1 :
Se obtiene una ecuación parecida a la obtenida para calcular la longitud de los lados del deltoide áureo convexo. La única diferencia es el cambio del signo del coeficiente de x, por tanto, las soluciones de esta ecuación serán las opuestas de la ecuación resuelta en dicho apartado:
En este caso consideramos también la solución positiva. Pero se observa que en la búsqueda del deltoide áureo convexo se obtiene también el deltoide áureo cóncavo y recíprocamente.
La longitud del lado l1 será:
La longitud del lado l2 será:
Cálculo de los ángulos:
El perímetro y el área de este deltoide son, respectivamente:
Si intentamos construir un deltoide cóncavo cuyos lados estén en proporción áurea, por ejemplo, cuyos lados midan 1 y Φ, nos encontramos que existen infinitas posibilidades. He aquí algunos ejemplos.
Todos tienen el mismo perímetro, P=2+2Φ u, pero distinta superficie.
Si intentamos construir un deltoide cuyas diagonales estén en proporción áurea, tenemos también infinitas posibilidades. A continuación, se muestran algunos. Los deltoides están construidos utilizando un rectángulo áureo de referencia.
Si el eje de simetría del deltoide es su diagonal mayor.
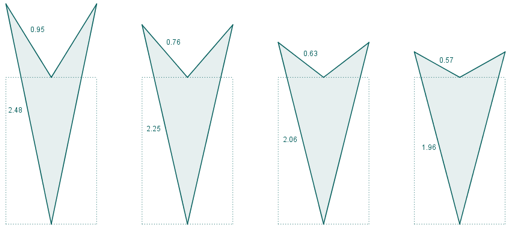
Si el eje de simetría del deltoide es su diagonal menor.
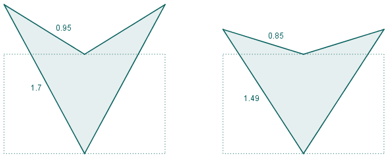
Todos tienen en común que el cociente entre sus diagonales es el número de oro. También todos tienen igual área, pero distinto perímetro.
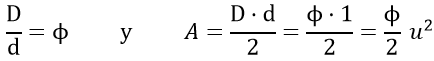
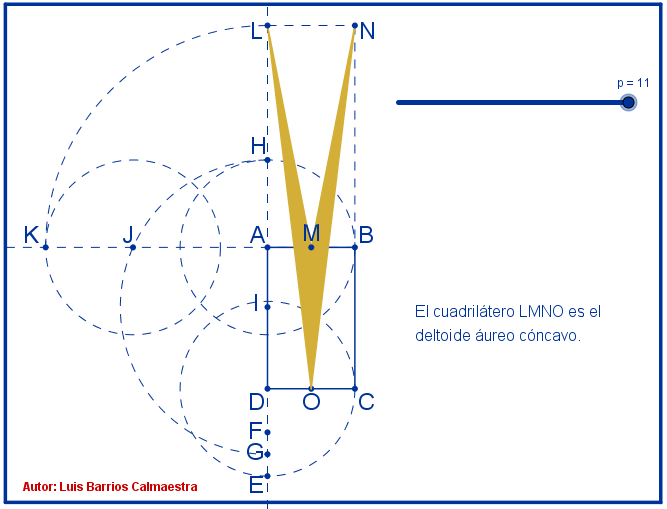
Existen tres deltoides cóncavos cuyos lados y cuyas diagonales están en proporción áurea, uno en el que su eje de simetría es su diagonal mayor y dos en los que el eje de simetría es su diagonal menor.
Se construye un cuadrado prolongando lados alternos de un octógono regular.
• Calcula la razón entre el área del cuadrado y el área del octógono.
• Calcula la razón entre el perímetro del cuadrado y el perímetro del octógono.
Calcula un número de seis cifras:
que verifica:
• Ninguna cifra es impar.
• La primera es un tercio de la quinta más la mitad de la tercera.
• La segunda es la menor de todas.
• La última es la diferencia entre la cuarta y la quinta.
La siguiente aplicación permite resolver un problema de combinatoria respondiendo a las preguntas que se plantean y deslizando el punto por el deslizados inferior para realizar los cálculos.
Haz «click» sobre la imagen para acceder.
