Jean Philippe Rameau


La Sociedad de Educación Matemática de la Comunidad Valenciana «Al Khwarizmi» publica la quinta página de su Calendario Matemático anual, correspondiente al mes de enero el curso 2023-24. Los problemas de los días 17-18 y 19-20 corresponden a actividades de este blog.
Se puede acceder a la publicación haciendo «click» sobre la imagen siguiente.
En cada instante del día se representa por «hh» la hora, por «mm» los minutos y por «ss» los segundos. ¿En cuántos instantes de cada día se verifica la siguiente relación?

Si unimos dos las actividades de la entrada «Feliz 2024«.
Suma de sus cifras: 2 + 0 + 2 + 4 = 8
Suma de los cuadrados de sus cifras: 22 + 02 + 22 + 42 = 24
• ¿Cuál fue el año anterior a 2024 en el que la suma de sus cifras es 8 y la suma de los cuadrados de sus cifras coincide con las dos últimas cifras del número?
• ¿Cuál será el año siguiente a 2024 en el que la suma de sus cifras es 8 y la suma de los cuadrados de sus cifras coincide con las dos últimas cifras del número?
• Cuadrado mágico aditivo de orden 4 con constante mágica 2024.
Los números utilizados:
326 – 350 – 374 – 398 – 422 – 446 – 470 – 494 – 518 – 542 – 566 – 590 – 614 – 638 – 662 – 686
forman una progresión aritmética con diferencia d=24.
La suma de los números de cada fila, de cada columna y de las dos diagonales es igual a 2024. Además, tiene las propiedades del cuadrado mágico conocido como Chautisa Yantra.

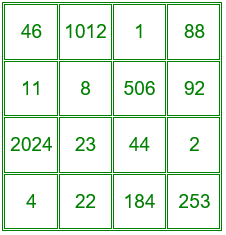
• Cuadrado mágico multiplicativo de orden 4 con constante mágica 20242.
Con los 16 divisores de 2024 se puede construir un cuadrado mágico multiplicativo de orden 4 con constante mágica 20242.
El producto de los números de cada fila, de cada columna y de las dos diagonales es igual a 20242. Además, tiene las propiedades del cuadrado mágico conocido como Chautisa Yantra, multiplicando en lugar de sumando.
¡ FELIZ 2024 !
2024 = ( 21 + 23 ) · ( 22 + 24 )
• Descomposición factorial: 2024 = 23 × 11 × 23
• El número 2024 se puede expresar como diferencia de cuadrados y, por tanto, como producto de una suma por una diferencia:
2024 = 2025 – 1 = 452 – 12 = (45-1)·(45+1) = 44·46
• Número de divisores: (3+1)·(1+1)·(1+1) = 4·2·2 = 16.
• Suma de sus cifras: 2 + 0 + 2 + 4 = 8
• Suma de los cuadrados de sus cifras: 22 + 02 + 22 + 42 = 24
• Operaciones curiosas con resultado 2024:
22 + 42 + 62 + 82 + 102 + 122 + 142 + 162 + 182 + 202 + 222 = 2024
23 + 33 + 43 + 53 + 63 + 73 + 83 + 93 = 2024
• El año 2024 es un año bisiesto. Son años bisiestos los múltiplos de 4, pero hay algunas excepciones. ¿Qué años son múltiplos de 4 y no son bisiestos?
• El número 2024 se escribe uniendo dos múltiplos de 4 consecutivos, 20 y 24. ¿Cuáles fueron los tres años anteriores a 2024 con esta propiedad? ¿Cuáles serán los tres años siguientes con esta propiedad? ¿Cada cuántos años sucede esto? ¿Por qué?
• La suma de las cifras del número 2024 es 8. ¿Cuáles fueron los cinco años anteriores a 2024 con esta propiedad? ¿Cuáles serán los cinco años siguientes con esta propiedad?
• La suma de los cuadrados de las cifras del número 2024 es 24. ¿Cuáles fueron los tres años anteriores a 2024 con esta propiedad? ¿Cuáles serán los tres años siguientes con esta propiedad?
• La suma de los cuadrados de las cifras del número 2024 coincide con las dos últimas cifras del número, 24. ¿Cuál fue el año anterior a 2024 con esta propiedad? ¿Cuál será el año siguiente con esta propiedad?
• El número 2024 se obtiene restando uno a un cuadrado perfecto 2024=2025–1=452–1. ¿Cuáles fueron los tres años anteriores a 2024 con esta propiedad? ¿Cuáles serán los tres años siguientes con esta propiedad? ¿Cada cuántos años sucede esto?
• El número 2024 se puede expresar como el producto de dos números pares consecutivos, 2024=44·46. ¿Cuáles fueron los tres años anteriores a 2024 con esta propiedad? ¿Cuáles serán los tres años siguientes con esta propiedad? ¿Cada cuántos años sucede esto?
• Escribimos la fecha de un día cualquiera del año con el formato “dd/mm/aa”, es decir, dos cifras para el día del mes, dos cifras para el mes y dos cifras para el año. ¿Qué días del año verifican “dd+mm=aa”? ¿Qué días del año verifican “dd·mm=aa”?
• El año 2024 comienza en lunes y termina en martes. ¿Cuál será el próximo año que empiece en lunes y termine en martes?
Tiene 16 divisores: 1, 2, 4, 8, 11, 22, 23, 44, 46, 88, 92, 184, 253, 506, 1012 y 2024. Es un número abundante, la suma de sus divisores, excepto el mismo número, es mayor que el número:
1+2+4+8+11+22+23+44+46+88+92+184+253+506+1012 = 2296 > 2024
• Es un número infeliz, no se obtiene 1 al final de la secuencia de operaciones:

• Pero sin embargo es un número que transmite alegría o número de Harshad, porque es divisible por la suma de sus cifras:
![]()
Pero, independientemente de lo que digan las Matemáticas de este número,
¡ Feliz 2024 !