Números curiosos de cuatro cifras VI
Calcula, sin ayuda de tecnología, todos los números naturales de cuatro cifras, iguales o distintas, pero no nulas, abcd, que verifican:
a × b × c = d
noviembre 2024
Mosaico con octógonos y cuadrados
Si en un mosaico de baldosas cuadradas cortamos un cuadrado en cada vértice, de forma que sus vértices estén sobre las aristas de los cuadrados iniciales, se obtiene un nuevo mosaico con octógonos y cuadrados.
En la primera imagen se puede observar un mosaico en la entrada de un edificio en Berlín. En este mosaico los octógonos que se forman no tienen los lados iguales, son octógonos irregulares.
En la segunda imagen se puede observar un mosaico situado en una plaza de Otívar, en la provincia de Granada. En este mosaico los octógonos que se forman tienen los lados iguales, son octógonos regulares.
Haz «click» sobre la imagen para comprobar, con una escena del Proyecto Descartes, como cambia el mosaico al modificar la medida de la mitad de la diagonal del cuadrado menor. Lee el apartado indicaciones ¿Qué sucede para los valores 0 y 1? ¿Para qué valores se obtendrán octógonos regulares?
Área de un deltoide
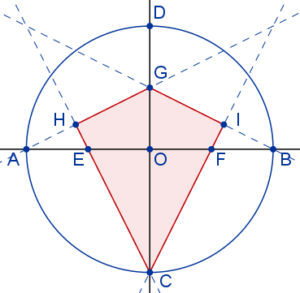
1. Se representa una circunferencia con centro el punto O y una unidad de radio.
2. Se trazan dos diámetros perpendiculares. Sean A y B los puntos de corte de la circunferencia con uno de los diámetros. Sean C y D los puntos de corte de la circunferencia con el otro diámetro.
3. Se representan los puntos medios E, F y G de los radios OA, OB y OD respectivamente.
4. Se traza la recta que pasa por los puntos G y A. Se traza también la recta que pasa por los puntos G y B.
5. Por el punto C se trazan perpendiculares a ambas rectas que las cortan en los puntos H e I respectivamente.
6. Calcula el perímetro y la superficie del deltoide CHGI, expresando los resultados con fracciones y raíces si fuese necesario.
Números curiosos de cuatro cifras V
Calcula, sin ayuda de tecnología, todos los números naturales de cuatro cifras distintas, abcd, que verifican:
a × b = c × d
¡ Gracias Rafa !
El 19 de noviembre de 2024 finalizó su carrera deportiva el tenista Rafa Nadal. Sin duda, el mejor deportista español de todos los tiempos y uno de los mejores tenistas del mundo, siendo el mejor en tierra batida.
Un deportista con unos valores extraordinarios dentro y fuera de la pista, admirado y respetado por todos los aficionados al deporte. Ha sido y será modelo de inspiración para jóvenes y mayores.
¡ GRACIAS RAFA !
Estos son sus logros deportivos:
¡ 0 raquetas destrozadas !
1080 victorias (82.63%) y 227 derrotas (17.37%)
208 semanas como número 1 de la ATP
Medalla de oro individual en los Juegos Olímpicos de Pekín de 2008.
Imagen de RTVE
Medalla de oro en dobles en los Juegos Olímpicos de Río de Janeiro de 2016. Jugando con Marc López.
22 GRAND SLAM
2 ABIERTOS DE AUSTRALIA. Años: 2009 y 2022.
14 ROLAND GARROS. Años: 2005, 2006, 2007, 2008, 2010, 2011, 2012, 2013, 2014, 2017, 2018, 2019, 2020 y 2022.
2 WIMBLEDON. Años: 2008 y 2010.
4 ABIERTOS DE EEUU. Años: 2010, 2013, 2017 y 2019.
36 MASTER 1000.
3 Indian Wells. Años: 2007, 2009 y 2013.
11 Montecarlo. Años: 2005, 2006, 2007, 2008, 2009, 2010, 2011, 2012, 2016, 2017 y 2018.
5 Madrid. Años: 2005, 2010, 2013, 2014 y 2017.
1 Hamburgo. Años: 2008.
10 Roma. Años: 2005, 2006, 2007, 2009, 2010, 2012, 2013, 2018, 2019 y 2021.
5 Canadá (Toronto o Montreal). Años: 2005, 2008, 2013, 2018 y 2019.
1 Cincinnati. Año 2013.
23 ATP 500
1 Rio de Janeiro. Año: 2014.
4 Acapulco. Años: 2005, 2013, 2020 y 2022.
1 Dubái. Año: 2006.
12 Barcelona. Años: 2005, 2006, 2007, 2008, 2009, 2011, 2012, 2013, 2016, 2017, 2018 y 2021.
2 Stuttgart. Años: 2005 y 2007.
1 Hamburgo. Año: 2015.
1 Pekín. Año: 2017.
1 Tokio. Año: 2010.
10 ATP 250
1 Doha. Año: 2014.
1 Melbourne. Año: 2022.
1 Buenos Aires. Año: 2015.
2 Brasil. Años: 2005 y 2013.
1 Halle. Año: 2015.
1 Queen’s Club. Año: 2008.
1 Bástad. Año: 2005.
1 Sopot. Año: 2004.
1 Pekín. Año: 2005.
5 COPA DAVIS
Años: 2004, 2008, 2009, 2011 y 2019.
2 COPA LAVER
Años: 2017 y 2019.
Premio Príncipe de Asturias de los Deportes. Año: 2008
Premio Laureus al Deportista Revelación. Año: 2006
Premio Laureus al mejor deportista. Años: 2011 y 2021
Premio Laureus a la mejor reaparición. Año: 2014
David Hilbert
«Un problema matemático ha de ser difícil para que nos atraiga, pero no completamente inaccesible, para evitar que nuestros esfuerzos sean inútiles».
David Hilbert.
Königsberg, 23 de enero de 1862 – Gotinga, 14 de febrero de 1943.
Matemático alemán.
Se considera el matemático más importante del siglo XX.
Área de un triángulo
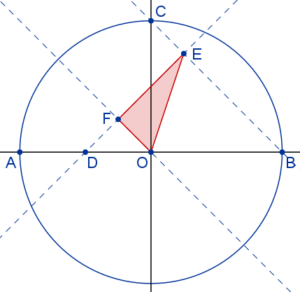
1. Se representa una circunferencia con centro el punto O y una unidad de radio.
2. Se trazan dos diámetros perpendiculares. Sean A y B los puntos de corte de la circunferencia con uno de los diámetros. Sea C uno de los puntos de corte de la circunferencia con el otro diámetro.
3. Se traza la recta que pasa por los puntos B y C. Se traza una una paralela a esta recta por el punto O.
4. Sea D el punto medio de A y O. Se traza la perpendicular por el punto D a las rectas anteriores cortándolas en los puntos E y F.
5. Calcula el perímetro y la superficie del triángulo OEF, expresando los resultados con fracciones y raíces si es necesario.
Números curiosos de cuatro cifras IV
Calcula, sin ayuda de tecnología, todos los números naturales de cuatro cifras distintas, abcd, que verifican:
ac × bd = db × ca
Ternas pitagóricas
Una terna pitagórica es un grupo de tres números naturales a, b y c que verifican: a2=b2+c2. Es decir, tres números naturales que pueden ser las medidas de los lados de un triángulo rectángulo y que, por tanto, verifican el Teorema de Pitágoras.
Es muy conocida la terna pitagórica formada por los números 5, 4 y 3, e incluso la formada por 13, 12 y 5. También que los múltiplos de una terna pitagórica también forman una terna pitagórica. Pero, ¿cuántas ternas pitagóricas existen?
Ya se ha incluido anteriormente otra entrada sobre este tema en este blog realizada con GeoGebra. Ahora se presenta más completa con una miscelánea del Proyecto Descartes.
Haz «click» sobre la imagen para abrir la miscelánea.
Ecuación de segundo grado
La siguiente aplicación de GeoGebra permite resolver paso a paso una ecuación de segundo grado aplicando la fórmula general. Mueve los puntos por los deslizadores de la parte superior para introducir los coeficientes y el de la parte inferior para seguir los pasos de la solución.
Haz «click» sobre la imagen para acceder.
