30 de mayo

Hoy es viernes 30 de mayo (30/05) de 2025. Hoy es el día 150º (centésimo quincuagésimo) de un año no bisiesto. Un día interesante matemáticamente porque:
30 × 5 = 150
Hay treinta y tres días de cada año no bisiesto con esta propiedad.

Hoy es viernes 30 de mayo (30/05) de 2025. Hoy es el día 150º (centésimo quincuagésimo) de un año no bisiesto. Un día interesante matemáticamente porque:
30 × 5 = 150
Hay treinta y tres días de cada año no bisiesto con esta propiedad.

Se divide una circunferencia de radio 1 cm en tres arcos de longitudes directamente proporcionales a 3, 4 y 5 respectivamente. Sean A, B y C los puntos que separan dichos arcos.
Calcula la medida de los ángulos, la longitud de los lados y la superficie del triángulo ABC, expresando las medidas con fracciones y raíces, sin utilizar números decimales.
Calcula todos los números naturales de cuatro cifras, abcd, que verifican que la suma del primero y el segundo es igual al cociente entre el tercero y el cuarto:
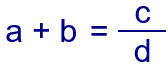
Esta miscelánea del Proyecto Descartes consiste en adivinar un número entre 1 y 1000 en un máximo de diez intentos. Después de cada intento, la escena indicará entre qué números está comprendido el número buscado utilizando los intentos más próximos del participante. Además dispone de un contador de segundos para intentar conseguirlo en el menor tiempo posible.
Haz «click» sobre la imagen y sigue las instrucciones del juego.
Se tiene el eje de abscisas, y=0. Se representa una recta paralela al eje de abscisas, y=k. Sobre el eje de abscisas se representa el origen de coordenadas O:(0,0) y otro punto cualquiera A:(a,0). Sobre la recta paralela se representa el punto de corte con el eje de ordenadas, B:(0,k) y otro punto cualquiera C:(c,k). Los segmentos OC y BA se cortan en el punto E, cuyas coordenadas se desconocen.

Sea T1 el triángulo determinado por los puntos O, A y E. Sea T2 el triángulo determinado por los puntos B, C y E. Calcula el cociente entre las superficies de los triángulos T1 y T2 con el menor número de parámetros posible.
Calcula todos los números naturales de cuatro cifras, abcd, que verifican que la suma del primero y el segundo es igual al producto del tercero y el cuarto:
a + b = c × d

Sea t el triángulo ABC cuyos lados AB, AC y BC son proporcionales a 2, 3 y 4 respectivamente. Se divide el lado AB en dos partes iguales, el lado AC en tres partes iguales y el lado BC en cuatro partes iguales. Se construyen los triángulos t1, t2 y t3 según se observa en la figura.
Calcula el cociente entre la superficie del triángulo t y la suma de las áreas de los triángulos t1, t2 y t3.
Calcula todos los números naturales de tres cifras, abc, que verifican que el producto de las dos primeras cifras es igual al cociente entre la tercera y la primera:

La Sociedad de Educación Matemática de la Comunidad Valenciana «Al Khwarizmi» publica la novena página de su Calendario Matemático anual, correspondiente al mes de mayo del curso 2024-25. Los problemas de los días 12-13 y 23-24 corresponden a actividades de este blog.
Se puede acceder a la publicación haciendo «click» sobre la imagen siguiente.
Según el mensaje recibido del Servicio de Innovación Educativa de la Junta de Andalucía, debido a la falta de mantenimiento y posibles fallos de seguridad de algunos modelos, los temas (formatos) de BlogsAverroes con este problema se eliminarán de la plataforma.
Esto sucede con el Tema (Apariencia) de este blog, por lo que hay que proceder a cambiar su aspecto. Se harán algunas pruebas hasta encontrar una apariencia adecuada entre las posibilidades existentes.
Los contenidos del blog no se verán afectados, pero sí la presentación de los mismos.