Claudi Alsina
«La matemática rigurosa se hace con la mente. La matemática hermosa se enseña con el corazón».
Claudi Alsina Catalá.
Barcelona, 30 de enero de 1952 – Barcelona, 16 de noviembre de 2025.
Profesor de Matemáticas.
noviembre 2025
25 de noviembre
Hoy es martes 25 de noviembre (25/11) de 2025. Hoy es el día 329º (tricentésimo vigesimonoveno) de un año no bisiesto. Faltan 36 días para que acabe el año. Un día interesante matemáticamente porque:
25 + 11 = 36
¿Cuántos días del año tienen esta propiedad?
Hexágono y cuadrado
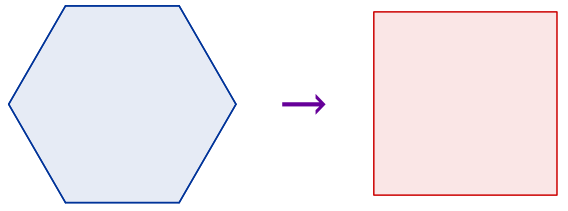
A partir de un hexágono regular cualquiera, construir con regla y compás un cuadrado de igual área que el hexágono.
Operador matemático
El símbolo ∗ representa un operador matemático que realiza diversas operaciones matemáticas con los números que intervienen devolviendo el resultado que se muestra en cada ejemplo.
| 2 ∗ 2 = 3 | 3 ∗ 3 = 8 | 4 ∗ 4 = 15 |
| 3 ∗ 2 = 4 | 3 ∗ 4 = 12 | 4 ∗ 3 = 10 |
Averigua como actúa y calcula:
| 5 ∗ 7 | 7 ∗ 5 | a ∗ b |
¿Para qué parejas de números se verifica la propiedad conmutativa con este operador?
Cuadrado y triángulo
A partir de un cuadrado cualquiera, construir con regla y compás un triángulo equilátero de igual área que el cuadrado. Puedes utilizar las construcciones geométricas de «Operaciones con segmentos«.
Números primos gemelos, trillizos y otros
a) ¿Pueden existir dos números consecutivos que sean primos? ¿Pueden existir tres números consecutivos que sean primos? En caso afirmativo a algunas de las preguntas anteriores, encuentra todos los casos en los que los números primos son menores que 100.
b) Dos números primos son primos gemelos si se diferencian en dos unidades, es decir si son dos números impares consecutivos. Encuentra todas las parejas de primos gemelos menores que 100.
c) Un número primo es un primo aislado si no pertenece a ninguna pareja de primos gemelos. Encuentra todos los primos aislados menores que 100.
d) Dos números primos son primos primos si se diferencian en cuatro unidades. Encuentra todas las pareja de primos primos menores que 100.
e) Encuentra todas las ternas de números impares consecutivos y menores que 100, que son primos.
f) Tres números primos son primos trillizos si la diferencia entre el mayor y el menor es seis unidades. Encuentra todas las ternas de primos trillizos menores que 100.
Calendario Matemático SEMCV «Al Khwarizmi». 2025-26. Noviembre
La Sociedad de Educación Matemática de la Comunidad Valenciana «Al Khwarizmi» publica la tercera página de su Calendario Matemático anual, correspondiente al mes de noviembre del curso 2025-26. Los problemas de los días 21-22 y 24-25 corresponden a actividades de este blog.
Se puede acceder a la publicación haciendo «click» sobre la imagen siguiente.
Triángulo y cuadrado
A partir de un triángulo equilátero cualquiera, construir, con regla y compás, un cuadrado de igual área que el triángulo.
Más que cuadrados perfectos III
a) Calcula todos los números «abcd» de cuatro cifras, de forma que los números a, b, c, d y abcd sean cuadrados perfectos.
b) Calcula todos los números «abcd» de cuatro cifras, de forma que los números a, bcd y abcd sean cuadrados perfectos.
c) Calcula todos los números «abcd» de cuatro cifras, de forma que los números abc, d y abcd sean cuadrados perfectos.
d) Calcula todos los números «abcd» de cuatro cifras, de forma que los números ab, cd y abcd sean cuadrados perfectos.
e) Calcula todos los números «abcd» de cuatro cifras, de forma que los números a, bc, d y abcd sean cuadrados perfectos.
