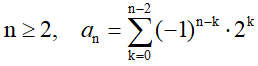La sucesión de Jacobsthal, debida al matemático alemán Ernst Jacobstal (1882-1965), es la siguiente sucesión de números:
0, 1, 1 , 3, 5, 11, 21, 43, 85, 171, 341, 683, 1365, 2731, 5461, . . .
• Esta sucesión se puede obtener como una sucesión recurrente conociendo los dos términos anteriores:
a1 = 0 , a2 = 1 , an = 2·an–2 + an–1
| a3=2a1+a2=0+1=1 |
a4=2a2+a3=2+1=3 |
a5=2a3+a4=2+3=5 |
a6=2a4+a5=6+5=11 |
| a7=2a5+a6=10+11=21 |
a8=2a6+a7=22+21=43 |
a9=2a7+a8=42+43=85 |
a10=2a8+a9=86+85=171 |
• Esta sucesión se puede obtener también como una sucesión recurrente conociendo el término anterior:
a1 = 0 , an = 2·an–1 +(-1)n
| a2=2a1+(-1)2=0+1=1 |
a3=2a2+(-1)3=2–1=1 |
a4=2a3+(-1)4=2+1=3 |
a5=2a4+(-1)5=6–1=5 |
| a6=2a5+(-1)6=10+1=11 |
a7=2a6+(-1)7=22–1=21 |
a8=2a7+(-1)8=42+1=43 |
a9=2a8+(-1)9=86–1=85 |
• También se puede obtener cualquier término de la sucesión sin necesidad de conocer ninguno de los términos anteriores, mediante el término general:
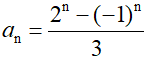
| a0=(1–1)/3=0 |
a1=(2+1)/3=1 |
a2=(4–1)/3=1 |
a3=(8+1)/3=3 |
| a4=(16–1)/3=5 |
a5=(32+1)/3=11 |
a6=(64–1)/3=21 |
a7=(128+1)/3=43 |
• Y otra forma de obtener los términos de esta sucesión, excepto el primero de ellos, es como sumas y diferencias alternas de potencias de 2:
| n=1 → a1 = 0 |
| n=2 → a2 = 20 = 1 |
| n=3 → a3 = 21 – 20 = 2 – 1 = 1 |
| n=4 → a4 = 22 – 21 + 20 = 4 – 2 + 1 = 3 |
| n=5 → a5 = 23 – 22 + 21 – 20 = 8 – 4 + 2 – 1 = 5 |
| n=6 → a6 = 24 – 23 + 22 – 21 + 20 = 16 – 8 + 4 – 2 + 1 = 11 |
| n=7 → a7 = 25 – 24 + 23 – 22 + 21 – 20 = 32 – 16 + 8 – 4 + 2 – 1 = 21 |
Esta relación se puede expresar de la forma: