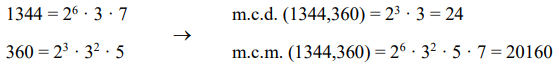Euclides (325-265 a.C.), en el séptimo libro de sus Elementos, describe el siguiente procedimiento para el cálculo del máximo común divisor, m.c.d., de dos números, conocido como Algoritmo de Euclides.

Se empieza dividiendo el número mayor entre el menor. Si se obtiene de resto 0, entonces el número menor es el m.c.d. de ambos. 

Si no se obtiene de resto 0, se divide el divisor de la división anterior entre el resto obtenido y se repite el mismo razonamiento hasta obtener una división exacta. 

Una vez que hayamos obtenido una división exacta, el divisor de la última división es el máximo común divisor de los dos números iniciales.

Ejemplo. Vamos a calcular el m.c.d. de los números 1344 y 360.

Se realizan las divisiones descritas anteriormente hasta obtener una división exacta:

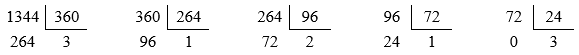
El m.c.d. es el divisor de la última división:

m.c.d.(1344,360) = 24.

El mínimo común múltiplo se puede calcular con la relación:

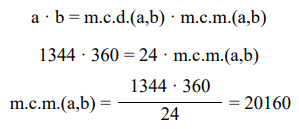
Al calcular el m.c.d. y el m.c.m. con la descomposición factorial de los números, se obtiene: