Curvas algebraicas

Su nombre se debe al astrónomo italiano Giovanni Cassini (1625-1712).

La óvalos de Cassini son el lugar geométrico de los puntos del plano, P, cuyo producto de distancias a dos puntos fijos, F:(a,0) y F’:(-a,0), llamados focos es constante e igual a b².

Si se  define la excentricidad como e=b/a, se verifica que:

• Si e<1, se obtienen dos óvalos simétricos.

• Si e=1, se obtiene la Lemniscata de Bernouili.

• Si e>1, se obtiene una curva cerrada.

Haz «click» sobre la imagen para abrir la construcción de GeoGebra.

La concoide de Nicomedes (siglo III a.C.) es una curva algebraica generada de la siguiente forma:

• Se dibuja una recta r y un punto O que no pertenece a ella.

• Por el punto O se traza una recta cualquiera que corta a la recta r en el punto P.

• Se dibuja una circunferencia de centro P y radio una longitud cualquiera.

• La recta que pasa por O y P corta a esta circunferencia en dos puntos, Q₁ y Q₂.

• Al desplazar el punto P por la recta, los puntos Q₁ y Q₂ describen la concoide.

Haz «click» sobre la imagen para abrir la construcción de GeoGebra.

La hipotrocoide es la curva que recorre un punto fijo, interior, exterior o que pertenece a una circunferencia, cuando dicha circunferencia rueda por el interior de otra circunferencia. 

Si el punto es interior a la circunferencia se obtiene una hipocicloide acortada.

Si el punto pertenece a la circunferencia se obtiene una hipocicloide.

Si el punto es exterior a la circunferencia se obtiene una hipocicloide alargada.

Haz «click» sobre la imagen para abrir la construcción de GeoGebra.

La hipocicloide es la curva que recorre un punto de una circunferencia cuando dicha circunferencia rueda por el interior de otra circunferencia.

Haz «click» sobre la imagen para abrir la construcción de GeoGebra.

La hipocicloide también se puede representar a partir de sus ecuaciones paramétricas.

Si el cociente entre r₁ y r₂ es un número entero se obtiene la hipocicloide construida en la entrada anterior para el valor de n igual al cociente de los radios.

Si el cociente es un número racional, la circunferencia interior tiene que dar más de una vuelta sobre la otra para construir la hipocicloide.

Haz «click» sobre la imagen para abrir la construcción de GeoGebra.

La cisoide de Diocles (240 a.C. – 180 a.C.) es una curva algebraica generada de la siguiente forma:

• Se traza una circunferencia y se representa un diámetro, OP.

• Por uno de los extremos del diámetro, P, se traza la tangente a la circunferencia y se escoge un punto, T, de dicha tangente.

• Se traza la semirrecta con origen en el otro extremo del diámetro, O, que pasa por el punto P. 

• Se traza una circunferencia con centro en O y radio PT.

• La intersección de esta circunferencia con la semirrecta es el punto Q, que verifica d(O,Q)=d(P,T).

• Al desplazar el punto T por la tangente, el punto Q describe la cisoide.

Haz «click» sobre la imagen para abrir la construcción de GeoGebra.

La epitrocoide es la curva que recorre un punto fijo, interior, exterior o que pertenece a una circunferencia, cuando dicha circunferencia rueda por el exterior de otra circunferencia. 

Si el punto es interior a la circunferencia se obtiene una epicicloide acortada.

Si el punto pertenece a la circunferencia se obtiene una epicicloide.

Si el punto es exterior a la circunferencia se obtiene una epicicloide alargada.

Haz «click» sobre la imagen para abrir la construcción de GeoGebra.

La epicicloide es la curva que recorre un punto de una circunferencia cuando dicha circunferencia rueda por el exterior de otra circunferencia.

Haz «click» sobre la imagen para abrir la construcción de GeoGebra.

La epicicloide también se puede representar a partir de sus ecuaciones paramétricas.

Si el cociente entre r₁ y r₂ es un número entero se obtiene la epicicloide construida en la entrada anterior para el valor de n igual al cociente de los radios.

Si el cociente es un número racional, la circunferencia exterior tiene que dar más de una vuelta sobre la otra para construir la epicicloide.

Haz «click» sobre la imagen para abrir la construcción de GeoGebra.

La estrafoide es una curva algebraica generada de la siguiente forma:

• Se trazan dos rectas secantes y sea O el punto de intersección.

• Se representa un punto cualquiera P en alguna de las rectas, que será un punto fijo en la construcción.

• Por el punto P se traza una recta, determinada por los puntos P y Q, que corta a la otra recta inicial en un punto C. 

• Se traza una circunferencia con centro en C y radio OC.

• La recta que pasa por P y Q corta a la circunferencia en los puntos P1 y P2.

• Al modificar la recta (moviendo el punto Q) los puntos P1 y P2 describen la estrafoide.

• Si las rectas iniciales no son perpendiculares, la curva que se obtiene es una estrafoide oblicua.

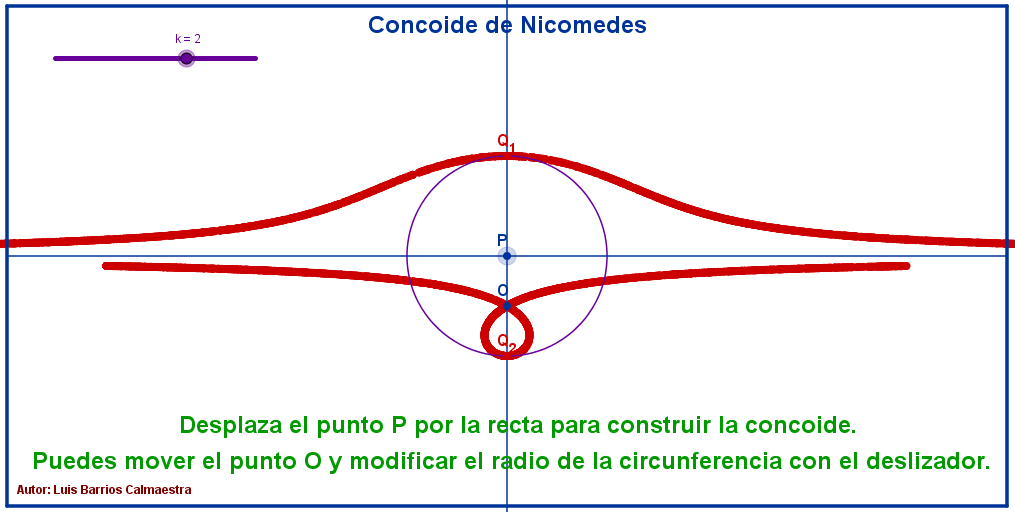
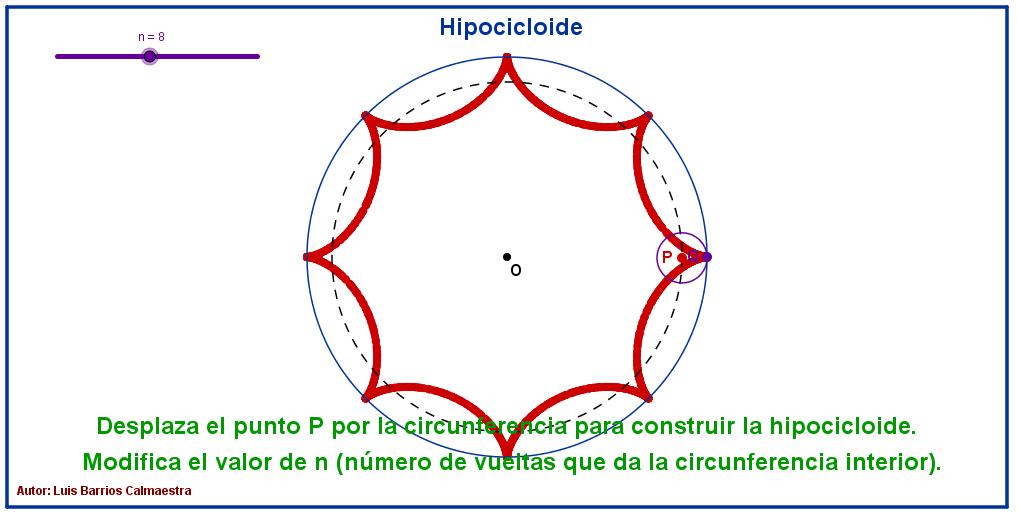
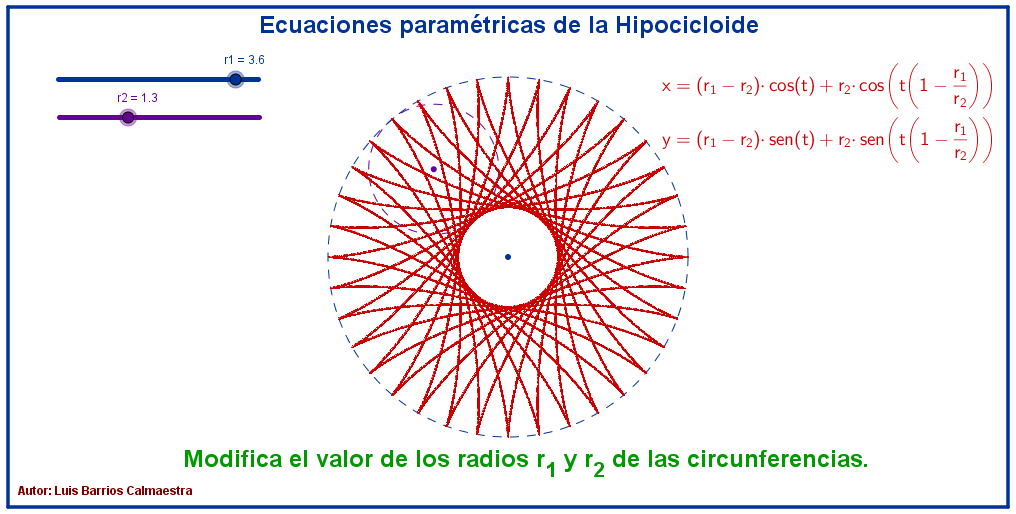
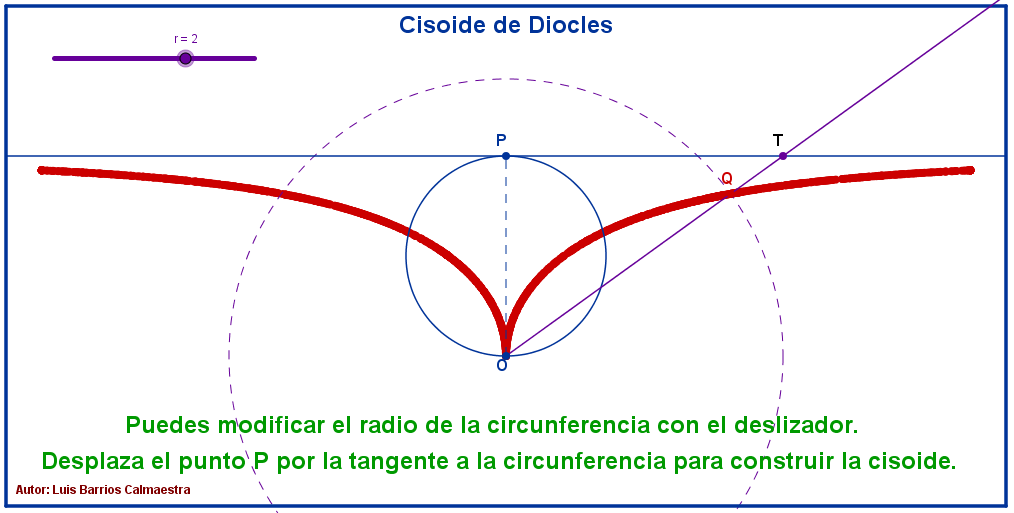
Haz «click» sobre la imagen para abrir la construcción de GeoGebra.