Trocoide
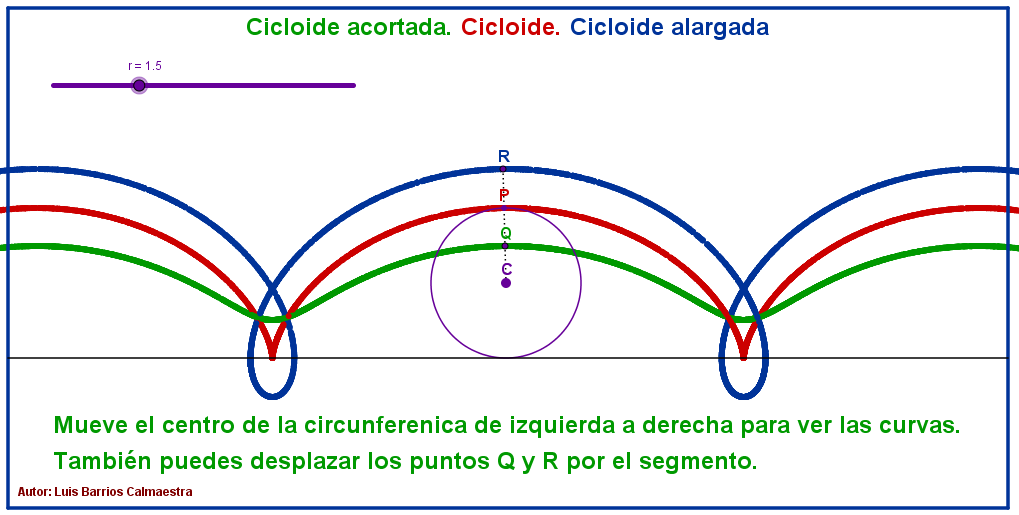
La trocoide es la curva que recorre un punto fijo, interior, exterior o que pertenece a una circunferencia, cuando dicha circunferencia rueda por una línea recta.
Si el punto es interior a la circunferencia se obtiene una cicloide acortada.
Si el punto pertenece a la circunferencia se obtiene una cicloide.
Si el punto es exterior a la circunferencia se obtiene una cicloide alargada.
Haz «click» sobre la imagen para abrir la construcción de Geogebra.