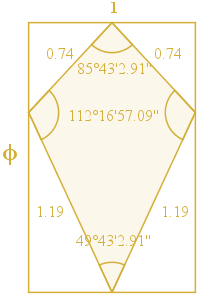
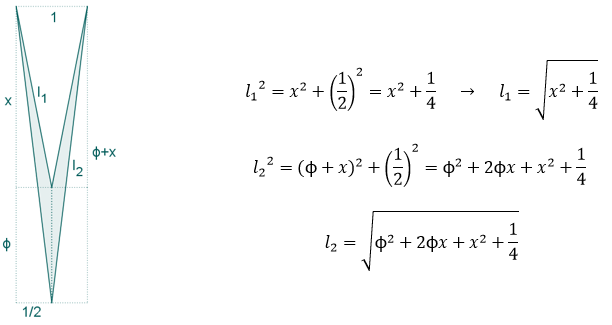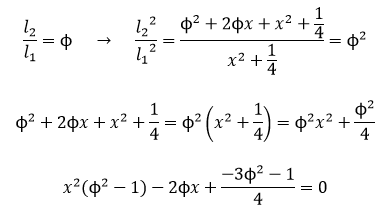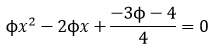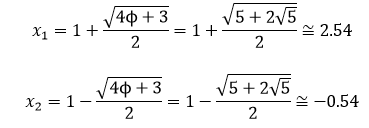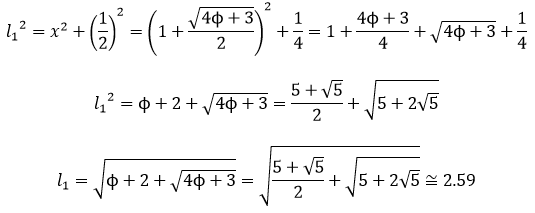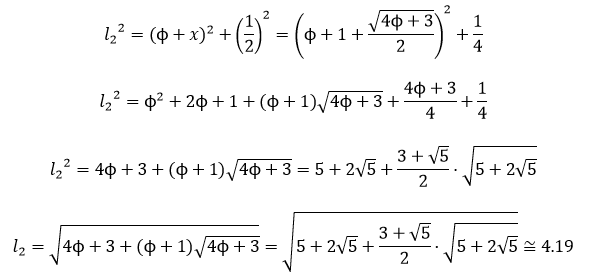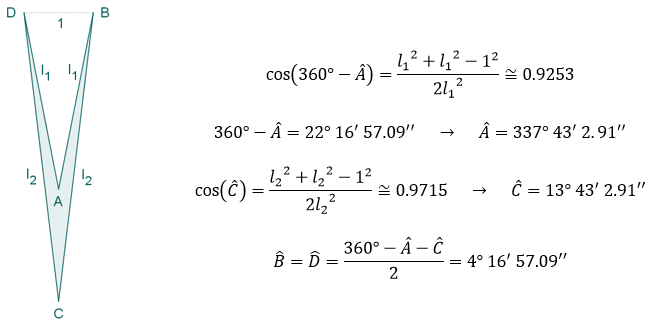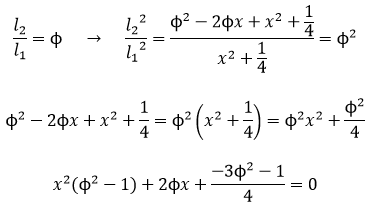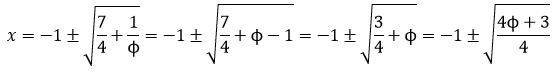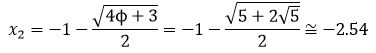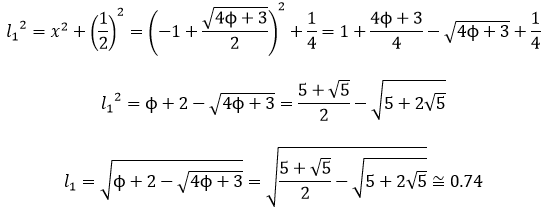Deltoides con proporciones áureas
Publicación del libro digital interactivo «Deltoides con proporciones áureas«, dentro del proyecto iCartesiLibri de la Red Educativa Digital Descartes.
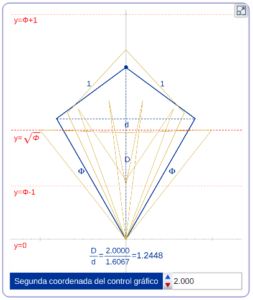
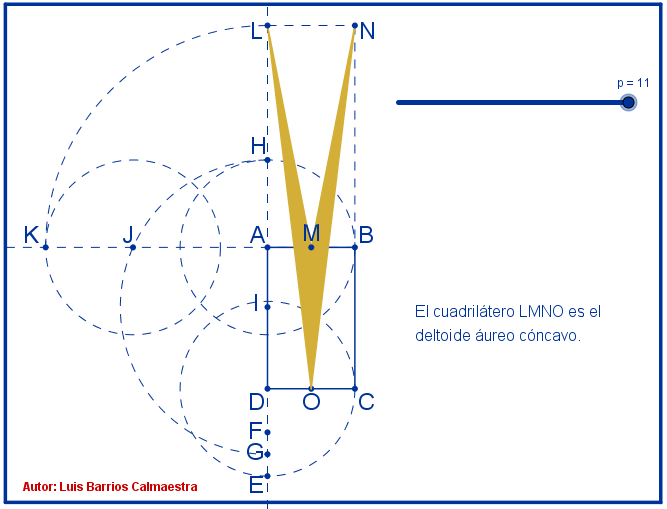
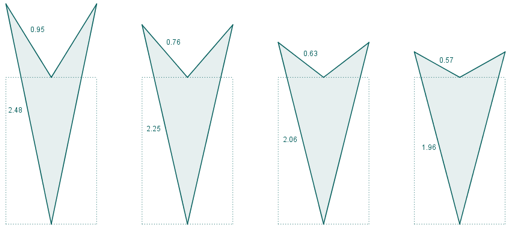
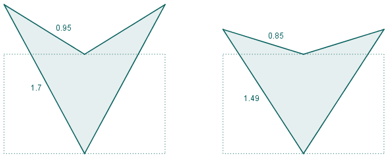
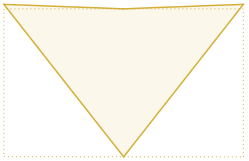
En este libro se estudia la existencia y construcción de deltoides con proporciones áureas. Se estudian deltoides convexos y cóncavos inscritos en un rectángulo áureo. Y se estudia también la existencia de deltoides que, aunque no están inscritos en un rectángulo de oro, verifican que sus lados y sus diagonales están en proporción áurea.
Se incluyen escenas interactivas del Proyecto Descartes que ayudan a realizar la construcción paso a paso de las figuras estudiadas y a una mejor comprensión de sus propiedades.