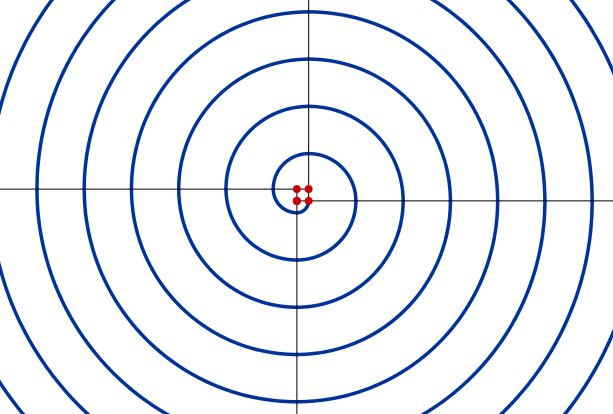
Espiral pentagonal
A partir de los vértices de un pentágono (centros) se dibuja un arco de circunferencia de 72º de amplitud, con centro en uno de ellos y radio la longitud del lado del pentágono. Posteriormente se continúa trazando arcos de 72º rotando los centros y utilizando el punto final del último arco como inicio del siguiente.
Haz «click» sobre la imagen para abrir la construcción de Geogebra.