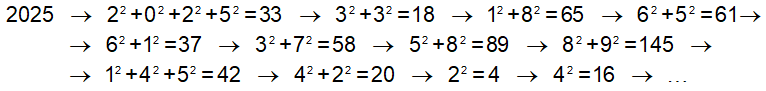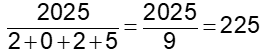Fechas

Hoy, jueves 27 de marzo de 2025, se verifica que el producto de los números del día, el mes y las dos últimas cifras del año, es igual al año actual expresado con cuatro cifras:

27/03/25 → 27×03×25=2025

Además, en veinte instantes de este día, se verifica también que el producto de los números de la hora, los minutos y los segundos, coincide con el año en el que estamos.

El primero de estos instantes es el que aparece en la imagen inicial:

01:45:45 → 01×45×45=2025

Y estos son todos los instantes matemáticos de este día: 

Estos veinte instantes suceden todos los días del año, pero solamente habrá un día más en el que se verifique que el producto de los números del día, el mes y las dos últimas cifras del año, es igual al año actual expresado con cuatro cifras.

¡ FELIZ 2025 !

2025 = 45² = ( 20 + 25 ) ²

2025 = ( 21 + 24 ) · ( 22 + 23 )

PROPIEDADES DEL NÚMERO 2025

• Descomposición factorial:     2025 = 3⁴ × 5²

• Número de divisores: (4+1)·(2+1) = 15.

1, 3, 5, 9, 15, 25, 27, 45, 75, 81, 135, 225, 405, 675 y 2025

• Suma de sus cifras:     2 + 0 + 2 + 5 = 9

• Suma de los cuadrados de sus cifras:    2² + 0² + 2² + 5² = 33

• El número 2025 se puede obtener como el cuadrado de la suma de los nueve primeros números naturales:   

( 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 ) ² = 2025

• El número 2025 se puede obtener como suma de los cubos de los nueve primeros números naturales:   

1³ + 2³ + 3³ + 4³ + 5³ + 6³ + 7³ + 8³ + 9³ = 2025

• El número 2025 se puede obtener sumando y restando los cubos de los siguientes números impares consecutivos:  

15³ – 13³ + 11³ – 9³ + 7³ – 5³ + 3³ = 2025 

ACTIVIDADES CON EL NÚMERO 2025

Las siguientes actividades se proponen para números desde una hasta cuatro cifras. Como ayuda para resolverlas, si el número tiene menos de cuatro cifras se puede completar añadiendo ceros a la izquierda.

• El número 2025 se escribe uniendo dos múltiplos de 5 consecutivos, 20 y 25. ¿Cuáles fueron los tres años anteriores a 2025 con esta propiedad? ¿Cuáles serán los cinco años siguientes con esta propiedad? ¿Cada cuántos años sucede esto? ¿Por qué?

• La suma de las cifras del número 2025 es 9. ¿Cuáles fueron los cinco años anteriores a 2025 con esta propiedad? ¿Cuáles serán los cinco años siguientes con esta propiedad?

• La suma de los cuadrados de las cifras del número 2025 es 33. ¿Cuáles fueron los cinco años anteriores a 2025 con esta propiedad? ¿Cuáles serán los cinco años siguientes con esta propiedad?

• El número 2025 es un cuadrado perfecto 2025=45². ¿Cuál fue el año anterior a 2025 con esta propiedad? ¿Cuál será el año siguiente con esta propiedad? ¿Cuál fue el año anterior que fue un cubo perfecto? ¿Cuál será el año siguiente que sea un cubo perfecto?

• El número 2025 se puede expresar de la forma, 2025=(20+25)². ¿Cuál fue el año anterior a 2025 con esta propiedad (en caso de que el número no tenga cuatro cifras se completa con ceros a la izquierda)? ¿Cuáles serán los dos años siguientes con esta propiedad?

• Se verifica que:

2025=(21+24)·(22+23)       2024=(21+23)·(22+24)       2021=(21+22)·(23+24)

¿Cuáles fueron los cinco años anteriores con una relación similar? ¿Cuáles serán los cinco años siguientes?

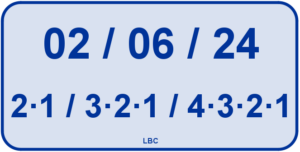
• Escribimos la fecha de un día cualquiera del año con el formato “dd/mm/aa”, es decir, dos cifras para el día del mes, dos cifras para el mes y dos cifras para el año. ¿Qué días del año verifican “dd+mm=aa”? ¿Qué días del año verifican “dd·mm=aa”? ¿Qué días del año verifican “dd·mm·aa=2025”?

• Escribimos la hora, minutos y segundos de un instante de cualquier día del año con el formato “hh:mm:ss”, es decir, dos cifras para la hora, dos cifras para los minutos y dos cifras para los segundos. ¿Qué instantes de cada día verifican “hh·mm·ss=2025”?

• El año 2025 comienza y termina en miércoles. ¿Cuál fue el año anterior que empezó y terminó en miércoles? ¿Cuál será el año siguiente?

Las soluciones de las actividades las puedes encontrar en el siguiente enlace:

https://proyectodescartes.org/miscelanea/materiales_didacticos/Feliz_2025/index.html

OTRAS PROPIEDADES DEL NÚMERO 2025

Según los conjuntos numéricos que se estudian en la enseñanza de las Matemáticas, el número 2025 es un número natural, entero, racional y real. También se puede decir que es impar, múltiplo de 5, compuesto y cuadrado perfecto. En Matemáticas Recreativas aparecen otros tipos de números que verifican algunas propiedades curiosas y que reciben distintas denominaciones, llegando a ser contradictorias en algunos casos.

Según algunas de estas propiedades curiosas, se puede decir que el número 2025:

Es un número deficiente, la suma de sus divisores, excepto el mismo número, es menor que el número:

1+3+5+9+15+25+27+45+75+81+135+225+405+675 = 1726 < 2025

• Sin embargo, es un número poderoso porque es divisible por los cuadrados de cada uno de los factores primos que aparecen en su descomposición factorial.

Los factores primos que aparecen en la descomposición factorial de 2025 son 3 y 5. El número 2025 también es divisible por 3² y 5².

• Es un número infeliz, no se obtiene 1 al final de la secuencia de operaciones:

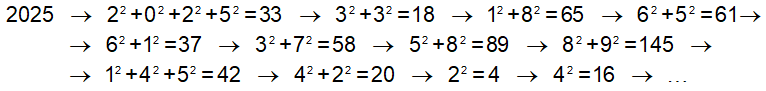
• Sin embargo, es un número que transmite alegría o número de Harshad, porque es divisible por la suma de sus cifras:

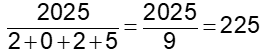
Pero, independientemente de lo que digan las Matemáticas de este número,

¡ Feliz 2025 !

El día de hoy, domingo 2 de junio de 2024, es una fecha matemáticamente muy curiosa.

Con notación matemática:

Hoy es sábado 30 de marzo (30/03) de 2024. Hoy es el día 90º (nonagésimo) de un año bisiesto. Un día interesante matemáticamente porque:

30 × 3 = 90

En el día de hoy, 8 de noviembre de 2023, se produce este momento curioso que nos recuerda el año actual y nos indica el próximo año.

Este hecho se vuelve a repetir en otros dos momentos del día.

Esta situación ya se produjo también los días 22 de abril y 11 de agosto de este mismo año.