Un camino es simple si no repite vértices. Un camino simple que contiene todos los vértices del grafo es un  camino hamiltoniano.

Un ciclo es un camino cerrado en el que los únicos vértices repetidos son el primero y el último. 

Un grafo hamiltoniano es un grafo que contiene un ciclo hamiltoniano. 

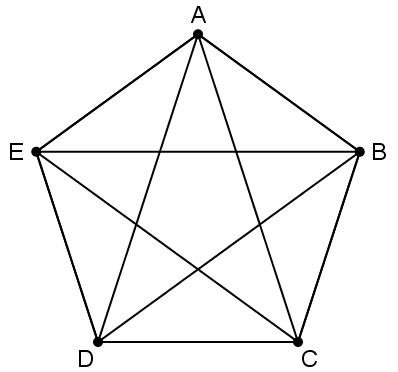
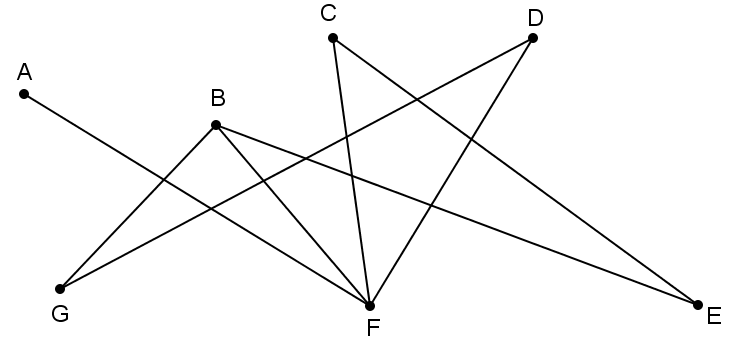
En el grafo siguiente, un camino hamiltoniano es el formado por las aristas AF, FC, CE, EB, BG, GD. Sin embargo, no existe un ciclo hamiltoniano. Por tanto, no es un grafo hamiltoniano.

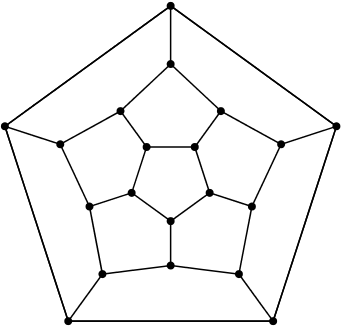
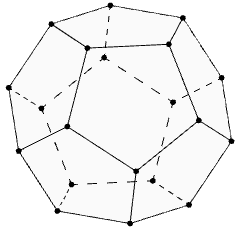
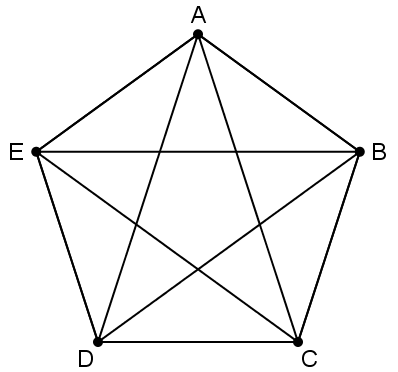
El grafo siguiente, que se obtiene a partir del dodecaedro del viajero, si contiene un  ciclo hamiltoniano, que tienes que encontrar como solución al problema. Por tanto, este grafo sí es un grafo hamiltoniano.

El matemático irlandés William Rowan Hamilton (1805-1865)  inventó este juego conocido como el dodecaedro del viajero o viaje alrededor del mundo. Supongamos que en un dodecaedro, cada uno de los veinte vértices representa una ciudad del mundo. El juego consiste en realizar un recorrido partiendo de una de las ciudades y, siguiendo las aristas del dodecaedro, pasar por todas las ciudades una sola vez, finalizando en la ciudad de inicio.

El recorrido en el dodecaedro es equivalente a encontrar un recorrido con las mismas condiciones en el grafo de la derecha.

Un grafo es conexo si cada par de vértices están unidos por un camino.

Un grafo conexo es euleriano si y solo si cada vértice tiene grado par.

Si un grafo contiene un camino euleriano, entonces todos los vértices tienen grado par o solamente dos vértices tienen grado par. En este caso, para construir el camino euleriano hay que empezar por uno de los vértices de grado impar y acabar en el otro.

En el siguiente grafo, el vértice A tiene grado 1 y el vértice B tiene grado 3. No puede ser un grafo euleriano, pero sí se puede construir un camino euleriano empezando por el vértice A y acabando por el vértice B o al contrario.

En el siguiente grafo todos los vértices tienen grado par, es un grafo euleriano. Se puede construir un circuito euleriano, empezando y acabando en un mismo vértice.

En el problema de los puentes de Königsberg, realizar el recorrido propuesto, equivale a construir la siguiente figura sin levantar el lápiz del papel y sin pasar dos veces por la misma línea, es decir, construir un circuito euleriano. Pero no se puede construir este camino porque los cuatro vértices del grafo tienen grado impar, por tanto, no es posible recorrer la ciudad a pie, pasando una sola vez por cada uno de los puentes y volviendo al punto inicial.

Utiliza estos resultados para resolver la siguiente actividad propuesta en este blog con anterioridad:

Sin levantar el lápiz del papel

Un camino en un grafo es un conjunto de aristas consecutivas que unen dos vértices. Un camino es cerrado si los dos vértices extremos coinciden. Un circuito es un camino cerrado que no contiene aristas repetidas.

En el grafo anterior, un camino que une los puntos A y E es el formado por las aristas AF, FC, CE.

Un circuito que sale que parte de G y llega a G es el formado por las aristas GD, DF, FC, CE, EB, BG.

Un camino euleriano es un camino que contiene todas las aristas sin repetir ninguna. En el grafo anterior, el camino AF, FB, BE, EC, CF, FD, DG, GB es un camino euleriano.

Un grafo euleriano es un grafo que contiene un circuito euleriano. El grafo anterior no contiene ningún circuito euleriano. El grafo siguiente contiene el circuito euleriano: AB, BC, CD, DE, EA, AC, CE, EB, BD, DA. Es por tanto, un grafo euleriano.

Un grafo es un conjunto de puntos en el plano o en el espacio, llamados vértices, conectados por un conjunto de líneas, llamadas aristas. 

Se llama grado de un vértice al número de aristas que tienen por extremo dicho vértice. En el grafo anterior el vértice F tienen grado 4, el vértice B tiene grado3, los vértices C, D, E y G tienen grado 2 y el vértice A tiene grado 1.

Un grafo en el que todos los vértices tienen el mismo grado, se llama regular.

Si en un grafo existen varias aristas entre los mismos vértices, se llama multigrafo. Si existe al menos una arista, llamada lazo, cuyos extremos coinciden, el grafo se llama pseudografo.

Königsberg era una ciudad de Prusia Oriental. Actualmente es la ciudad rusa de Kaliningrado. Está atravesada por el río Pregolya, que se bifurca en dos brazos dejando la isla de Kneiphof entre ellos.

En el siglo XVIII había siete puentes, aproximadamente como se puede observar en la figura. En esa época se planteó la situación de si era posible recorrer la ciudad a pie, pasando una sola vez por cada uno de los puentes y volviendo al punto inicial. Esta situación se extendió como juego y, posteriormente, como problema matemático.

El matemático suizo Leonhard Euler (1707-1783) resolvió el problema en 1736, dando origen con la solución a la Teoría de Grafos.

Si se representan con los puntos azules las regiones de tierra firme separadas por el río, cada puente une dos puntos azules, existiendo siete caminos posibles que unen cuatro puntos, representados en color naranja en la imagen derecha.

Hacer el recorrido propuesto, equivale a construir la siguiente figura sin levantar el lápiz del papel y sin pasar dos veces por la misma línea. 

Euler resolvió el problema de los puentes de Königsberg demostrando que no es posible realizar dicho recorrido.