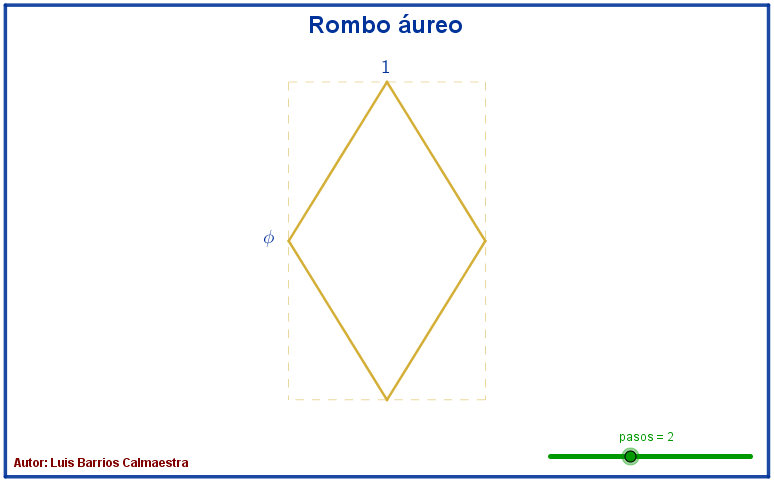
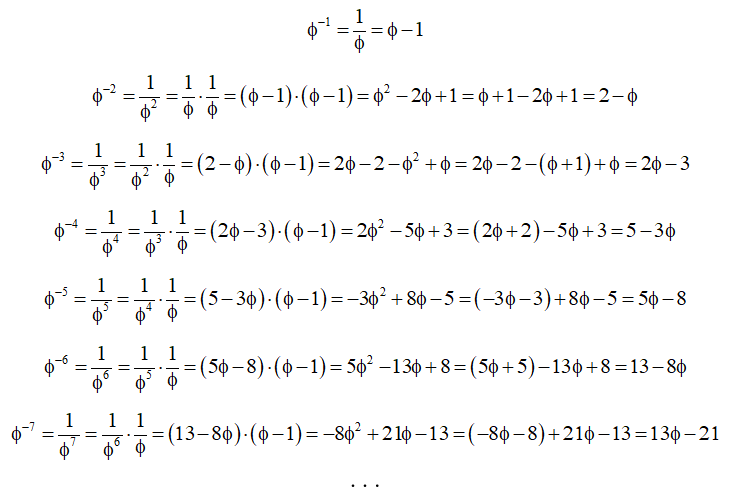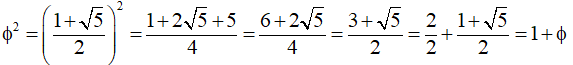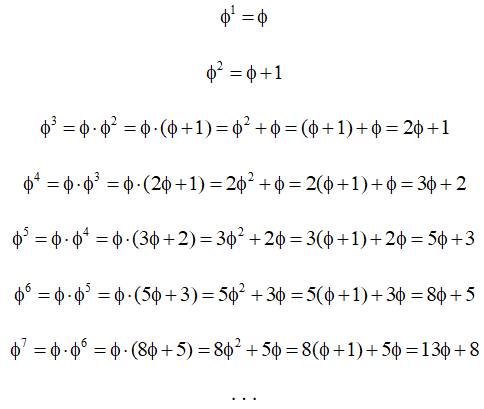Un segmento de longitud áurea
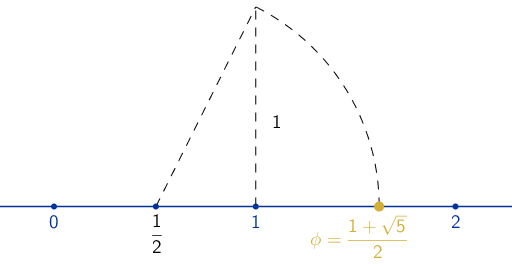
El número de oro es un número algebraico. Esto significa que se puede obtener como solución de una ecuación polinómica con coeficientes racionales. También que se puede representar gráficamente con regla y compás. La representación gráfica más conocida y más fácil se deduce a partir de su expresión numérica con fracciones y raíces. Se muestra en la siguiente figura:
Otros segmentos cuya longitud es el número de oro son:
• La diagonal de un pentágono regular de lado una unidad.
• El radio de la circunferencia circunscrita a un decágono regular de lado una unidad.
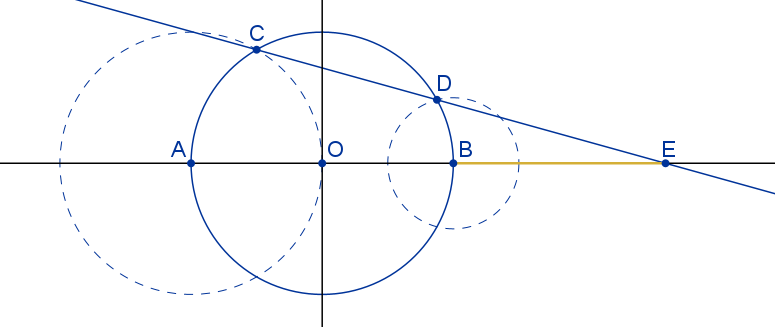
Con el siguiente procedimiento se puede construir gráficamente, con regla y compás, otro segmento cuya longitud es el número de oro.
Haciendo «click» sobre la imagen se puede seguir la construcción paso a paso en una miscelánea del Proyecto Descartes.
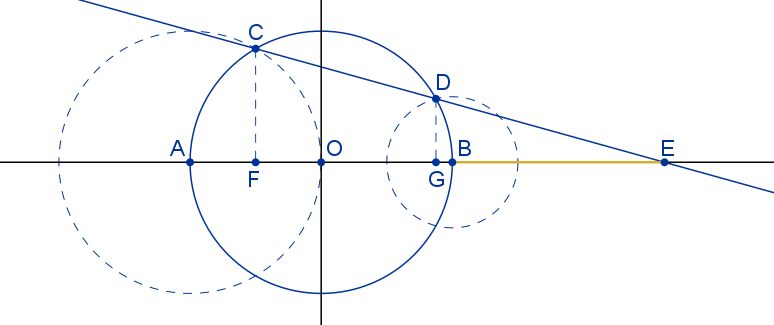
1. Se representa una circunferencia con centro el origen de coordenadas y una unidad de radio.
2. Sean A y B los puntos de corte de la circunferencia con el eje de abscisas.
3. Con centro el punto A se traza una circunferencia de radio 1 que corta a la circunferencia inicial en dos puntos. Elegimos uno de ellos, por ejemplo C.
4. Con centro el punto B se traza una circunferencia de radio 1/2 que corta a la circunferencia inicial en dos puntos. Elegimos uno de ellos, por ejemplo D.
5. Se traza la recta que pasa por los puntos C y D. Esta recta corta al eje de abscisas en el punto E.
6. La longitud del segmento BE coincide con el número de oro.
Demostración.
Ecuación de la circunferencia de centro O y radio 1:
![]()
Ecuación de la circunferencia de centro A:(-1,0) y radio 1:
![]()
Ecuación de la circunferencia de centro B:(1,0) y radio 1/2:
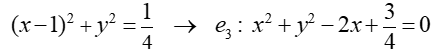
Coordenadas del punto C. Se pueden calcular resolviendo el sistema de ecuaciones formado por las ecuaciones de las dos circunferencias a las que pertenece.
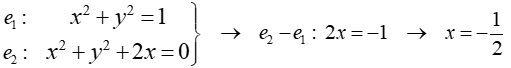
Sustituyendo el valor de x en la primera ecuación, se obtiene:
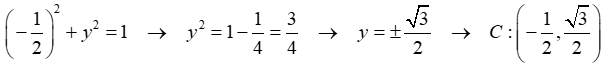
Coordenadas del punto D. Se pueden calcular resolviendo el sistema de ecuaciones formado por las ecuaciones de las dos circunferencias a las que pertenece.

Sustituyendo el valor de x en la primera ecuación, se obtiene:
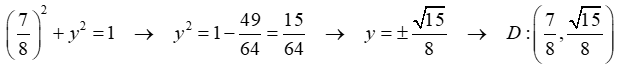
Se representan ahora las proyecciones de los puntos C y D sobre el eje de abscisas obteniendo los puntos F y G respectivamente.
Los triángulos CFE y DGE son semejantes. Aplicando el Teorema de Thales:
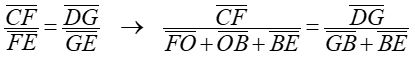
Las longitudes de los segmentos son:
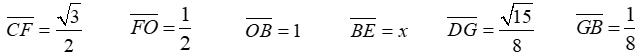
Sustituyendo estos valores en la expresión anterior se puede calcular la longitud del segmento BE:
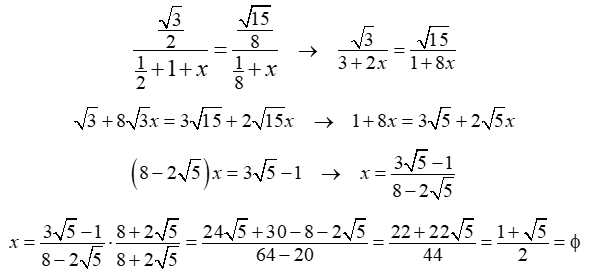
Si en la construcción gráfica realizada, la circunferencia inicial se construye con centro el punto (-1,0), en lugar del origen de coordenadas, el punto E coincide en el eje de abscisas con la representación del número de oro en la recta real.