El matemático inglés John Wallis (1616-1703), obtiene en 1665, a partir de otro producto infinito, las 100 primeras cifras decimales del número π:
Utilizando el emulador de la calculadora Classwiz fx-570SP X Iberia, podemos obtener el valor del producto para 1000, 10000, 100000 y 1000000 de factores:
El matemático francés François Viète (1540-1603) calculó 10 decimales exactos de π utilizando un polígono de 393216 lados.
En 1593 descubre el primer producto infinito cuyo producto es una expresión de π, obteniendo con él 9 cifras decimales.
Utilizando todas las memorias de la calculadora Classwiz fx-570SP X Iberia, podemos obtener desde el segundo hasta el noveno factor, de los infinitos que tiene el producto:
La aproximación que se obtiene multiplicando solamente el primer factor, 2, y los nueve factores anteriores es:
Al multiplicar los infinitos factores se obtiene el número π.
• En la India, Aryabhata, entre los siglos V y VI, utilizaba 3.1416.
• Brahmagupta, matemático indio, en el siglo VI utiliza 
• El matemático árabe Al Jwarizmi, en el siglo IX, indica en su obra «Álgebra», que el hombre práctico usa como valor de π, 22/7, el geómetra utiliza 3 y el astrónomo 3.1416.
• Madhava, matemático indio, en el año 1400 utiliza el desarrollo en serie de la arcotangente y suma 21 términos de la serie para calcular 11 cifras decimales. Esta serie la redescubriría doscientos años después Gregory.
• En 1429, Al-Khasi, matemático persa, obtiene 16 decimales utilizando el método de Arquímedes con polígonos de un elevado número de lados.
• El matemático alemán Ludolf Van Ceulen hizo una primera aproximación con 20 cifras decimales y después llegó a calcular 35 cifras decimales de π, utilizando el método de Arquímedes y un polígono de 262 lados.
El número π es un número trascendente, esto significa que no se puede representar con regla y compás. Sin embargo, algunos matemáticos han intentado conseguir alguna aproximación gráfica. El matemático chino Zu Chongzhi (429-500), obtiene la aproximación más precisa durante los 900 años posteriores.
Haz «click» sobre la imagen para abrir la construcción con GeoGebra y seguirla paso a paso.
Aplicando el Teorema de Pitágoras:
Los triángulos AOB y CDB son semejantes, por tanto:
Los triángulos ADB y CEB son semejantes, por tanto:
Si se añade este segmento a un segmento de longitud tres, tendríamos un segmento de longitud π:
El método de Arquímedes fue utilizado por matemáticos posteriores, aumentando el número de lados de los polígonos, para obtener mejores aproximaciones.
• Ptolomeo, (110-118), utiliza polígonos de hasta 720 lados y obtiene la aproximación:
• En China, Liu Hui en el siglo III, utilizó polígonos de hasta 3072 lados para obtener el valor de π con cinco cifras decimales: 3’14159.
El matemático griego Arquímedes, (287 a.C.-212 a.C.), fue el primero en idear un procedimiento matemático para calcular el valor de π, obteniendo que estaba comprendido entre 3+10/71=223/71 y 3+1/7=22/7.
El método usado por Arquímedes consistía en circunscribir e inscribir polígonos regulares de n lados en circunferencias y calcular el perímetro de dichos polígonos. Empezó con hexágonos circunscritos e inscritos, y fue doblando el número de lados hasta llegar a polígonos de 96 lados.
(Haciendo «click» con el ratón sobre cualquiera de las imágenes se puede abrir una miscelánea de la Red Educativa Digital Descartes, en la que se puede comprobar de forma interactiva, modificando los parámetros de las pestañas de la barra inferior, como varía el cociente entre el perímetro del polígono regular y el diámetro de la circunferencia, en los polígonos inscritos y circunscritos, por separado o de forma conjunta).
Con los instrumentos de cálculo actuales la acotación sería:
• En el Papiro de Rhind, (papiro egipcio, de 6 m. de longitud y 32 cm. de ancho, escrito por el escriba Ahmes a mediados del siglo XVI a.C., copiado de un documento del siglo XIX a.C.), se dan instrucciones para calcular el área de un círculo “Corta 1/9 del diámetro y construye un cuadrado sobre la longitud restante. Este cuadrado tiene igual área que el circulo”. Se puede deducir que el valor de π es 256/81, aproximadamente 3’16.
• En Babilonia, aproximadamente en 1600 a. C., medían la circunferencia de un círculo como tres veces el diámetro y el área como un doceavo del cuadrado de la circunferencia, lo cual es correcto para una estimación de π a 3.
• En la Tablilla de Susa, (tablilla con problemas de Geometría del segundo milenio antes de Cristo, aproximadamente del año 1600 a. C.), en Mesopotamia, los babilonios utilizaban como valor de π, 3+1/8=3’125.
• En la Biblia, (libro primero de los Reyes, capítulo 7, versículo 23 y en el libro segundo de las Crónicas, capítulo 4, versículo 2), se puede leer la descripción de un depósito de agua para el palacio del Rey Salomón: «Hizo fundir asimismo un mar de diez codos de un lado al otro, perfectamente redondo. Tenía cinco codos de altura y a su alrededor un cordón de treinta codos«. De aquí se deduce que se da a π el valor 3.
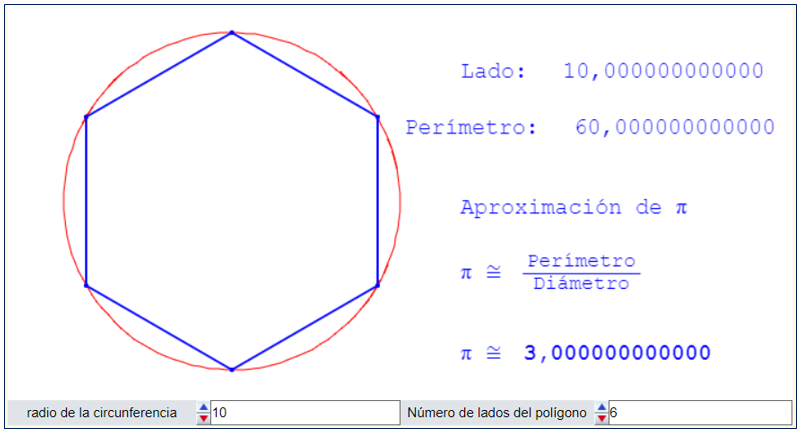
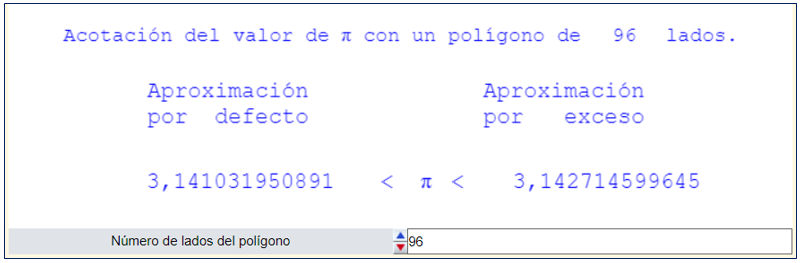
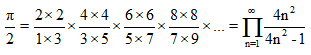Al dividir la longitud de cualquier circunferencia entre su diámetro se obtiene siempre el mismo número, que se representa por π. (Haz «click» sobre la imagen)
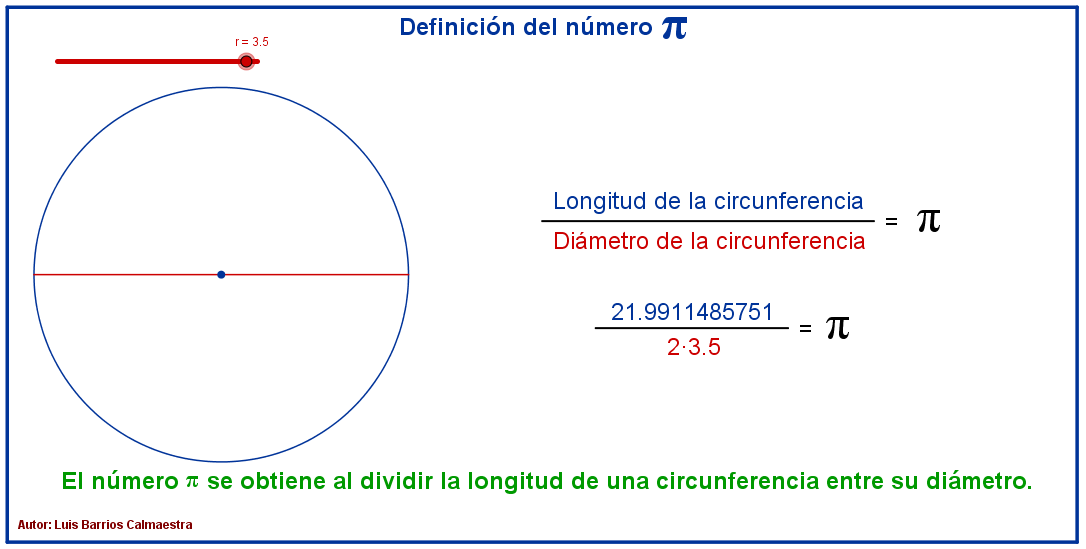
Desde el siglo XIX a. C. en el que se conoce una primera aproximación, hasta el siglo XXI actual con el cálculo de billones de cifras decimales con potentes ordenadores, pasando por el momento en el que se adopta el símbolo con el que lo conocemos, el número π ha sido estudiado por distintas civilizaciones y matemáticos de todas las épocas.
El símbolo π lo utilizó por primera vez William Oughtred (1574-1660) como inicial de «peripheria» (perímetro), utilizando la letra correspondiente del alfabeto griego. Posteriormente lo propuso para su utilización William Jones en 1706. Pero fue el matemático suizo Leonhard Euler, en 1737, al utilizarlo en su libro “Introductio in Analysin Infinitorum” el que extendió su uso.
El matemático alemán Johan Heinrich Lambert, en 1766, demostró que π es un número irracional, es decir, que tiene infinitas cifras decimales no periódicas. Hoy en día es fácil calcular el número π con una gran cantidad de cifras decimales utilizando un ordenador.
π=3.14159265358979323846264338327950288419716939937510582097494459230781640628620899862803482534211706798 . . .
Ferdinand Lindemann, en 1882 demostró que π es un número trascendente, es decir, no se puede construir con regla y compás. La longitud de una semicircunferencia de 1 cm de radio es igual a π, pero es imposible representar, con regla y compás, un segmento rectilíneo de longitud π.
Historias de Pi.
La serie “Universo matemático” fue creada por el profesor Antonio Pérez Sanz y producida por RTVE en 2000. Ahora RTVE la pone a disposición de los docentes a través de su menú “a la carta”.
Haz click sobre la imagen inferior para verlo.
