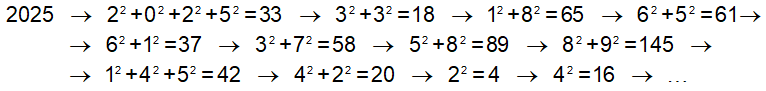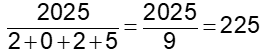Números

¡ FELIZ 2026 !

2026, un número matemáticamente feliz

PROPIEDADES DEL NÚMERO 2026

• Descomposición factorial. 2026 es un número biprimo o semiprimo porque es igual al producto de dos números primos:

2026 = 2 × 1013

• Número de divisores: (1+1)·(1+1) = 2·2 = 4.

div(2026) = { 1 , 2 , 1013 , 2026 }

• Suma de sus cifras:     

2 + 0 + 2 + 6 = 10

• Suma de los cuadrados de sus cifras:   

2² + 0² + 2² + 6² = 44

• Suma de los productos de cada dos cifras consecutivas:   

2 × 0 + 0 × 2 + 2 × 6 = 12

• Operaciones curiosas con resultado 2026:   

ACTIVIDADES CON EL NÚMERO 2026

• El número 2026 no tiene ninguna cifra impar. ¿Cuál fue el año anterior con todas sus cifras impares? ¿Cuántos años tenías? ¿Cuál será el año siguiente con todas sus cifras impares? ¿Cuántos años tendrás?

• El número 2026 se escribe uniendo dos números que se diferencian en seis unidades, 20 y 26. ¿Cuáles fueron los cinco años anteriores a 2026 con esta propiedad? ¿Cuáles serán los cinco años siguientes? ¿Cada cuántos años sucede esto? ¿Por qué?

• La suma de las cifras del número 2026 es 10. ¿Cuáles fueron los cinco años anteriores a 2026 con esta propiedad? ¿Cuáles serán los cinco años siguientes?

• La suma de los cuadrados de las cifras del número 2026 es 44. ¿Cuáles fueron los cinco años anteriores a 2026 con esta propiedad? ¿Cuáles serán los cinco años siguientes?

• La suma de los productos de cada dos cifras consecutivas del número 2026 es 12. ¿Cuáles fueron los cinco años anteriores a 2026 con esta propiedad? ¿Cuáles serán los cinco años siguientes?

• Escribimos la fecha de un día cualquiera del año con el formato “dd/mm/aa”, es decir, dos cifras para el día del mes, dos cifras para el mes y dos cifras para el año. ¿Qué días del año verifican “dd+mm=aa”? ¿Qué días del año verifican “dd·mm=aa”? ¿Qué días del año verifican “dd·mm=2026”?

• Escribimos la hora, minutos y segundos de un instante de cualquier día del año con el formato “hh:mm:ss”, es decir, dos cifras para la hora, dos cifras para los minutos y dos cifras para los segundos. ¿Qué instantes de cada día verifican hh·mm·ss = 26?

• El año 2026 comienza y termina en jueves. ¿Cuál fue el año anterior que empezó y terminó en jueves? ¿Cuál será el año siguiente que empiece y termine en jueves?

OTRAS PROPIEDADES DEL NÚMERO 2026

• Es un número deficiente, la suma de sus divisores, excepto el mismo número, es menor que el número:

1 + 2 + 1013 = 1016 < 2026

• Es un número feliz porque se obtiene 1 al final de la secuencia de operaciones:

• En algunos formatos de fechas se utilizan solamente dos cifras para escribir el año. Así 2026 se escribe como 26, que indica el año número 26 del siglo XXI.

El número 26 es el único número que está comprendido entre un cuadrado perfecto y un cubo perfecto:

5² = 25 < 26 < 27 = 3³

Pero, independientemente de lo que digan las Matemáticas de este número,

¡ Feliz 2026 !

En algunos formatos de escritura de fechas, se escribe el año con las dos últimas cifras. Así el año 2025 se representa por 25, que indica el año número 25 del siglo XXI. Los números con los que se representan este año, tanto de dos cifras como de cuatro cifras, son ambos cuadrados perfectos.

Los meses, cuyos números de orden son cuadrados perfectos, son enero (1²), abril (2²) y septiembre (3²). 

Y los días con números cuadrados perfectos son 1, 4, 9, 16 y 25.

Las siguientes fechas de este año están formadas por tres números cuadrados perfectos.

De todos ellos, el día de hoy, martes 16 de septiembre de 2025, tiene además un interés añadido. Los números que indican la fecha son los cuadrados de la terna pitagórica con los números más pequeños que existe.

Se verifica que:

4² + 3² = 5²  → 16 + 9 = 25

En el día de hoy, 9 de septiembre de 2025, se producen veinte interesantes instantes matemáticos de los cuarenta instantes matemáticos de este año. Uno de ellos es el siguiente:

Y estos son todos los instantes matemáticos de este día: 

Hoy, jueves 27 de marzo de 2025, se verifica que el producto de los números del día, el mes y las dos últimas cifras del año, es igual al año actual expresado con cuatro cifras:

27/03/25 → 27×03×25=2025

Además, en veinte instantes de este día, se verifica también que el producto de los números de la hora, los minutos y los segundos, coincide con el año en el que estamos.

El primero de estos instantes es el que aparece en la imagen inicial:

01:45:45 → 01×45×45=2025

Y estos son todos los instantes matemáticos de este día: 

Estos veinte instantes suceden todos los días del año, pero solamente habrá un día más en el que se verifique que el producto de los números del día, el mes y las dos últimas cifras del año, es igual al año actual expresado con cuatro cifras.

¡ FELIZ 2025 !

2025 = 45² = ( 20 + 25 ) ²

2025 = ( 21 + 24 ) · ( 22 + 23 )

PROPIEDADES DEL NÚMERO 2025

• Descomposición factorial:     2025 = 3⁴ × 5²

• Número de divisores: (4+1)·(2+1) = 15.

1, 3, 5, 9, 15, 25, 27, 45, 75, 81, 135, 225, 405, 675 y 2025

• Suma de sus cifras:     2 + 0 + 2 + 5 = 9

• Suma de los cuadrados de sus cifras:    2² + 0² + 2² + 5² = 33

• El número 2025 se puede obtener como el cuadrado de la suma de los nueve primeros números naturales:   

( 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 ) ² = 2025

• El número 2025 se puede obtener como suma de los cubos de los nueve primeros números naturales:   

1³ + 2³ + 3³ + 4³ + 5³ + 6³ + 7³ + 8³ + 9³ = 2025

• El número 2025 se puede obtener sumando y restando los cubos de los siguientes números impares consecutivos:  

15³ – 13³ + 11³ – 9³ + 7³ – 5³ + 3³ = 2025 

ACTIVIDADES CON EL NÚMERO 2025

Las siguientes actividades se proponen para números desde una hasta cuatro cifras. Como ayuda para resolverlas, si el número tiene menos de cuatro cifras se puede completar añadiendo ceros a la izquierda.

• El número 2025 se escribe uniendo dos múltiplos de 5 consecutivos, 20 y 25. ¿Cuáles fueron los tres años anteriores a 2025 con esta propiedad? ¿Cuáles serán los cinco años siguientes con esta propiedad? ¿Cada cuántos años sucede esto? ¿Por qué?

• La suma de las cifras del número 2025 es 9. ¿Cuáles fueron los cinco años anteriores a 2025 con esta propiedad? ¿Cuáles serán los cinco años siguientes con esta propiedad?

• La suma de los cuadrados de las cifras del número 2025 es 33. ¿Cuáles fueron los cinco años anteriores a 2025 con esta propiedad? ¿Cuáles serán los cinco años siguientes con esta propiedad?

• El número 2025 es un cuadrado perfecto 2025=45². ¿Cuál fue el año anterior a 2025 con esta propiedad? ¿Cuál será el año siguiente con esta propiedad? ¿Cuál fue el año anterior que fue un cubo perfecto? ¿Cuál será el año siguiente que sea un cubo perfecto?

• El número 2025 se puede expresar de la forma, 2025=(20+25)². ¿Cuál fue el año anterior a 2025 con esta propiedad (en caso de que el número no tenga cuatro cifras se completa con ceros a la izquierda)? ¿Cuáles serán los dos años siguientes con esta propiedad?

• Se verifica que:

2025=(21+24)·(22+23)       2024=(21+23)·(22+24)       2021=(21+22)·(23+24)

¿Cuáles fueron los cinco años anteriores con una relación similar? ¿Cuáles serán los cinco años siguientes?

• Escribimos la fecha de un día cualquiera del año con el formato “dd/mm/aa”, es decir, dos cifras para el día del mes, dos cifras para el mes y dos cifras para el año. ¿Qué días del año verifican “dd+mm=aa”? ¿Qué días del año verifican “dd·mm=aa”? ¿Qué días del año verifican “dd·mm·aa=2025”?

• Escribimos la hora, minutos y segundos de un instante de cualquier día del año con el formato “hh:mm:ss”, es decir, dos cifras para la hora, dos cifras para los minutos y dos cifras para los segundos. ¿Qué instantes de cada día verifican “hh·mm·ss=2025”?

• El año 2025 comienza y termina en miércoles. ¿Cuál fue el año anterior que empezó y terminó en miércoles? ¿Cuál será el año siguiente?

Las soluciones de las actividades las puedes encontrar en el siguiente enlace:

https://proyectodescartes.org/miscelanea/materiales_didacticos/Feliz_2025/index.html

OTRAS PROPIEDADES DEL NÚMERO 2025

Según los conjuntos numéricos que se estudian en la enseñanza de las Matemáticas, el número 2025 es un número natural, entero, racional y real. También se puede decir que es impar, múltiplo de 5, compuesto y cuadrado perfecto. En Matemáticas Recreativas aparecen otros tipos de números que verifican algunas propiedades curiosas y que reciben distintas denominaciones, llegando a ser contradictorias en algunos casos.

Según algunas de estas propiedades curiosas, se puede decir que el número 2025:

Es un número deficiente, la suma de sus divisores, excepto el mismo número, es menor que el número:

1+3+5+9+15+25+27+45+75+81+135+225+405+675 = 1726 < 2025

• Sin embargo, es un número poderoso porque es divisible por los cuadrados de cada uno de los factores primos que aparecen en su descomposición factorial.

Los factores primos que aparecen en la descomposición factorial de 2025 son 3 y 5. El número 2025 también es divisible por 3² y 5².

• Es un número infeliz, no se obtiene 1 al final de la secuencia de operaciones:

• Sin embargo, es un número que transmite alegría o número de Harshad, porque es divisible por la suma de sus cifras:

Pero, independientemente de lo que digan las Matemáticas de este número,

¡ Feliz 2025 !