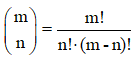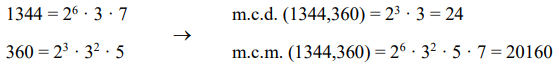Números

¡ FELIZ 2024 !

2024 = ( 21 + 23 ) · ( 22 + 24 )

• Descomposición factorial:     2024 = 2³ × 11 × 23

• El número 2024 se puede expresar como diferencia de cuadrados y, por tanto, como producto de una suma por una diferencia:

2024 = 2025 – 1 = 45² – 1² = (45-1)·(45+1) = 44·46

• Número de divisores: (3+1)·(1+1)·(1+1) = 4·2·2 = 16.

• Suma de sus cifras:     2 + 0 + 2 + 4 = 8

• Suma de los cuadrados de sus cifras:    2² + 0² + 2² + 4² = 24

• Operaciones curiosas con resultado 2024:   

2² + 4² + 6² + 8² + 10² + 12² + 14² + 16² + 18² + 20² + 22² = 2024

2³ + 3³ + 4³ + 5³ + 6³ + 7³ + 8³ + 9³ = 2024     

• El año 2024 es un año bisiesto. Son años bisiestos los múltiplos de 4, pero hay algunas excepciones. ¿Qué años son múltiplos de 4 y no son bisiestos?

• El número 2024 se escribe uniendo dos múltiplos de 4 consecutivos, 20 y 24. ¿Cuáles fueron los tres años anteriores a 2024 con esta propiedad? ¿Cuáles serán los tres años siguientes con esta propiedad? ¿Cada cuántos años sucede esto? ¿Por qué?

• La suma de las cifras del número 2024 es 8. ¿Cuáles fueron los cinco años anteriores a 2024 con esta propiedad? ¿Cuáles serán los cinco años siguientes con esta propiedad?

• La suma de los cuadrados de las cifras del número 2024 es 24. ¿Cuáles fueron los tres años anteriores a 2024 con esta propiedad? ¿Cuáles serán los tres años siguientes con esta propiedad?

• La suma de los cuadrados de las cifras del número 2024 coincide con las dos últimas cifras del número, 24. ¿Cuál fue el año anterior a 2024 con esta propiedad? ¿Cuál será el año siguiente con esta propiedad?

• El número 2024 se obtiene restando uno a un cuadrado perfecto 2024=2025–1=45²–1. ¿Cuáles fueron los tres años anteriores a 2024 con esta propiedad? ¿Cuáles serán los tres años siguientes con esta propiedad? ¿Cada cuántos años sucede esto?

• El número 2024 se puede expresar como el producto de dos números pares consecutivos, 2024=44·46. ¿Cuáles fueron los tres años anteriores a 2024 con esta propiedad? ¿Cuáles serán los tres años siguientes con esta propiedad? ¿Cada cuántos años sucede esto?

• Escribimos la fecha de un día cualquiera del año con el formato “dd/mm/aa”, es decir, dos cifras para el día del mes, dos cifras para el mes y dos cifras para el año. ¿Qué días del año verifican “dd+mm=aa”? ¿Qué días del año verifican “dd·mm=aa”?

• El año 2024 comienza en lunes y termina en martes. ¿Cuál será el próximo año que empiece en lunes y termine en martes?

Tiene 16 divisores: 1, 2, 4, 8, 11, 22, 23, 44, 46, 88, 92, 184, 253, 506, 1012 y 2024. Es un número abundante, la suma de sus divisores, excepto el mismo número, es mayor que el número:

1+2+4+8+11+22+23+44+46+88+92+184+253+506+1012 = 2296 > 2024

• Es un número infeliz, no se obtiene 1 al final de la secuencia de operaciones:

• Pero sin embargo es un número que transmite alegría o número de Harshad, porque es divisible por la suma de sus cifras:

Pero, independientemente de lo que digan las Matemáticas de este número,

¡ Feliz 2024 !

Un número es intocable es un número natural que no puede expresarse como la suma de los divisores propios de cualquier otro número o del mismo número.

Ejemplo: el número 7 no es intocable porque se obtiene sumando los divisores propios del número 8:

Div(8) = { 1 , 2 , 4 , 8 }  →  7 = 1 + 2 + 4

Son números intocables: 2, 5, 52, 88, 96, 120, 124, 146, 162, 188, 206, 210, 216, …

Un número es perfecto si la suma de todos sus divisores excepto él coincide con dicho número.

Si se suman todos los divisores, incluido el mismo número, un número perfecto verifica que la suma de todos sus divisores es igual al doble del número.

Un número es multiperfecto si la suma de todos los divisores, incluido el propio número, es igual a un múltiplo de dicho número. Según esta definición, los números perfectos también son biperfectos.

Ejemplo: el número 120 es triperfecto. La suma de sus divisores es:

1 + 2 + 3 + 4 + 5 + 6 + 8 + 10 + 12 + 15 + 20 + 24 + 30 + 40 + 60 + 120 = 360 = 3·120

Son números multiperfectos: 1, 6, 28, 120, 496, 672, 8128, 30240, 32760, 523776, …

Karl Friedrich Gauss (1777-1855) descubrió que cualquier número entero positivo se puede expresar como suma de, como máximo, tres números triangulares. Está relación la representó de la forma:

num = Δ + Δ + Δ 

Los primeros números triangulares son:  1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, 78, 91, 105, …

Por ejemplo:   100 = 3 + 6 + 91 = 1 + 21 + 78 = 6 + 28 + 66 = 45 + 55

Se llama factorial de un número natural n al producto de los n primeros números naturales. Se representa por n!.

Para el número 0 no tiene sentido esta definición. Se define factorial de 0 como 1. 0!=1. 

Se llama número combinatorio, m sobre n, con m≥n, a la expresión:

Si se colocan los números combinatorios formando el siguiente triángulo, conocido como triángulo de Pascal o triángulo de Tartaglia, se obtiene un método rápido para calcularlos. En este triángulo, cada número combinatorio se obtiene sumando los dos que tiene sobre él.

En el Triángulo se pueden comprobar las propiedades de los números combinatorios:

9. La suma de todos los números combinatorios que tienen como número superior m, es igual a 2^m.

10. Si en cada una de las filas del triángulo de Tartaglia, se alternan consecutivamente signos de sumar y restar, y se realizan las operaciones resultantes, el resultado es 0.

11. Sucesión de Fibonacci. Al sumar los números contenidos en cada una de las rectas se obtiene la sucesión de Fibonacci.

12. Binomio de Newton. Cada una de las filas del Triángulo de Pascal contiene todos los coeficientes del binomio de Newton (a+b)ⁿ.

Euclides (325-265 a.C.), en el séptimo libro de sus Elementos, describe el siguiente procedimiento para el cálculo del máximo común divisor, m.c.d., de dos números, conocido como Algoritmo de Euclides.

Se empieza dividiendo el número mayor entre el menor. Si se obtiene de resto 0, entonces el número menor es el m.c.d. de ambos. 

Si no se obtiene de resto 0, se divide el divisor de la división anterior entre el resto obtenido y se repite el mismo razonamiento hasta obtener una división exacta. 

Una vez que hayamos obtenido una división exacta, el divisor de la última división es el máximo común divisor de los dos números iniciales.

Ejemplo. Vamos a calcular el m.c.d. de los números 1344 y 360.

Se realizan las divisiones descritas anteriormente hasta obtener una división exacta:

El m.c.d. es el divisor de la última división:

m.c.d.(1344,360) = 24.

El mínimo común múltiplo se puede calcular con la relación:

Al calcular el m.c.d. y el m.c.m. con la descomposición factorial de los números, se obtiene:

Una curiosa e interesante propiedad de los números naturales. El cuadrado de la suma de los n primeros números naturales es igual a la suma de los cubos de dichos números.

( 1 + 2 + 3 + … + n )² = 1³ + 2³ + 3³ + … + n³

Comprobación para n=1, 2, 3, 4 y 5:

Demostración gráfica para n=4.

	La longitud del lado del cuadrado completo es: 1+2+3+4=10. El área del cuadrado completo es: (1+2+3+4)2=102=100.
	Hay un cuadrado de lado 1. Su área es 1.
	Juntando las dos mitades, hay dos cuadrados de lado 2. El área de los dos es 2·22=23.
	Hay tres cuadrados de lado 3. El área de los tres es 3·32=33.
	Juntando las dos mitades, hay cuatro cuadrados de lado 4. El área de los cuatro es 4·42=43.
	El área del cuadrado completo, sumando las área de todos los cuadrados es:  1·12+2·22+3·32+4·42=13+23+33+43=1+8+27+64=100.

¡ FELIZ 2023 !

¡ Un número que transmite alegría !

• Descomposición factorial:     2023 = 7 × 17 × 17 = 7 · 17²

• Suma de sus cifras:     2 + 0 + 2 + 3 = 7

• Suma de los cuadrados de sus cifras:    2² + 0² + 2² + 3² = 17

• Operaciones curiosas con resultado 2023:   

• La suma de las cifras del número 2023 es 7. ¿Cuáles fueron los tres años anteriores a 2023 con esta propiedad? ¿Cuáles serán los tres años siguientes con esta propiedad?

• La suma de los cuadrados de las cifras del número 2023 es 17. ¿Cuáles fueron los tres años anteriores a 2023 con esta propiedad? ¿Cuáles serán los tres años siguientes con esta propiedad?

• ¿Cuáles fueron los tres años anteriores a 2023 con las dos propiedades anteriores? ¿Cuáles serán los tres años siguientes con las dos propiedades?

• Escribimos la fecha de un día cualquiera del año con el formato “ddmmaa”, es decir, dos cifras para el día del mes, dos cifras para el mes y dos cifras para el año. ¿Qué días del año verifican “dd + mm = aa”? ¿Qué días del año verifican “dd · mm = aa”?

• El año 2023 comienza y termina en domingo, por lo que tendrá 53 domingos y 52 de cada uno de los demás días de la semana. ¿Cuál será el próximo año que empiece y termine en domingo? Cuidado con los años bisiestos.

• Si escribimos ahora la fecha de un día cualquiera del año con el formato “ddmmaaaa”, es decir, dos cifras para el día del mes, dos cifras para el mes y cuatro cifras para el año; ¿tiene este año alguna fecha capicúa (se lee igual de izquierda a derecha que de derecha a izquierda)? ¿Cuál fue la anterior fecha capicúa? ¿Cuál será la siguiente?

• Tiene 6 divisores: 1, 7, 17, 119, 289 y 2023. Es un número deficiente, la suma de sus divisores, excepto el mismo número, es menor que el número:

1 + 7 + 17 + 119 + 289 = 433 < 2023

• Es un número infeliz, no se obtiene 1 al final de la secuencia de operaciones:

• Pero sin embargo es un número que transmite alegría o número de Harshad, porque es divisible por la suma de sus cifras:

Pero, independientemente de lo que digan las Matemáticas de este número,

¡ Feliz 2023 !