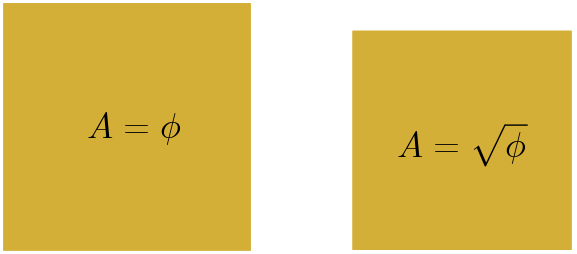Calendario Matemático SEMCV «Al Khwarizmi». 2025-26. Enero
La Sociedad de Educación Matemática de la Comunidad Valenciana «Al Khwarizmi» publica la quinta página de su Calendario Matemático anual, correspondiente al mes de enero del curso 2025-26. El problema de los días 26-27 corresponde a actividades de este blog.
Se puede acceder a la publicación haciendo «click» sobre la imagen siguiente.