En la Alhambra de Granada se pueden encontrar una gran cantidad de mosaicos extraordinarios.

En el suelo de la Sala del Mexuar encontramos este original enlosado construido con rectángulos y cuadrados.

Haz «click» sobre la imagen para comprobar, con una escena del Proyecto Descartes, como cambia el mosaico al modificar la relación entre los lados de los rectángulos. ¿Qué sucede para los valores 0 y 1?

Haz «click» sobre la imagen para comprobar, con GeoGebra, como cambia el mosaico al modificar la relación entre los lados de los rectángulos. ¿Qué sucede para los valores 0 y 1?

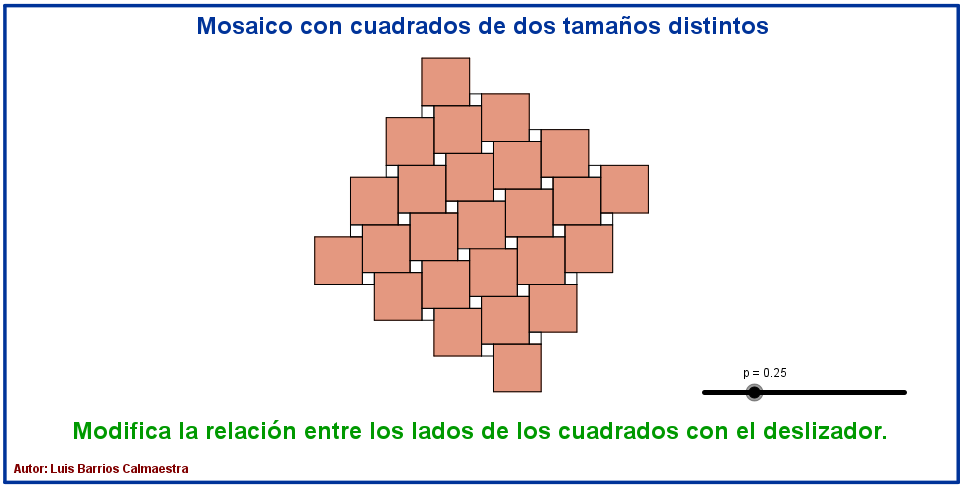
Un mosaico que se puede encontrar con facilidad en el embaldosado de edificios y calles es el formado por dos cuadrados de distinto tamaño.

En la primera imagen se puede observar un mosaico situado en la acera de la Avenida del Mediterráneo de Salobreña, en la provincia de Granada. En este mosaico, la longitud del lado del cuadrado menor es un cuarto de la longitud del lado del cuadrado mayor.

En la segunda imagen se puede observar un mosaico situado en una de las habitaciones de una Casa Típica del siglo XVIII de Guadalest, en la provincia de Alicante. En este mosaico, la longitud del lado del cuadrado menor es la mitad de la longitud del lado del cuadrado mayor.

Haz «click» sobre la imagen para comprobar, con una escena del Proyecto Descartes, como cambia el mosaico al modificar la relación entre los lados de los cuadrados. ¿Qué sucede para los valores 0 y 1?

Haz «click» sobre la imagen para comprobar, con GeoGebra, como cambia el mosaico al modificar la relación entre los lados de los cuadrados. ¿Qué sucede para los valores 0 y 1?

Paseando por la ciudad de Santander, observé en la acera de una de sus calles este curioso mosaico formado por rombos y cuadrados. 

Haz «click» sobre la imagen para comprobar, con una escena del Proyecto Descartes, como cambia el mosaico al modificar el ángulo menor del rombo. ¿Qué sucede para los valores 0º y 90º?

Haz «click» sobre la imagen para comprobar, con GeoGebra, como cambia el mosaico al modificar el ángulo menor del rombo. ¿Qué sucede para los valores 0º y 90º?

Publicación del libro digital interactivo «Deltoides con proporciones áureas«, dentro del proyecto iCartesiLibri de la Red Educativa Digital Descartes.

En este libro se estudia la existencia y construcción de deltoides con proporciones áureas. Se estudian deltoides convexos y cóncavos inscritos en un rectángulo áureo. Y se estudia también la existencia de deltoides que, aunque no están inscritos en un rectángulo de oro, verifican que sus lados y sus diagonales están en proporción áurea.

Se incluyen escenas interactivas del  Proyecto Descartes que ayudan a realizar la construcción paso a paso de las figuras estudiadas y a una mejor comprensión de sus propiedades. 

«Deltoides con proporciones áureas«

Publicación del libro digital interactivo «Cuadrados mágicos aditivos y multiplicativos«, dentro del proyecto iCartesiLibri de la Red Educativa Digital Descartes.

En este libro se exponen algunos de los cuadrados mágicos aditivos más conocidos, la forma de construirlos, sus propiedades y la forma de generar, a partir de ellos, otros cuadrados mágicos con las mismas características. También se explica como construir, a partir de los cuadrados mágicos aditivos, otros cuadrados mágicos multiplicativos con propiedades similares a los primeros. 

Para cada uno de los procedimientos de construcción descritos, se pueden construir una gran cantidad de ejemplos utilizando las escenas interactivas del Proyecto Descartes.

«Cuadrados mágicos aditivos y multiplicativos«

Información del Proyecto iCartesiLibri de la Red Educativa digital Descartes.

El objetivo de este proyecto es la conceptualización y el desarrollo de libros dinámicos, interactivos, multimedia, centrados en el aprendizaje y potenciadores de la educación de personas que aprenden a aprender, que adquieren autonomía y se forman competencialmente para afrontar su trayectoria vital.

Nuestro diseño hace que estos libros sean accesibles y plenamente operativos en cualquier ordenador personal o en cualquier dispositivo móvil tipo tableta y smartphone, independientemente del sistema operativo que porte.

Este espacio web se configura como un espacio evolutivo en el que las ideas fluyan a través de los ejemplares publicados, en el que la selección sea fruto del intercambio de experiencias y en el que los avances sean la sinergia de nuestra colaboración.

Un primer antecedente puede situarse en los libros interactivos del proyecto ED@D de la RED Descartes.

Todos estos libros incorporan escenas interactivas que usan DescartesJS.

https://proyectodescartes.org/iCartesiLibri/index.htm