Tangram triangular con Descartes JS
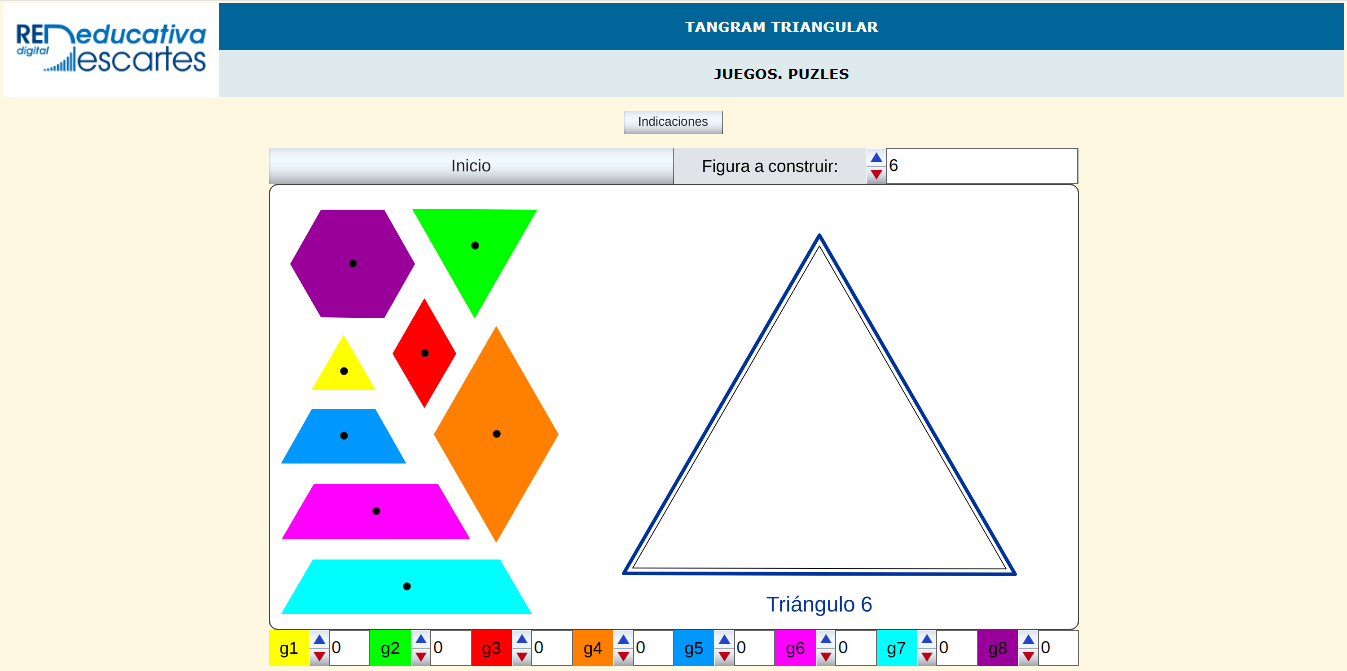
El tangram triangular es un rompecabezas compuesto por ocho piezas. Cada pieza se obtiene uniendo desde uno hasta ocho triángulos equiláteros.
Ya se ha presentado este puzle anteriormente en este blog realizado con GeoGebra. Ahora se plantea como una miscelánea del Proyecto Descartes.
Haz «click» sobre la imagen para abrir la miscelánea del Proyecto Descartes.